Biografie

Brahmagupta (598-668 CE)
De grote 7e-eeuwse Indiase wiskundige en astronoom Brahmagupta schreef enkele belangrijke werken over zowel wiskunde als astronomie. Hij was afkomstig uit de deelstaat Rajasthan in het noordwesten van India (hij wordt vaak aangeduid als Bhillamalacarya, de leraar van Bhillamala), en werd later het hoofd van het astronomisch observatorium in Ujjain in centraal India. De meeste van zijn werken zijn gecomponeerd in elliptische verzen, een gangbare praktijk in de Indiase wiskunde in die tijd, en hebben daardoor iets van een poëtische ring om hen.
Het lijkt waarschijnlijk dat Brahmagupta’s werken, in het bijzonder zijn meest beroemde tekst, de “Brahmasphutasiddhanta”, werden gebracht door de 8e eeuw Abbasid kalief Al-Mansur naar zijn nieuw opgerichte centrum van het leren in Bagdad aan de oevers van de Tigris, waardoor een belangrijke link tussen de Indiase wiskunde en astronomie en de ontluikende opleving in de wetenschap en wiskunde in de islamitische wereld.
In zijn werk over de rekenkunde legde Brahmagupta uit hoe men de kubus en de kubuswortel van een geheel getal kon vinden en gaf hij regels om de berekening van kwadraten en vierkantswortels te vergemakkelijken. Hij gaf ook regels voor het omgaan met vijf soorten combinaties van breuken. Hij gaf de som van de kwadraten van de eerste n natuurlijke getallen als n(n + 1)(2n + 1)⁄ 6 en de som van de kubussen van de eerste n natuurlijke getallen als (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Nul als getal behandelen

Brahmagupta’s regels voor het omgaan met nul en negatieve getallen
Brahmagupta’s genialiteit kwam echter tot uiting in zijn behandeling van het concept van het (toen betrekkelijk nieuwe) getal nul. Hoewel het vaak ook wordt toegeschreven aan de 7e-eeuwse Indiase wiskundige Bhaskara I, is zijn “Brahmasphutasiddhanta” waarschijnlijk de vroegst bekende tekst waarin het getal nul als een zelfstandig getal wordt behandeld, in plaats van als een gewoon plaatsvervangend cijfer zoals de Babyloniërs deden, of als een symbool voor een gebrek aan hoeveelheid zoals de Grieken en Romeinen deden.
Brahmagupta stelde de wiskundige basisregels vast voor het omgaan met nul (1 + 0 = 1; 1 – 0 = 1; en 1 x 0 = 0), hoewel zijn begrip van delen door nul onvolledig was (hij dacht dat 1 ÷ 0 = 0). Bijna 500 jaar later, in de 12e eeuw, toonde een andere Indiase wiskundige, Bhaskara II, aan dat het antwoord oneindig moest zijn, en niet nul (op grond van het feit dat 1 kan worden verdeeld in een oneindig aantal stukken van grootte nul), een antwoord dat eeuwenlang als juist werd beschouwd. Deze logica verklaart echter niet waarom 2 ÷ 0, 7 ÷ 0, enz., ook nul zouden moeten zijn – de moderne opvatting is dat een getal gedeeld door nul eigenlijk “ongedefinieerd” is (d.w.z. dat het geen zin heeft).
Brahmagupta’s opvatting van getallen als abstracte entiteiten, in plaats van alleen om te tellen en te meten, stelde hem in staat nog een andere grote conceptuele sprong te maken, die ingrijpende gevolgen zou hebben voor de toekomstige wiskunde. Tot dan toe werd de som 3 – 4, bijvoorbeeld, beschouwd als ofwel betekenisloos ofwel, in het beste geval, gewoon nul. Brahmagupta realiseerde zich echter dat er zoiets als een negatief getal kon bestaan, dat hij “schuld” noemde in tegenstelling tot “eigenschap”. Hij legde de regels uit voor het omgaan met negatieve getallen (b.v. een negatief maal een negatief is een positief, een negatief maal een positief is een negatief, etc).
Daarnaast wees hij erop dat kwadratische vergelijkingen (van het type x2 + 2 = 11, bijvoorbeeld) in theorie twee mogelijke oplossingen konden hebben, waarvan er één negatief kon zijn, omdat 32 = 9 en -32 = 9. Naast zijn werk aan oplossingen van algemene lineaire vergelijkingen en kwadratische vergelijkingen, ging Brahmagupta nog verder door stelsels van simultaanvergelijkingen (verzamelingen vergelijkingen die meerdere variabelen bevatten) te beschouwen, en kwadratische vergelijkingen met twee onbekenden op te lossen, iets wat in het Westen pas duizend jaar later werd overwogen, toen Fermat zich in 1657 over soortgelijke problemen boog.
Brahmagupta’s Stelling over cyclische vierhoeken
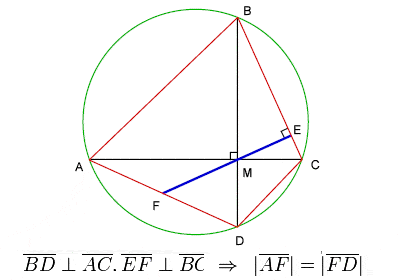
Brahmagupta’s Stelling over cyclische vierhoeken
Brahmagupta deed zelfs een poging om deze nogal abstracte concepten op te schrijven, Hij gebruikte de beginletters van de namen van kleuren om onbekenden in zijn vergelijkingen weer te geven, een van de vroegste aanzetten tot wat wij nu kennen als algebra.
Brahmagupta wijdde een aanzienlijk deel van zijn werk aan geometrie en trigonometrie. Hij stelde √10 (3,162277) vast als een goede praktische benadering voor π (3,141593), en gaf een formule, nu bekend als de Formule van Brahmagupta, voor de oppervlakte van een cyclische vierhoek, alsmede een gevierde stelling over de diagonalen van een cyclische vierhoek, meestal aangeduid als de Stelling van Brahmagupta.
| << Terug naar Indiase wiskunde | Voorwaarts naar Madhava >> |