Een cellulaire automaat is een verzameling “gekleurde” cellen op een raster met een bepaalde vorm dat zich in een aantal discrete tijdstappen ontwikkelt volgens een reeks regels die gebaseerd zijn op de toestanden van naburige cellen. De regels worden dan iteratief toegepast gedurende zoveel tijdstappen als gewenst. von Neumann was een van de eersten die een dergelijk model in overweging nam, en integreerde een cellulair model in zijn “universele constructor”. Cellulaire automaten werden bestudeerd in de vroege jaren 1950 als een mogelijk model voor biologische systemen (Wolfram 2002, p. 48). Uitgebreide studies van cellulaire automaten zijn uitgevoerd door S. Wolfram vanaf de jaren 1980, en Wolfram’s fundamentele onderzoek op het gebied culmineerde in de publicatie van zijn boek A New Kind of Science (Wolfram 2002), waarin Wolfram een gigantische verzameling van resultaten met betrekking tot automaten presenteert, waaronder een aantal baanbrekende nieuwe ontdekkingen.
In de aflevering van seizoen 2 “Bettor or Worse” (2006) van het tv-misdaaddrama NUMB3RS wordt melding gemaakt van eendimensionale cellulaire automaten.
Cellulaire automaten zijn er in een veelheid van vormen en variëteiten. Een van de meest fundamentele eigenschappen van een cellulaire automaat is het type rooster waarop hij wordt berekend. Het eenvoudigste “raster” is een eendimensionale lijn. In twee dimensies kunnen vierkante, driehoekige en zeshoekige roosters worden overwogen. Cellulaire automaten kunnen ook worden geconstrueerd op cartesische roosters in een willekeurig aantal dimensies, waarbij het 
-dimensionale gehele getallenrooster 
de meest voorkomende keuze is. Cellulaire automaten op een 
-dimensionaal geheel getalrooster zijn in de Wolfram Taal geïmplementeerd als CellularAutomaton.
Het aantal kleuren (of verschillende toestanden) 
dat een cellulaire automaat kan aannemen moet ook worden gespecificeerd. Dit aantal is meestal een geheel getal, waarbij 
(binair) de eenvoudigste keuze is. Voor een binaire automaat wordt kleur 0 gewoonlijk “wit” genoemd, en kleur 1 gewoonlijk “zwart”. Maar cellulaire automaten met een continu bereik van mogelijke waarden kunnen ook worden overwogen.
Naast het raster waarop een cellulaire automaat leeft en de kleuren die de cellen kunnen aannemen, moet ook de omgeving worden gespecificeerd waarin de cellen elkaar beïnvloeden. De eenvoudigste keuze is “naaste buren”, waarbij alleen cellen die direct grenzen aan een bepaalde cel bij elke tijdstap kunnen worden beïnvloed. Twee veel voorkomende buurgebieden in het geval van een tweedimensionale cellulaire automaat op een vierkant rooster zijn de zogenaamde Moore-buurt (een vierkante buurt) en de von Neumann-buurt (een ruitvormige buurt).
Het eenvoudigste type cellulaire automaat is een binaire, dichtstbijzijnde-buurt, eendimensionale automaat. Dergelijke automaten werden “elementaire cellulaire automaten” genoemd door S. Wolfram, die hun verbazingwekkende eigenschappen uitvoerig heeft bestudeerd (Wolfram 1983; 2002, p. 57). Er zijn 256 van dergelijke automaten, die elk kunnen worden geïndexeerd door een uniek binair getal waarvan de decimale voorstelling bekend is als de “regel” voor de automaat in kwestie. Een illustratie van regel 30 is hierboven afgebeeld samen met de evolutie die deze oplevert na 15 stappen uitgaande van een enkele zwarte cel.
Een iets gecompliceerdere klasse van cellulaire automaten zijn de dichtstbijzijnde-buurt, 
-kleur, eendimensionale totalistische cellulaire automaten. In dergelijke automaten is het gemiddelde van aangrenzende cellen bepalend voor de evolutie, en de eenvoudigste niet-triviale voorbeelden hebben 
kleuren. Voor deze automaten kan de reeks regels die het gedrag beschrijven, worden gecodeerd als een 
-cijferig 
-ary getal, bekend als een “code”. De regels en 300 stappen van de ternaire (
) code 912 automaat zijn hierboven geïllustreerd.
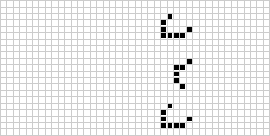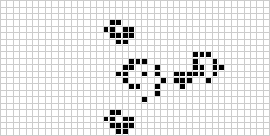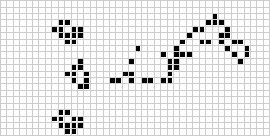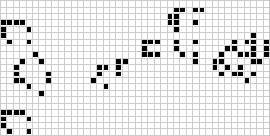
In twee dimensies is de bekendste cellulaire automaat Conway’s spel van het leven, ontdekt door J. H. Conway in 1970 en gepopulariseerd in de Scientific American columns van Martin Gardner. Het levensspel is een binaire (
) totalistische cellulaire automaat met een Moore buurt van bereik 
. Hoewel de berekening van de opeenvolgende generaties van het “game of life” oorspronkelijk met de hand werd gedaan, kwam al snel de computerrevolutie die het mogelijk maakte uitgebreidere patronen te bestuderen en te vermeerderen. Een animatie van de “game of life” constructie die bekend staat als een “puffer train” is hierboven afgebeeld.
WireWorld is een ander veel voorkomend tweedimensionaal cellulair automatisme.
De theorie van cellulaire automaten is immens rijk, met eenvoudige regels en structuren die in staat zijn een grote verscheidenheid van onverwachte gedragingen te produceren. Zo bestaan er bijvoorbeeld universele cellulaire automaten die in staat zijn het gedrag van elke andere cellulaire automaat of Turing machine te simuleren. Het is zelfs bewezen door Gacs (2001) dat er foutentolerante universele cellulaire automaten bestaan, waarvan het vermogen om andere cellulaire automaten te simuleren niet wordt gehinderd door willekeurige verstoringen, mits die verstoringen voldoende spaarzaam zijn.