Een verwarringsmatrix is een tabel die vaak wordt gebruikt om de prestaties van een classificatiemodel (of “classificator”) te beschrijven op een reeks testgegevens waarvan de werkelijke waarden bekend zijn. De verwarringsmatrix zelf is relatief eenvoudig te begrijpen, maar de bijbehorende terminologie kan verwarrend zijn.
Ik wilde een “quick reference guide” maken voor verwarringsmatrix-terminologie, omdat ik geen bestaande bron kon vinden die aan mijn eisen voldeed: compact in presentatie, met gebruik van getallen in plaats van willekeurige variabelen, en zowel uitgelegd in termen van formules als zinnen.
Laten we beginnen met een voorbeeld van een verwarringsmatrix voor een binaire classificator (hoewel deze gemakkelijk kan worden uitgebreid tot het geval van meer dan twee klassen):
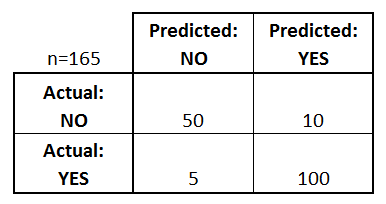
Wat kunnen we uit deze matrix leren?
- Er zijn twee mogelijke voorspelde klassen: “ja” en “nee”. Als we bijvoorbeeld de aanwezigheid van een ziekte voorspellen, zou “ja” betekenen dat ze de ziekte hebben, en “nee” dat ze de ziekte niet hebben.
- De classificator heeft in totaal 165 voorspellingen gedaan (bijv, 165 patiënten werden getest op de aanwezigheid van die ziekte).
- Van die 165 gevallen voorspelde de classificator 110 keer “ja”, en 55 keer “nee”.
- In werkelijkheid hebben 105 patiënten in de steekproef de ziekte, en 60 patiënten niet.
Laten we nu de meest elementaire termen definiëren, die gehele getallen zijn (geen percentages):
- ware positieven (TP): Dit zijn gevallen waarin we ja voorspelden (ze hebben de ziekte), en ze hebben de ziekte ook.
- ware negatieven (TN): We hebben nee voorspeld, en ze hebben de ziekte niet.
- vals positieven (FP): We voorspelden ja, maar ze hebben de ziekte in werkelijkheid niet. (Ook bekend als een “Type I-fout.”)
- vals-negatieven (FN): We voorspelden nee, maar ze hebben de ziekte in werkelijkheid wel. (Ook bekend als een “Type II-fout.”)
Ik heb deze termen toegevoegd aan de verwarringsmatrix, en ook de rij- en kolomtotalen toegevoegd:
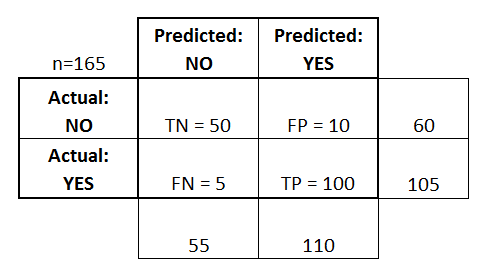
Dit is een lijst met percentages die vaak worden berekend uit een verwarringsmatrix voor een binaire classificator:
- Nauwkeurigheid: Hoe vaak is de classificator correct?
- (TP+TN)/totaal = (100+50)/165 = 0,91
- Misclassificatiegraad: Hoe vaak is het mis?
- (FP+FN)/totaal = (10+5)/165 = 0,09
- quivalent aan 1 min Accuracy
- ook bekend als “Error Rate”
- True Positive Rate: Als het echt ja is, hoe vaak voorspelt het dan ja?
- TP/werkelijk ja = 100/105 = 0,95
- ook bekend als “Sensitivity” of “Recall”
- False Positive Rate: Als het echt nee is, hoe vaak voorspelt het dan ja?
- FP/werkelijk nee = 10/60 = 0,17
- True Negative Rate: Wanneer het daadwerkelijk nee is, hoe vaak voorspelt het dan nee?
- TN/actueel nee = 50/60 = 0,83
- equivalent aan 1 min False Positive Rate
- ook bekend als “Specificiteit”
- Precisie: Als het ja voorspelt, hoe vaak is het dan juist?
- TP/voorspeld ja = 100/110 = 0,91
- Prevalentie: Hoe vaak komt de ja-voorwaarde daadwerkelijk voor in onze steekproef?
- werkelijke ja/totaal = 105/165 = 0,64
Een paar andere termen zijn ook het vermelden waard:
- Null Error Rate: Dit is hoe vaak je fout zou zitten als je altijd de meerderheidsklasse voorspelde. (In ons voorbeeld zou het nul-foutenpercentage 60/165=0.36 zijn, want als u altijd ja voorspelde, zou u alleen in de 60 “nee”-gevallen ongelijk hebben). Dit kan een nuttige basismaatstaf zijn om uw classificator mee te vergelijken. De beste classifier voor een bepaalde toepassing zal echter soms een hoger foutenpercentage hebben dan het nulfoutenpercentage, zoals blijkt uit de Accuracy Paradox.
- Cohen’s Kappa: Dit is in wezen een maatstaf voor hoe goed de classifier het heeft gedaan in vergelijking met hoe goed hij het gewoon bij toeval zou hebben gedaan. Met andere woorden, een model zal een hoge Kappa-score hebben als er een groot verschil is tussen de nauwkeurigheid en de nulfoutmarge. (Meer details over Cohen’s Kappa.)
- F Score: Dit is een gewogen gemiddelde van het waar-positieve percentage (recall) en de precisie. (Meer details over de F Score.)
- ROC Curve: Dit is een veelgebruikte grafiek die de prestaties van een classificator over alle mogelijke drempelwaarden samenvat. Zij wordt verkregen door de True Positive Rate (y-as) uit te zetten tegen de False Positive Rate (x-as) naarmate u de drempel voor de toewijzing van waarnemingen aan een bepaalde klasse varieert. (Meer details over ROC-curven.)
En tot slot, voor degenen onder u uit de wereld van de Bayesiaanse statistiek, hier is een korte samenvatting van deze termen uit Applied Predictive Modeling:
In relatie tot Bayesiaanse statistiek zijn de gevoeligheid en specificiteit de conditionele waarschijnlijkheden, de prevalentie is de prior, en de positieve/negatieve voorspelde waarden zijn de posterior waarschijnlijkheden.
Wilt u meer weten?
In mijn nieuwe video van 35 minuten, Making sense of the confusion matrix, ga ik dieper in op deze concepten en behandel ik meer geavanceerde onderwerpen:
- Hoe precisie en recall te berekenen voor multi-class problemen
- Hoe een 10-klassen verwarringsmatrix te analyseren
- Hoe de juiste evaluatiemethode te kiezen voor uw probleem
- Waarom nauwkeurigheid vaak een misleidende methode is
Laat het me weten als u vragen heeft!