Onbepaald lineair stelsel
Een onderbepaald stelsel van lineaire vergelijkingen heeft meer onbekenden dan vergelijkingen en heeft in het algemeen een oneindig aantal oplossingen. Onderstaande figuur toont zo’n vergelijkingssysteem y = D x {\displaystyle \mathbf {y} =D\mathbf {x} }

waarbij we een oplossing willen vinden voor x {\displaystyle \mathbf {x} } }

.
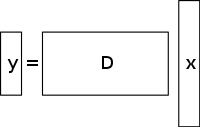
Om een oplossing voor zo’n systeem te kiezen, moet men extra beperkingen of voorwaarden (zoals gladheid) opleggen, al naar gelang het geval. Bij gecomprimeerde detectie voegt men de restrictie van sparsity toe, waardoor alleen oplossingen met een klein aantal niet-nul coëfficiënten zijn toegestaan. Niet alle ondergedetermineerde stelsels van lineaire vergelijkingen hebben een sparse oplossing. Indien er echter een unieke “sparse” oplossing voor het ondergedetermineerde stelsel bestaat, dan kan met behulp van “compressed sensing” deze oplossing worden gevonden.
Oplossing / reconstructie methode

Compressed sensing maakt gebruik van de redundantie in veel interessante signalen – het is geen zuivere ruis. In het bijzonder zijn veel signalen spaarzaam, d.w.z. dat zij veel coëfficiënten bevatten die dicht bij of gelijk aan nul zijn, wanneer zij in een bepaald domein worden weergegeven. Dit inzicht wordt ook gebruikt bij veel vormen van compressie met verlies.
Compressed sensing begint gewoonlijk met het nemen van een gewogen lineaire combinatie van monsters, ook wel compressieve metingen genoemd, in een andere basis dan de basis waarvan bekend is dat het signaal schaars is. De resultaten van Emmanuel Candès, Justin Romberg, Terence Tao en David Donoho hebben aangetoond dat het aantal van deze comprimerende metingen klein kan zijn en toch bijna alle nuttige informatie kan bevatten. Daarom moet bij de omzetting van het beeld naar het bedoelde domein een ondergedetermineerde matrixvergelijking worden opgelost, aangezien het aantal uitgevoerde comprimerende metingen kleiner is dan het aantal pixels in het volledige beeld. Door echter de beperking toe te voegen dat het initiële signaal schaars is, kan men dit onderbepaalde stelsel van lineaire vergelijkingen oplossen.
De kleinste-kwadraten-oplossing voor dergelijke problemen is het minimaliseren van de L 2 {\displaystyle L^{2}}

norm – dat wil zeggen, de hoeveelheid energie in het systeem minimaliseren. Dit is wiskundig meestal eenvoudig (het betreft slechts een matrixvermenigvuldiging met de pseudo-inverse van de basis waarin bemonsterd wordt). Dit leidt echter tot slechte resultaten voor veel praktische toepassingen, waarbij de onbekende coëfficiënten een energie hebben die niet nul is.
Om de sparsity constraint af te dwingen bij het oplossen van het ondergedetermineerde stelsel van lineaire vergelijkingen, kan men het aantal niet-nul componenten van de oplossing minimaliseren. De functie die het aantal niet-nul componenten van een vector telt, werd de L 0 {\displaystyle L^{0}}

“norm” genoemd door David Donoho.
Candès et al. bewezen dat het voor veel problemen waarschijnlijk is dat de L 1 {\displaystyle L^{1}}

norm gelijkwaardig is aan de L 0 {\displaystyle L^{0}}

norm, in technische zin: Dit gelijkwaardigheidsresultaat maakt het mogelijk om de L 1 {\displaystyle L^{1}}

op te lossen, wat gemakkelijker is dan het L 0 {\displaystyle L^{0}}

problem. Het vinden van de kandidaat met de kleinste L 1 {\displaystyle L^{1}}

norm kan betrekkelijk eenvoudig worden uitgedrukt als een lineair programma, waarvoor reeds efficiënte oplossingsmethoden bestaan. Wanneer de metingen een eindige hoeveelheid ruis kunnen bevatten, wordt de voorkeur gegeven aan denoising op basis van basisstreven boven lineaire programmering, omdat de sparsiteit bij ruis behouden blijft en het programma sneller kan worden opgelost dan een exact lineair programma.
Totale variatie gebaseerde CS-reconstructie
Motivatie en toepassingen
Rol van TV-regularisatie
Totale variatie kan worden gezien als een niet-negatieve reële-waarde functie gedefinieerd op de ruimte van reële-waarde functies (voor het geval van functies van één variabele) of op de ruimte van integreerbare functies (voor het geval van functies van meerdere variabelen). Voor signalen verwijst de totale variatie in het bijzonder naar de integraal van de absolute gradiënt van het signaal. Bij signaal- en beeldreconstructie wordt het toegepast als totale variatie regularisatie, waarbij het onderliggende principe is dat signalen met overmatige details een hoge totale variatie hebben en dat het verwijderen van deze details, met behoud van belangrijke informatie zoals randen, de totale variatie van het signaal zou verminderen en het signaalonderwerp dichter bij het oorspronkelijke signaal in het probleem zou brengen.
Voor signaal- en beeldreconstructie wordt l 1 {displaystyle l1}

minimalisatiemodellen worden gebruikt. Andere benaderingen zijn de kleinste-kwadratenmethode, die al eerder in dit artikel is besproken. Deze methoden zijn uiterst traag en leveren een niet-zo-perfecte reconstructie van het signaal op. De huidige CS-regularisatiemodellen trachten dit probleem aan te pakken door het inbouwen van sparsity priors van het oorspronkelijke beeld, waarvan er één de totale variatie (TV) is. Conventionele TV-benaderingen zijn ontworpen om stuk-voor-stuk constante oplossingen te geven. Enkele daarvan zijn (zoals verderop besproken) – constrained l1-minimization die gebruik maakt van een iteratief schema. Deze methode is weliswaar snel, maar leidt vervolgens tot een te sterke afvlakking van de randen, hetgeen resulteert in onscherpe beeldranden. TV-methoden met iteratieve herweging zijn toegepast om de invloed van grote gradiëntwaardemagnitudes in de beelden te verminderen. Dit is gebruikt bij de reconstructie van computertomografie (CT) als een methode die bekend staat als “edge-preserving total variation”. Aangezien de gradiëntmagnitudes echter worden gebruikt voor de raming van de relatieve strafgewichten tussen de betrouwbaarheid van de gegevens en de regularisatietermen, is deze methode niet robuust tegen ruis en artefacten en niet nauwkeurig genoeg voor CS-beeld/signaalreconstructie en slaagt er dus niet in kleinere structuren te behouden.
De recente vooruitgang met betrekking tot dit probleem behelst het gebruik van een iteratief directionele TV-verfijning voor CS-reconstructie. Deze methode bestaat uit twee fasen: in de eerste fase wordt het initiële oriëntatieveld geschat en verfijnd – dit veld wordt gedefinieerd als een ruisige punt-gewogen initiële schatting, door middel van rand-detectie, van het gegeven beeld. In de tweede fase wordt het CS-reconstructiemodel voorgesteld door gebruik te maken van directionele TV-regelaars. Meer details over deze op TV gebaseerde benaderingen – iteratief herwogen l1-minimalisatie, edge-preserving TV en iteratief model dat gebruik maakt van directioneel oriëntatieveld en TV – worden hieronder gegeven.
Bestaande benaderingen
Iteratief herwogen l1 {Displaystyle l_{1}}


minimalisatie

In de CS-reconstructiemodellen met gebruikmaking van constrained l 1 {{1}}

minimalisatie, worden grotere coëfficiënten zwaar bestraft in de l 1 {\displaystyle l_{1}}

norm. Voorgesteld werd om een gewogen formulering van l 1 {\displaystyle l_{1}}

minimalisatie te gebruiken om coëfficiënten die niet nul zijn op een meer democratische wijze te bestraffen. Er wordt een iteratief algoritme gebruikt om de juiste gewichten te construeren. Elke iteratie vereist het oplossen van één l 1 {\displaystyle l_{1}}

minimalisatieprobleem op door het lokale minimum te vinden van een concave straffunctie die meer lijkt op de l 0 {\displaystyle l_{0}}

norm. Een extra parameter, meestal om scherpe overgangen in de curve van de straffunctie te vermijden, wordt in de iteratieve vergelijking ingevoerd om de stabiliteit te waarborgen en zodat een nulschatting in de ene iteratie niet noodzakelijkerwijs leidt tot een nulschatting in de volgende iteratie. De methode houdt in wezen in dat de huidige oplossing wordt gebruikt voor de berekening van de gewichten die in de volgende iteratie moeten worden gebruikt.
Voordelen en nadelen
Bij vroege iteraties kunnen onnauwkeurige steekproefschattingen worden gevonden, maar bij deze methode zullen deze in een later stadium worden gedownsampled om meer gewicht te geven aan de kleinere niet-nul-schattingen van het signaal. Een van de nadelen is dat een geldig beginpunt moet worden bepaald, aangezien door de concaviteit van de functie niet altijd een globaal minimum zal worden bereikt. Een ander nadeel is dat deze methode de neiging heeft de beeldgradiënt uniform te bestraffen, ongeacht de onderliggende beeldstructuren. Dit leidt tot een te grote afvlakking van de randen, vooral die van gebieden met een laag contrast, waardoor informatie met een laag contrast verloren gaat. De voordelen van deze methode zijn: vermindering van de bemonsteringsfrequentie voor schaarse signalen; reconstructie van het beeld terwijl het robuust is voor het verwijderen van ruis en andere artefacten; en gebruik van zeer weinig iteraties. Dit kan ook helpen bij het herstellen van beelden met spaarzame gradiënten.
In de onderstaande figuur verwijst P1 naar de eerste stap van het iteratieve reconstructieproces, van de projectiematrix P van de geometrie van de fan-beam, die wordt begrensd door de data fidelity term. Deze kan ruis en artefacten bevatten, aangezien er geen regularisatie wordt uitgevoerd. De minimalisatie van P1 wordt opgelost met de geconjugeerde gradiëntmethode van de kleinste kwadraten. P2 verwijst naar de tweede stap van het iteratieve reconstructieproces, waarin gebruik wordt gemaakt van de randbehoudende totale variatie regularisatieterm om ruis en artefacten te verwijderen en zo de kwaliteit van het gereconstrueerde beeld/signaal te verbeteren. De minimalisering van P2 geschiedt met behulp van een eenvoudige gradiëntafdalingsmethode. De convergentie wordt bepaald door na elke iteratie te controleren of het beeld positief is, door na te gaan of f k – 1 = 0 {Displaystyle f^{k-1}=0}

voor het geval dat f k – 1 < 0 {\displaystyle f^{k-1}<0}

(Merk op dat f {\displaystyle f}

verwijst naar de verschillende lineaire verzwakkingscoëfficiënten van röntgenstraling in verschillende voxels van het patiëntenbeeld).
Edge-preserving total variation (TV) based compressed sensing

Dit is een iteratief CT-reconstructiealgoritme met edge-preserving TV-regularisatie om CT-beelden te reconstrueren van sterk undersampled gegevens die zijn verkregen bij CT met lage dosis door middel van lage stroomniveaus (milliampère). Om de beeldvormingsdosis te verminderen, wordt onder andere gebruik gemaakt van een vermindering van het aantal röntgenprojecties dat door de scannerdetectoren wordt verkregen. Deze onvoldoende projectiegegevens die worden gebruikt om het CT-beeld te reconstrueren, kunnen echter streperige artefacten veroorzaken. Bovendien leidt het gebruik van deze onvoldoende projecties in standaard TV-algoritmen ertoe dat het probleem ondergedetermineerd wordt en dus tot oneindig veel mogelijke oplossingen leidt. In deze methode wordt een extra gewogen straffunctie toegekend aan de oorspronkelijke TV-norm. Hierdoor kunnen scherpe discontinuïteiten in intensiteit in de beelden gemakkelijker worden gedetecteerd en kan het gewicht worden aangepast om de herstelde randinformatie op te slaan tijdens het proces van signaal/beeld-reconstructie. De parameter σ

regelt de mate van afvlakking die wordt toegepast op de pixels aan de randen om deze te onderscheiden van de niet-randpixels. De waarde van σ {{{\displaystyle \sigma }

wordt adaptief gewijzigd op basis van de waarden van het histogram van de gradiëntgrootte, zodat een bepaald percentage pixels gradiëntwaarden heeft die groter zijn dan σ {{displaystyle \sigma }

. De randbehoudende totale variatieterm wordt dus schaarser en dit versnelt de implementatie. Er wordt gebruik gemaakt van een tweestaps iteratieproces dat bekend staat als een voorwaarts-achterwaarts splitsingsalgoritme. Het optimalisatieprobleem wordt opgesplitst in twee subproblemen die vervolgens worden opgelost met respectievelijk de geconjugeerde gradiëntmethode met kleinste kwadraten en de eenvoudige gradiëntafdalingsmethode. De methode wordt gestopt wanneer de gewenste convergentie is bereikt of wanneer het maximumaantal iteraties is bereikt.
Voordelen en nadelen
Enige van de nadelen van deze methode zijn de afwezigheid van kleinere structuren in het gereconstrueerde beeld en degradatie van de beeldresolutie. Dit randbeschermende TV-algoritme vereist echter minder iteraties dan het conventionele TV-algoritme. Bij het analyseren van de horizontale en verticale intensiteitsprofielen van de gereconstrueerde beelden, kan men zien dat er scherpe sprongen zijn op randpunten en verwaarloosbare, kleine fluctuaties op niet-randpunten. Deze methode leidt dus tot een lage relatieve fout en een hogere correlatie in vergelijking met de TV-methode. Het onderdrukt en verwijdert ook effectief elke vorm van beeldruis en beeldartefacten zoals strepen.
Iteratief model dat gebruik maakt van een directioneel oriëntatieveld en directionele totale variatie
Om overmatig afvlakken van randen en textuurdetails te voorkomen en om een gereconstrueerd CS-beeld te verkrijgen dat nauwkeurig is en robuust voor ruis en artefacten, wordt deze methode gebruikt. Eerst wordt een eerste schatting gemaakt van het ruisige puntgerichte oriëntatieveld van het beeld I

, d ^ {{\displaystyle {d}}

, wordt verkregen. Dit ruis oriëntatieveld wordt gedefinieerd zodat het in een later stadium verfijnd kan worden om de ruis invloeden in de oriëntatieveld schatting te verminderen. Vervolgens wordt een grove oriëntatieveldschatting geïntroduceerd op basis van de structuurtensor die wordt geformuleerd als: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 22 ) {{ ∇ J_{\rho }(\nabla I_{\sigma })=G_{rho }*(\nabla I_{\sigma })={begin{pmatrix}J_{11}&J_{12}&J_{12}&J_22}}}

. Hierin is J ρ {{{{{{{{}}}}

verwijst naar de structuur tensor gerelateerd aan het beeld pixel punt (i,j) met standaardafwijking ρ {{\displaystyle J_{\rho }}}

. G {\displaystyle G}

verwijst naar de Gaussische kernel ( 0 , ρ 2 ) {\displaystyle (0,\rho ^{2})}

met standaardafwijking ρ {\displaystyle \rho }

. σ {\an8C↩sigma }

verwijst naar de handmatig gedefinieerde parameter voor de afbeelding I {{Displaystyle I}

waaronder de randdetectie ongevoelig is voor ruis. ∇ I σ {\displaystyle \nabla I_{\sigma }}

verwijst naar de gradiënt van het beeld I {\displaystyle I}

en ( ∇ I σ ⊗ ∇ I σ ) {\displaystyle (\nabla I_{sigma })}

verwijst naar het tensorproduct dat wordt verkregen door deze gradiënt te gebruiken.
De verkregen structuur tensor wordt geconvolveerd met een Gaussische kernel G {Displaystyle G}

om de nauwkeurigheid van de oriëntatieschatting te verbeteren met σ {\displaystyle \sigma }

worden ingesteld op hoge waarden om rekening te houden met onbekende ruisniveaus. Voor elke pixel (i,j) in het beeld is de structuurtensor J een symmetrische en positieve half-eindige matrix. Convolving van alle pixels in het beeld met G {Displaystyle G}

, geeft orthonormale eigenvectoren ω en υ van de J {{\displaystyle J}

matrix. ω wijst in de richting van de dominante oriëntatie met het grootste contrast en υ wijst in de richting van de structuuroriëntatie met het kleinste contrast. Het oriëntatieveld grove initiële schatting d ^ {\displaystyle {d}}

is gedefinieerd als d ^ {{\displaystyle {\hat {d}}}

= υ. Deze schatting is nauwkeurig bij sterke randen. Maar bij zwakke randen of in gebieden met ruis neemt de betrouwbaarheid af.
Om dit nadeel te ondervangen wordt een verfijnd oriëntatiemodel gedefinieerd waarin de gegevensterm het effect van ruis vermindert en de nauwkeurigheid verbetert, terwijl de tweede strafterm met de L2-norm een getrouwheidsterm is die de nauwkeurigheid van de aanvankelijke grove schatting garandeert.
Dit oriëntatieveld wordt ingevoerd in het directionele totale variatie-optimalisatiemodel voor CS-reconstructie door middel van de vergelijking m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}} \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}

. X {\mathrm {X}}

is het objectieve signaal dat moet worden teruggewonnen. Y is de overeenkomstige meetvector, d is het iteratief verfijnde oriëntatieveld en Φ {Phi}

is de benaderde schatting van het oriëntatieveld van het gereconstrueerde beeld X k – 1 {\displaystyle X^{k-1}}

van de vorige iteratie (om de convergentie en de daaropvolgende optische prestaties te controleren, wordt de vorige iteratie gebruikt). Voor de twee vectorvelden die worden weergegeven door X {\displaystyle \mathrm {X} }

en d {\displaystyle d}

, X ∙ d {\displaystyle \mathrm {X} \bullet d}

verwijst naar de vermenigvuldiging van de respectieve horizontale en verticale vectorelementen van X {\displaystyle \mathrm {X} }

en d {{\displaystyle d}

gevolgd door hun latere optelling. Deze vergelijkingen worden gereduceerd tot een reeks convexe minimalisatieproblemen die vervolgens worden opgelost met een combinatie van variabele splitsing en augmented Lagrangian (op FFT gebaseerde snelle oplosser met een gesloten vorm oplossing) methoden. Deze methode (Augmented Lagrangian) wordt beschouwd als equivalent van de gesplitste Bregman iteratie die de convergentie van deze methode garandeert. Het oriëntatieveld, d wordt gedefinieerd als zijnde gelijk aan ( d h , d v ) {displaystyle (d_{h},d_{v})}

, waarbij d h , d v {\displaystyle d_{h},d_{v}}

de horizontale en verticale schattingen van d {\displaystyle d}

.

De Augmented Lagrangian method for the orientation field, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\displaystyle min_{\mathrm {X} }\lVert \nabla \mathrm {X} \bullet d\rVert _{1}+{\frac {\lambda }{2}} \lVert Y-\Phi \mathrm {X} \rVert _{2}^{2}}

, impliceert het initialiseren van d h , d v , H , V {\displaystyle d_{h},d_{v},H,V}

en vervolgens de benaderde minimizer van L 1 {\displaystyle L_{1}}

met betrekking tot deze variabelen. De Lagrangiaanse vermenigvuldigers worden vervolgens bijgewerkt en het iteratieve proces wordt gestopt wanneer convergentie is bereikt. Voor het iteratieve directionele totale-variatie-verfijningsmodel houdt de augmented lagrangian methode in dat X , P , Q , λ P , λ Q worden geïnitialiseerd {\displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}

.
Hier, H , V , P , Q {\displaystyle H,V,P,Q}

zijn nieuw ingevoerde variabelen waarbij H {\displaystyle H}

= ∇ d h {\displaystyle d_{h}}

= ∇ d v {\displaystyle \nabla d_{v}}

, P {{v}

= ∇ X {\anabla \mathrm {X}}

, en Q {{\displaystyle Q}

= P ∙ d {{Displaystyle P}

. λ H , λ V , λ P , λ Q {\displaystyle \lambda _{H},\lambda _{V},\lambda _{P},\lambda _{Q}}

zijn de Lagrangiaanse vermenigvuldigingsfactoren voor H , V , P , Q {\displaystyle H,V,P,Q}

. Voor elke iteratie wordt de benaderde minimizer van L 2 {\displaystyle L_{2}}

met betrekking tot de variabelen ( X , P , Q {\displaystyle \mathrm {X} ,P,Q}

) wordt berekend. En net als in het veldverfijningsmodel worden de lagrangiaanse vermenigvuldigers bijgewerkt en wordt het iteratieve proces gestopt wanneer convergentie is bereikt.
Voor het oriëntatieveld-verfijningsmodel worden de Lagrangiaanse multiplicatoren in het iteratieve proces als volgt geactualiseerd:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) {\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}.

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) {\displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Voor het iteratieve directionele totale variatie verfijningsmodel worden de Lagrangiaanse vermenigvuldigers als volgt geactualiseerd:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\displaystyle (\lambda _{P})^{k}=(\lambda _{P})^{k-1}+\gamma _{P}(P^{k}-\nabla (\mathrm {X} )^{k})}.

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) {displaystyle (\lambda _{Q})^{k}=(\lambda _{Q})^{k-1}+\gamma _{Q}}(Q^{k}-P^{k}})}

Hierbij, γ H , γ V , γ P , γ Q {Displaystyle γgamma _{H},γgamma _{V},γgamma _{P},γgamma _{Q}}

zijn positieve constanten.
Voordelen en nadelen
Op basis van de piek signaal-ruisverhouding (PSNR) en de structurele gelijksoortigheidsindex (SSIM) en op basis van bekende ground-truth beelden voor het testen van de prestaties, wordt geconcludeerd dat de iteratieve directionele totale variatie een betere gereconstrueerde prestatie heeft dan de niet-iteratieve methoden voor het behoud van rand- en textuurgebieden. Het oriëntatieveld verfijningsmodel speelt een belangrijke rol in deze prestatieverbetering omdat het het aantal richtingloze pixels in het vlakke gebied verhoogt terwijl het de consistentie van het oriëntatieveld in de gebieden met randen verbetert.