Leerdoel
1. Omzetten van een eenheid naar een andere eenheid van hetzelfde type.
In Paragraaf 2.2 “Eenheden uitdrukken”, hebben we enkele voorbeelden laten zien van hoe je initiële eenheden kunt vervangen door andere eenheden van hetzelfde type om een numerieke waarde te krijgen die gemakkelijker te begrijpen is. In deze paragraaf zullen we het proces formaliseren.
Neem een eenvoudig voorbeeld: hoeveel voet is er in 4 yards? De meeste mensen zullen bijna automatisch antwoorden dat er 12 voet in 4 yards zit. Hoe komt u tot deze vaststelling? Wel, als er 3 voet in 1 yard is en er zijn 4 yards, dan zijn er 4 × 3 = 12 voet in 4 yards.
Dit is correct, natuurlijk, maar het is informeel. Laten we het formaliseren op een manier die meer algemeen kan worden toegepast. We weten dat 1 yard (yd) gelijk is aan 3 feet (ft):
1 yd = 3 ft
In de wiskunde wordt deze uitdrukking een gelijkheid genoemd. De regels van de algebra zeggen dat je de gelijkheid kunt veranderen (d.w.z. vermenigvuldigen of delen of optellen of aftrekken) zolang je niet door nul deelt en de nieuwe uitdrukking nog steeds een gelijkheid zal zijn. Als we bijvoorbeeld beide zijden door 2 delen, krijgen we
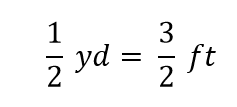
We zien dat de helft van een yard gelijk is aan 3/2, of anderhalve feet – iets waarvan we ook weten dat het waar is, dus de bovenstaande vergelijking is nog steeds een gelijkheid. Terug naar de oorspronkelijke gelijkheid, stel dat we beide kanten van de vergelijking delen door 1 yard (getal en eenheid):
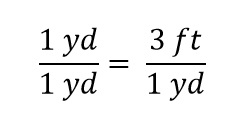
De uitdrukking is nog steeds een gelijkheid, volgens de regels van de algebra. De linker breuk is gelijk aan 1. Ze heeft dezelfde hoeveelheid in de teller en in de noemer, dus moet ze gelijk zijn aan 1. De hoeveelheden in de teller en de noemer heffen elkaar op, zowel het getal als de eenheid:
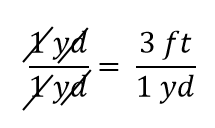
Wanneer alles in een breuk elkaar opheft, wordt de breuk 1:
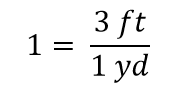
We hebben een uitdrukking, 3 ft1 yd, die gelijk is aan 1. Dit is een vreemde manier om 1 te schrijven, maar het is logisch: 3 ft is gelijk aan 1 yd, dus de hoeveelheden in de teller en de noemer zijn dezelfde hoeveelheid, alleen uitgedrukt in verschillende eenheden. De uitdrukking 3 ft1 yd heet een conversiefactor, en wordt gebruikt om de eenheid van een grootheid formeel te veranderen in een andere eenheid. (Het proces van omrekenen van eenheden op zo’n formele manier wordt ook wel dimensionale analyse of de factorlabelmethode genoemd.)
Om te zien hoe dit gebeurt, beginnen we met de oorspronkelijke grootheid:
4 yd
Nu vermenigvuldigen we deze grootheid met 1. Wanneer je iets met 1 vermenigvuldigt, verander je de waarde van de grootheid niet. In plaats van te vermenigvuldigen met 1, schrijven we 1 als 3 ft1 yd:
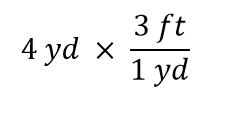
De term 4 yd kan worden opgevat als 4 yd/1; dat wil zeggen, het kan worden opgevat als een breuk met 1 in de noemer. We zijn in wezen breuken aan het vermenigvuldigen. Als hetzelfde voorkomt in de teller en de noemer van een breuk, dan heffen ze elkaar op. In dit geval heffen we de yard op:
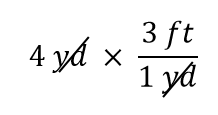
Dat is alles wat we kunnen heffen. Nu vermenigvuldigen en delen we alle getallen om het uiteindelijke antwoord te krijgen: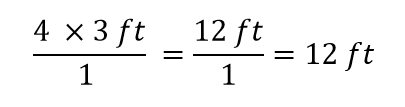
Wederom krijgen we een antwoord van 12 ft, net zoals we oorspronkelijk deden. Maar in dit geval hebben we een formelere procedure gebruikt die op allerlei problemen van toepassing is.
Hoeveel millimeters zitten er in 14,66 m? Om dit te beantwoorden, moeten we een omrekeningsfactor tussen millimeters en meters construeren en die correct toepassen op de oorspronkelijke grootheid. We beginnen met de definitie van een millimeter, en die is
1 mm = 1/1.000 m
De 1/1.000 is wat het voorvoegsel milli- betekent. De meeste mensen vinden het prettiger om zonder breuken te werken, dus zullen we deze vergelijking herschrijven door de 1.000 in de teller van de andere kant van de vergelijking te brengen:
1.000 mm = 1 m
Nu construeren we een omrekeningsfactor door één grootheid door beide kanten te delen. Maar nu rijst de vraag: door welke grootheid delen we? Het blijkt dat we twee keuzes hebben, en de twee keuzes geven ons verschillende conversiefactoren, die beide gelijk zijn aan 1:
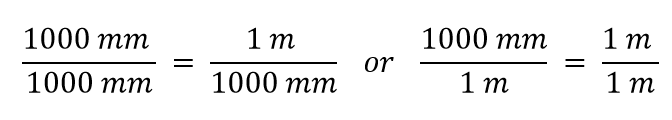
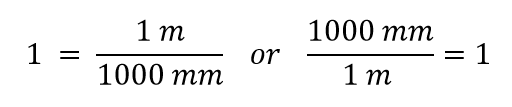
Welke conversiefactor gebruiken we? Het antwoord is gebaseerd op de eenheid die u wilt weglaten in uw oorspronkelijke hoeveelheid. De oorspronkelijke eenheid van onze hoeveelheid is meters, die we willen omrekenen naar millimeters. Omdat de oorspronkelijke eenheid in de teller wordt verondersteld te staan, willen we de eenheid van meter in de noemer; dan heffen ze elkaar op. Daarom gebruiken we de tweede conversiefactor. Door de eenheden te annuleren en de wiskunde uit te voeren, krijgen we
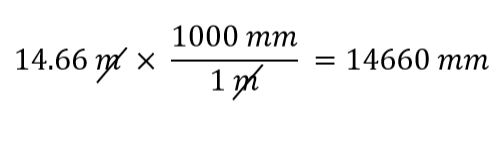
Zie hoe m annuleert, zodat mm overblijft, de eenheid waar het om gaat.
Het vermogen om de juiste conversiefactoren te construeren en toe te passen, is een zeer krachtige wiskundige techniek in de scheikunde. Je moet deze techniek beheersen als je succesvol wilt zijn in deze en toekomstige cursussen.
Voorbeeld 7
- Verander 35,9 kL in liters.
- Verander 555 nm in meters.
Oplossing
-
We zullen gebruik maken van het feit dat 1 kL = 1.000 L. Van de twee omrekeningsfactoren die kunnen worden gedefinieerd, is de factor die zal werken 1.000 L/1 kL. Als we deze omrekeningsfactor toepassen, krijgen we
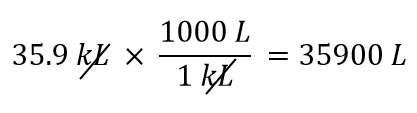
-
We zullen het feit gebruiken dat 1 nm = 1/1.000.000.000 m, wat we zullen herschrijven als 1.000.000.000 nm = 1 m, of 109 nm = 1 m. Van de twee mogelijke omrekeningsfactoren, heeft de juiste de eenheid nm in de noemer: 1 m/109 nm. Als we deze omrekeningsfactor toepassen, krijgen we
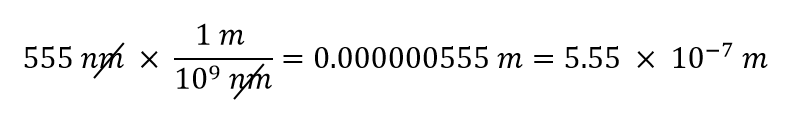
In de laatste stap hebben we het antwoord in wetenschappelijke notatie uitgedrukt.
Test jezelf
- Omrekenen 67.08 μL omrekenen naar liters.
- 56,8 m omrekenen naar kilometers.
Answers
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Wat als we een afgeleide eenheid hebben die het product is van meer dan één eenheid, zoals m2? Stel dat we vierkante meters willen omrekenen naar vierkante centimeters? De sleutel is om te onthouden dat m2 betekent m × m, wat betekent dat we twee meter eenheden hebben in onze afgeleide eenheid. Dat betekent dat we twee conversiefactoren moeten opnemen, één voor elke eenheid. Om bijvoorbeeld 17,6 m2 om te rekenen naar vierkante centimeters, doen we dat als volgt:
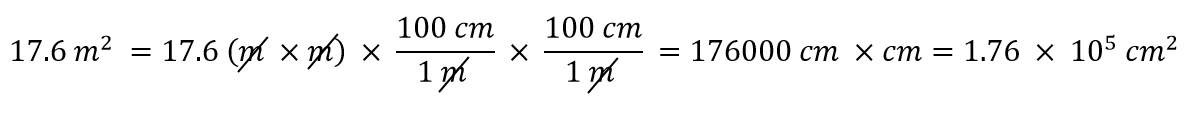
Voorbeeld 8
Hoeveel kubieke centimeters zitten er in 0.883 m3?
Oplossing
Met een exponent van 3 hebben we drie lengte-eenheden, dus bij uitbreiding moeten we drie conversiefactoren gebruiken tussen meters en centimeters. Zo hebben we
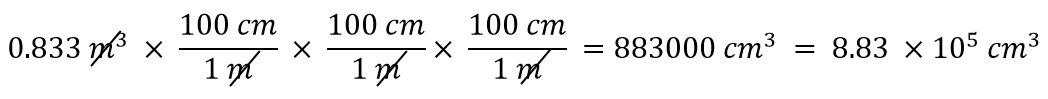
U moet voor uzelf aantonen dat de drie meter-eenheden inderdaad opheffen.
Test jezelf
Hoeveel kubieke millimeters zitten er in 0,0923 m3?
Antwoord
9,23 × 107 mm3
Stel dat de eenheid die je wilt omrekenen in de noemer van een afgeleide eenheid staat; wat dan? Dan moet in de omrekeningsfactor de eenheid die je wilt schrappen in de teller staan. Dit zal de oorspronkelijke eenheid in de noemer opheffen en een nieuwe eenheid in de noemer introduceren. Het volgende voorbeeld illustreert deze situatie.
Voorbeeld 9
Verander 88,4 m/min in meter/seconde.
Oplossing
We willen de eenheid in de noemer veranderen van minuten in seconden. Omdat er 60 seconden in 1 minuut zitten (60 s = 1 min), construeren we een conversiefactor zodat de eenheid die we willen weghalen, minuten, in de teller komt te staan: 1 min/60 s. Pas toe en voer de wiskunde uit:
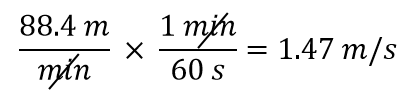
Merk op hoe de 88,4 automatisch in de teller komt te staan. Dat komt omdat elk getal in de teller van een breuk gedeeld door 1 kan staan.
Test jezelf
Omrekenen van 0,203 m/min naar meter/seconde.
Antwoord
0.00338 m/s of 3,38 × 10-3 m/s
Figuur 2.8 Hoe snel is snel?

Bron: “Grapevine snail” door Jürgen Schoneris onder de Creative Commons Naamsvermelding-Gelijk delen-licentie 3.0 Unported.