Samendrukbaarheidsfactor (gassen) - Knowino

Van Knowino

Dit is een gecontroleerde versie van deze pagina

Jump to: navigatie,zoeken

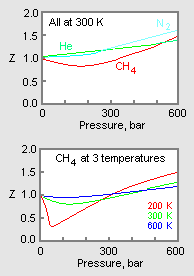
Figuur 1: Voorbeeldgrafieken van samendrukbaarheidsfactoren van gassen

De samendrukbaarheidsfactor (Z) is een nuttige thermodynamische eigenschap om de ideale gaswet aan te passen aan het gedrag van echte gassen. Het is een maat voor de mate waarin de thermodynamische eigenschappen van een reëel gas afwijken van die welke van een ideaal gas worden verwacht. Zij kan worden beschouwd als de verhouding van het werkelijke volume van een reëel gas tot het volume dat door het ideale gas wordt voorspeld bij dezelfde temperatuur en druk als het werkelijke volume.

Voor een ideaal gas heeft Z altijd een waarde van 1. Voor echte gassen kan de waarde positief of negatief afwijken, afhankelijk van het effect van de intermoleculaire krachten van het gas. Hoe dichter een reëel gas zich bij zijn kritische punt of bij zijn verzadigingspunt bevindt, des te groter zijn de afwijkingen van het gas ten opzichte van het ideale gedrag.

De bovenste grafiek in figuur 1 illustreert hoe de samendrukbaarheidsfactor varieert voor verschillende gassen bij eenzelfde temperatuur en druk. De onderste grafiek illustreert hoe de samendrukbaarheidsfactor van een gas (bijvoorbeeld methaan) bij een gegeven druk varieert met de temperatuur.

Dit artikel behandelt alleen de samendrukbaarheidsfactor van gassen en gaat niet in op de samendrukbaarheid van vloeistoffen of damp-vloeistofmengsels.

Inhoud

1 Bepaling van de samendrukbaarheidswaarden van gassen

1.1 Veralgemeende samendrukbaarheidsfactorgrafieken voor zuivere gassen
1.2 Veralgemeende samendrukbaarheidsfactorgrafieken voor gasmengsels
1.3 De van der Waals-vergelijking
- 1.3.1 Gewijzigde versies van de van der Waals-vergelijking
  - 1.3.1.1 Redlich-Kwong
  - 1.3.1.2 Soave-Redlich-Kwong
  - 1.3.1.3 Peng-Robinson
1.4 Viriale toestandsvergelijking
1.5 Andere toestandsvergelijkingen

1.5 De vergelijking van de gasconstante

1.5.1.3 Peng-Robinson
- 1.5.6 Notatie voor de gasconstante
2 Referenties

Bepaling van de samendrukbaarheidswaarden van gassen

De ideale gaswet is gedefinieerd als:

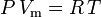
$P\,V_\mathrm{m} = RR\,T$

en de ideale gaswet gecorrigeerd voor niet-idealiteit is gedefinieerd als:

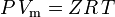
$P\,V_\mathrm{m} = ZR\,T$

waar:
P	= druk
Vm	= molair volume van het gas
Z	= samendrukbaarheidsfactor
R	= universele gasconstante
T	= temperatuur

en dus:

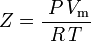
$Z = \frac{;P,V_mathrm{m}}{R\,T}$

dat is de eenvoudigste en meest gebruikte toestandsvergelijking (EOS) voor echte gassen. De belangrijkste beperking van deze toestandsvergelijking is dat de samendrukbaarheidsfactor van het gas, Z, geen constante is, maar varieert van gas tot gas en met de temperatuur en de druk van het beschouwde gas. Hij moet experimenteel worden bepaald.

Wanneer experimentele gegevens beschikbaar zijn voor specifieke gassen, kunnen die gegevens worden gebruikt om grafieken te maken (zoals in figuur 1) van Z tegen druk bij een constante temperatuur of van Z tegen druk voor verschillende temperaturen voor die specifieke gassen. Dergelijke grafieken zijn nuttig voor het gemakkelijk verkrijgen van geïnterpoleerde waarden van Z tussen de experimenteel bepaalde waarden.

De samendrukbaarheidsfactor kan, zoals eerder vermeld, ook worden uitgedrukt als:

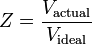
$Z = \frac{V_\mathrm{actueel}}{V_\mathrm{ideaal}}$

Er zijn drie regimes die de samendrukbaarheidsfactor beïnvloeden:

de waarde van Z neigt naar 1 naarmate de gasdruk dichter bij 0 komt, waarbij alle gassen neigen naar ideaal gedrag
de waarde van Z is kleiner dan 1 bij intermediaire drukken omdat de intermoleculaire aantrekkingskrachten de werkelijke volumes kleiner doen zijn dan de ideale waarden
de waarde van Z is groter dan 1 en neigt uiteindelijk naar oneindig bij hoge druk omdat de intermoleculaire afstotingskrachten de werkelijke volumes groter doen zijn dan de ideale waarden

Gegeneraliseerde samendrukbaarheidsfactor-grafieken voor zuivere gassen

De unieke relatie tussen de samendrukbaarheidsfactor en de gereduceerde temperatuur, Tr, en de gereduceerde druk, Pr, werd voor het eerst erkend door van der Waals in 1873 en staat bekend als het twee-parameter principe van overeenkomstige toestanden. Het principe van overeenkomstige toestanden drukt de veralgemening uit dat de eigenschappen van een gas die afhankelijk zijn van intermoleculaire krachten, op universele wijze in verband staan met de kritische eigenschappen van het gas. Dat verschaft een zeer belangrijke basis voor het ontwikkelen van correlaties van moleculaire eigenschappen.

Wat de samendrukbaarheid van gassen betreft, geeft het principe van overeenkomstige toestanden aan dat elk zuiver gas bij dezelfde gereduceerde temperatuur, Tr, en gereduceerde druk, Pr, dezelfde samendrukbaarheidsfactor moet hebben.

De gereduceerde temperatuur en druk zijn gedefinieerd als:

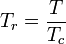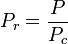
$T_r = \frac{T}{T_c}$ en $P_r = \frac{P}{P_c}$

Tc en Pc staan bekend als de kritische temperatuur en de kritische druk van een gas. Zij zijn karakteristieken van elk specifiek gas, waarbij Tc de temperatuur is waarboven het niet mogelijk is een bepaald gas vloeibaar te maken en Pc de minimumdruk is die vereist is om een bepaald gas bij zijn kritische temperatuur vloeibaar te maken. Samen definiëren zij het kritieke punt van een vloeistof waarboven afzonderlijke vloeibare en gasvormige fasen van een bepaalde vloeistof niet bestaan.

De druk-volume-temperatuur (PVT) gegevens voor echte gassen variëren van het ene zuivere gas tot het andere. Wanneer echter de samendrukbaarheidsfactoren van verschillende gassen met één component worden uitgezet tegen de druk, samen met de temperatuur-isothermen (zoals voor methaan in de onderste grafiek van figuur 1), vertonen veel van de grafieken soortgelijke isothermvormen.

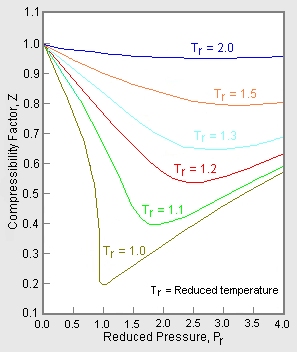
Figuur 2: Voorbeeld van een gegeneraliseerde drukbaarheidsfactor-grafiek

Om een gegeneraliseerde grafiek te verkrijgen die voor veel verschillende gassen kan worden gebruikt, worden de verlaagde druk en temperatuur, Pr en Tr, gebruikt om de gegevens van de drukbaarheidsfactor te normaliseren. Figuur 2 is een voorbeeld van een gegeneraliseerde samendrukbaarheidsfactor-grafiek, afgeleid uit honderden experimentele P-V-T-gegevenspunten van 10 zuivere gassen, namelijk methaan, ethaan, ethyleen, propaan, n-butaan, i-pentaan, n-hexaan, stikstof, kooldioxide en stoom.

Er zijn meer gedetailleerde gegeneraliseerde samendrukbaarheidsfactor-grafieken, gebaseerd op wel 25 of meer verschillende zuivere gassen, zoals de Nelson-Obert-grafieken. Dergelijke grafieken hebben naar verluidt een nauwkeurigheid binnen 1-2 procent voor Z-waarden groter dan 0,6 en binnen 4-6 procent voor Z-waarden van 0,3-0,6.

De gegeneraliseerde samendrukbaarheidsfactor-grafieken kunnen een aanzienlijke fout vertonen voor sterk polaire gassen, d.w.z. gassen waarvan de centra van positieve en negatieve lading niet samenvallen. In dergelijke gevallen kan de schatting voor Z een fout vertonen die kan oplopen tot 15-20 procent.

De kwantumgassen waterstof, helium en neon voldoen niet aan het gedrag van de overeenkomstige toestanden en de gereduceerde druk en temperatuur voor deze drie gassen moeten op de volgende wijze worden geherdefinieerd om de nauwkeurigheid van de voorspelling van hun samendrukbaarheidsfactoren bij gebruik van de gegeneraliseerde grafieken te verbeteren:

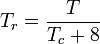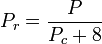
$T_r = \frac{T}{T_c + 8}$ en $P_r = \frac{P}{P_c + 8}$

waarbij de temperaturen in graden Kelvin zijn en de drukken in atmosferen.

Gegeneraliseerde samendrukbaarheidsfactor-grafieken voor gasmengsels

De gegeneraliseerde samendrukbaarheidsfactor-grafieken voor zuivere gassen (zoals geïllustreerd in figuur 2 of de Nelson-Obert-grafieken kunnen ook worden gebruikt voor gasmengsels door gebruik te maken van de regel van Kay die in 1936 door W. B. Kay werd voorgesteld. Deze regel voorspelt het P-V-T gedrag van een gasmengsel door de samendrukbaarheidsfactor te bepalen voor een gasmengsel bij verlaagde temperatuur en verlaagde druk, gedefinieerd in termen van de pseudokritische temperatuur, Tpc en de pseudokritische druk, Ppc, die worden gedefinieerd als:

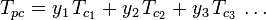
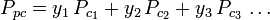
$T_{pc} = y_1,T_{c_1} + y_2,T_{c_2} + y_3,T_{c_3},ots$ $P_{pc} = y_1,P_{c_1} + y_2,P_{c_2} + y_3,P_{c_3},punten$

waar:
Tpc	= de pseudokritische temperatuur van het gasmengsel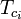
$T_{c_i}$	= de kritische temperatuur van een component van het gasmengsel
Ppc	= de pseudokritische druk van het gasmengsel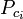
$P_{c_i}$	= de kritische temperatuur van een component van het gas
yi	= de mol- (of volumefractie) van een component van het gas

De pseudoreduced temperatuur, Tpr, en de pseudoreduceerde druk, Ppr, te gebruiken met de gegeneraliseerde samendrukbaarheidsfactor-grafieken voor zuivere gassen zijn dan:

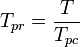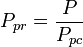
$T_{pr} = \frac{T}{T_{pc}}$ en $P_{pr} = \frac{P}{P_{pc}}$

Een samendrukbaarheidsfactorgrafiek voor aardgas (dat een mengsel is van koolwaterstof en andere gassen) met gebruikmaking van pseudoreduceerde temperaturen en drukken is beschikbaar op het Internet.

De van der Waals-vergelijking

De van der Waals-vergelijking werd in 1873 ontwikkeld en kan worden uitgedrukt als:

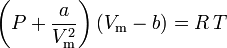
$-links(P + \frac{a}{V_mathrm{m}^2}rechts)\links(V_mathrm{m} - brechts) = R,T$

waarin:

a een maat is voor de aantrekkingskracht tussen de gasmoleculen b het door de gasmoleculen ingenomen volume weergeeft, waardoor het beschikbare open volume afneemt

De van der Waals vergelijking kan worden herschikt als:

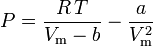
$P = \frac{R,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

en de samendrukbaarheidsfactor kan worden geschreven als:

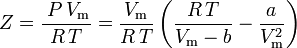
$Z = \frac{;P,V_mathrm{m}}{R,T} = \frac{V_mathrm{m}}{R,T} links(\frac{R,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2} rechts)$

en we hebben nu een vergelijking om Z te bepalen met behulp van de van der Waals parameters a en b:

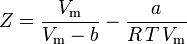
$Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R,T,V_\mathrm{m}}$

Hoewel a en b “de Van der Waals constanten” worden genoemd, zijn het geen echte constanten omdat ze van gas tot gas verschillen; ze zijn echter onafhankelijk van P, V en T. Met andere woorden, zij zijn constant voor het gas in kwestie. Gegeven de kritische temperatuur en druk voor een bepaald gas, kunnen a en b voor dat specifieke gas uit deze vergelijkingen worden verkregen:

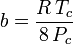
$a = \frac{27, R^2, T_c^2}{64, P_c}$ en $b = \frac{R\, T_c}{8, P_c}$

Bij voorbeeld, de kritische druk van ethaan is 4.884 MPa en de kritische temperatuur is 305,43 K (32,3˚C). Uitgaande van de universele gasconstante R van 8,3145 Pa m3 K-1 mol-1 geven bovenstaande vergelijkingen a = 0,557 m6 Pa mol-2 en b = 6,500×10-5 m3 mol-1.

Tabellen van de waarden van a en b voor diverse gassen zijn beschikbaar in deze referenties en in vele andere bronnen in de technische literatuur.

Gewijzigde versies van de van der Waals vergelijking

Het bepalen van samendrukbaarheidsfactoren met behulp van de van der Waals toestandsvergelijking is een verbetering ten opzichte van het gebruik van de gegeneraliseerde samendrukbaarheidstabellen. Er zijn echter aangepaste versies van de van der Waals toestandsvergelijking die nog meer verbetering geven. Wellicht de meest gebruikte toestandsvergelijkingen door ingenieurs die werkzaam zijn in de aardolieraffinage, petrochemische produktie, aardgasverwerking, cryogene distillatie en aanverwante industrieën zijn: de Redlich-Kwong vergelijking ontwikkeld in 1949, de Soave-Redlich-Kwong vergelijking ontwikkeld in 1972 en de Peng-Robinson vergelijking ontwikkeld in 1976. Deze drie vergelijkingen zijn in wezen gewijzigde versies van de van der Waals-vergelijking. De vergelijkende vergelijkingen zijn:

Redlich-Kwong

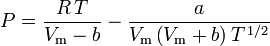
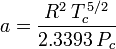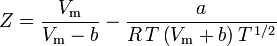
$P = \frac{R,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m} links(V_\mathrm {m} + b} rechts)T^{\,1/2}}$ $a = \frac{R^2, T_c^{\,5/2}}{2.3393, P_c}$ en $b = \frac{R\, T_c}{11.5420, P_c}$ $Z = \frac{V_mathrm{m}}{V_mathrm{m} - b} - \frac{a}{R\, T}links(V_mathrm {m} + b}rechts)T^{\,1/2}}$

Soave-Redlich-Kwong

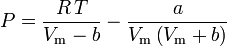
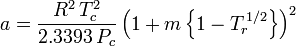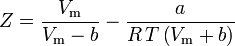
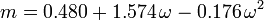
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}(V_\mathrm {m} + b}rechts)}$ $a = \frac{R^2,T_c^2}{2.3393,P_c}, \Big(1 + m, \Big{1 - T_r^{,1/2} \Big)^2$ en $b = \frac{R\, T_c}{11.5420, P_c}$ $Z = \frac{V_mathrm{m}}{V_mathrm{m} - b} - \frac{a}{R\, T}left(V_mathrm {m} + b}right)}$ $m = 0.480 + 1,574, γomega - 0,176, γomega^2$

De acentrieke factor, ω, die als parameter in de Soave-Redlich-Kwong en de Peng-Robinson vergelijkingen wordt gebruikt, werd voor het eerst geïntroduceerd door Pitzer et al in 1955. Hij kan worden uitgedrukt als:

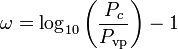
$omega = \log_{10} \links(\frac{P_c}{P_mathrm{vp}}rechts) - 1$

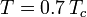waar Pvp de verzadigde dampspanning van het gas is bij een temperatuur van $T = 0,7, T_c$ .

Peng-Robinson

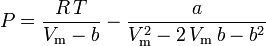
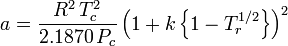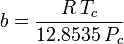
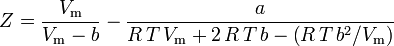
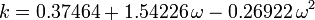
$P = \frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2 - 2,V_mathrm{m}, b - b^2}$ $a = \frac{R^2,T_c^2}{2.1870,P_c}, \Big(1 + k, \Big{1 - T_r^{1/2} \Big)^2$ en $b = \frac{R\, T_c}{12,8535, P_c}$ $Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m} + 2,R,T,b - links(R,T,b^2/V_\mathrm{m})}$ $k = 0,37464 + 1,54226, \omega - 0,26922, \omega^2$

Toestandsvergelijking van de virialen

De meest fundamentele toestandsvergelijking, in die zin dat zij de meest solide theoretische basis heeft, is de virialen toestandsvergelijking:

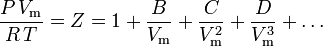
$V\,V\m}}{R\,T} = Z = 1 + \frac{B}{V\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots$

Het werd voor het eerst op empirische basis voorgesteld door Thiesen in 1885 en verder ontwikkeld in 1901 door Kamerlingh-Onnes. Een statistisch-mechanische uitdrukking voor B werd voor het eerst afgeleid door Ornstein in zijn proefschrift. De vergelijking werd vervolgens opnieuw ontwikkeld door H.D. Ursell in 1927 op een theoretische basis afgeleid van een statistisch-mechanische (cluster) analyse van intermoleculaire krachten.

De parameters B, C en D worden respectievelijk de tweede, derde en vierde viriale coëfficiënten genoemd. De coëfficiënten zijn geen constanten, want zij variëren van gas tot gas en ook met de temperatuur van het beschouwde gas. Zij worden soms geschreven als B(T), C(T) en D(T) om aan te geven dat het functies van de temperatuur zijn. De numerieke waarde van de coëfficiënten moet experimenteel worden bepaald.

De tweede viriaalcoëfficiënt levert het grootste deel van de correctie voor het niet-ideale gedrag van een gas. Om die reden wordt de viriale vergelijking soms afgekapt na de term die de tweede coëfficiënt bevat. Wanneer echter de derde coëfficiënt beschikbaar is, wordt de vergelijking meestal afgekapt na de term die de derde coëfficiënt bevat. De vierde coëfficiënt is zelden beschikbaar.

Een uitgebreide compilatie van viriale coëfficiënten voor zuivere gassen en gasmengsels werd opgesteld uit de viriale coëfficiëntendatabase van het Thermodynamics Research Center, voorheen van de Texas A&M University, College Station, Texas en nu gevestigd in het National Institute of Standards and Technology (NIST), Boulder, Colorado. De laatste versie van die compilatie werd gepubliceerd in 2003. NIST biedt ook een softwareprogramma aan, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), dat tweede en derde viriaalcoëfficiënten bevat, evenals een groot aantal andere thermodynamische eigenschappen.

Andere toestandsvergelijkingen

Er zijn een aantal andere toestandsvergelijkingen voor het voorspellen van het gedrag van echte gassen. De bekendste zijn wellicht de Beattie-Bridgeman-vergelijking, ontwikkeld in 1929, en de Benedict-Rubin-Webb-vergelijking, ontwikkeld in 1940. In het algemeen zijn zij complexer dan de vergelijkingen die hierboven zijn besproken.

Notatie voor de gasconstante

De gasconstante die in dit artikel wordt gebruikt is de universele gasconstante, R, die voor elk gas geldt. Er is ook een specifieke gasconstante, die kan worden aangeduid als Rs, en gedefinieerd is als Rs = R / M waarbij M het molecuulgewicht is.

Helaas gebruiken veel auteurs in de technische literatuur soms R als de specifieke gasconstante zonder deze als zodanig aan te duiden of te vermelden dat het de specifieke gasconstante is. Dit kan en zal tot verwarring leiden.

1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. and Simon, John D. (1999). Moleculaire Thermodynamica. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal and Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2e editie. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, Seventh Edition. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (India). ISBN 81-7371-048-1.
5.0 5.1 Gaswetten (Lezing door professor M.J. Mombourquette aan de Queens University, Canada)
Hong Wei Xiang (2005). Het principe van de overeenstemmende staten en de praktijk: Thermodynamische, Transport en Oppervlakte Eigenschappen van Vloeistoffen. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). “Modified Law of Corresponding States”. Industriële & Technische scheikunde 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Toestandsvergelijkingen (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Toestandsvergelijkingen (Lezingenmateriaal gebruikt door Professor Sanford Klein aan de Universiteit van Wisconsin-Madison, V.S.)
Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3e editie. McGraw-Hill. ISBN 0-07-042366-0. (Zie figuur G-1 op blz. G.145)
Kai-Fui Vincent Wong (2000). Thermodynamica voor ingenieurs, 1e Editie. CRC Press. ISBN 0-8493-0232-3. (Zie figuur A-2, blz. 278}
Nelson-Obert gegeneraliseerde samendrukbaarheidsgrafieken (Grafieken beschikbaar op internet, van de website van San Diego State University, V.S.)
W.B.Kay (1936). “Gassen en dampen bij hoge temperatuur en druk – Dichtheid van koolwaterstof”. Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
Yunus A. Çengal and Michael A. Bowes (2005). Thermodynamica: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Lezingenmateriaal van professor R.M. Price aan de Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Noorse Universiteit voor Wetenschap en Technologie)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56e editie. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Hoofdstuk 3: Toestandsvergelijkingen (pagina’s 6-8 van 65 pdf pagina’s) (Deel van PhD thesis door Ji Lin Wang, 2002, Swinbourne University of Technology, Australië)
20.0 20.1 20.2 Jean Vidal (2003). Thermodynamica: Applications in Chemical Engineering and the Petroleum Industry. Editions Technip. ISBN 2-7108-0800-5.
Zakia Nasri en Housam Binous (2007). “Toepassingen van de Soave-Redlich-Kwong toestandsvergelijking met behulp van Mathematica”. Tijdschrift voor Chemische Technologie van Japan 40 (6): 534-538. Hier vandaan gehaald.
K.S. Pitzer et al (1955). “The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning en Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Acentric Factor Definition (Physical Property Sources Index, PPSI, van het Zwitserse Federale Instituut voor Technologie Zürich)
Max F. Thiesen (1885). “Onderzoeken van de toestandsvergelijking”. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). “Expression of the Equation of State of Gases and Liquids by Means of Series”. Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken, Leiden
H. D. Ursell (1927). “The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
J.D. Dymond and R.C. Wilhoit (Auteurs), K.N. Marsch and M. Fenkel (Redacteuren) (2003). Viriale coëfficiënten van zuivere gassen en mengsels, 1e editie. Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie and O.C. Bridgeman (1929). “A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb and L.C. Rubin (1940). “An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.

Bepaalde inhoud van deze pagina is mogelijk eerder op Citizendium verschenen.

Opgehaald van “http://knowino.org/wiki/Compressibility_factor_(gases)”

Categorie: Natuurkunde