Automat komórkowy to zbiór „kolorowych” komórek na siatce o określonym kształcie, która ewoluuje przez pewną liczbę dyskretnych kroków czasowych zgodnie z zestawem reguł opartych na stanach sąsiednich komórek. Reguły te są następnie stosowane iteracyjnie przez dowolną liczbę kroków czasowych. von Neumann był jedną z pierwszych osób, które rozważały taki model i włączył model komórkowy do swojego „uniwersalnego konstruktora”. Automaty komórkowe były badane na początku lat 50-tych jako możliwy model dla systemów biologicznych (Wolfram 2002, str. 48). Kompleksowe badania nad automatami komórkowymi zostały przeprowadzone przez S. Wolframa począwszy od lat 80-tych, a fundamentalne badania Wolframa w tej dziedzinie zakończyły się publikacją jego książki A New Kind of Science (Wolfram 2002), w której Wolfram przedstawia gigantyczny zbiór wyników dotyczących automatów, wśród których znajduje się wiele przełomowych nowych odkryć.
Odcinek 2 sezonu „Bettor or Worse” (2006) telewizyjnego dramatu kryminalnego NUMB3RS wspomina o jednowymiarowych automatach komórkowych.
Automaty komórkowe występują w różnych kształtach i odmianach. Jedną z najbardziej fundamentalnych właściwości automatu komórkowego jest rodzaj siatki, na której jest on obliczany. Najprostszą taką „siatką” jest jednowymiarowa linia. W dwóch wymiarach mogą być rozważane siatki kwadratowe, trójkątne i sześciokątne. Automaty komórkowe mogą być również konstruowane na siatkach kartezjańskich w dowolnej liczbie wymiarów, z 
wymiarową siatką liczb całkowitych 
jako najbardziej powszechnym wyborem. Automaty komórkowe na 
wymiarowej siatce liczb całkowitych są zaimplementowane w języku Wolframa jako CellularAutomaton.
Liczba kolorów (lub odrębnych stanów) 
, które automat komórkowy może przyjąć, musi być również określona. Liczba ta jest zwykle liczbą całkowitą, przy czym 
(binarny) jest najprostszym wyborem. Dla automatu binarnego, kolor 0 jest powszechnie nazywany „białym”, a kolor 1 jest powszechnie nazywany „czarnym”. Jednak automaty komórkowe posiadające ciągły zakres możliwych wartości również mogą być brane pod uwagę.
Oprócz siatki, na której żyje automat komórkowy i kolorów, jakie mogą przybierać jego komórki, musi być również określone sąsiedztwo, w którym komórki wpływają na siebie nawzajem. Najprostszy wybór to „najbliżsi sąsiedzi”, w którym tylko komórki bezpośrednio sąsiadujące z daną komórką mogą być dotknięte w każdym kroku czasowym. Dwa typowe sąsiedztwa w przypadku dwuwymiarowego automatu komórkowego na kwadratowej siatce to tzw. sąsiedztwo Moore’a (sąsiedztwo kwadratowe) i sąsiedztwo von Neumanna (sąsiedztwo w kształcie rombu).
Najprostszym typem automatu komórkowego jest binarny, najbliższy sąsiad, jednowymiarowy automat. Takie automaty zostały nazwane „elementarnymi automatami komórkowymi” przez S. Wolframa, który obszernie badał ich niesamowite własności (Wolfram 1983; 2002, s. 57). Istnieje 256 takich automatów, z których każdy może być indeksowany przez unikalną liczbę binarną, której dziesiętna reprezentacja jest znana jako „reguła” dla danego automatu. Ilustracja reguły 30 jest pokazana powyżej wraz z ewolucją, którą wytwarza po 15 krokach, zaczynając od pojedynczej czarnej komórki.
Nieco bardziej skomplikowaną klasą automatów komórkowych są najbliżej sąsiadujące, 
kolorowe, jednowymiarowe totalistyczne automaty komórkowe. W takich automatach to średnie z sąsiednich komórek określają ewolucję, a najprostsze nietrywialne przykłady mają 
kolory. Dla tych automatów zbiór reguł opisujących zachowanie można zakodować jako 
cyfrową 
liczbę znaną jako „kod”. Reguły i 300 kroków trójskładnikowego (
) automatu kodowego 912 są zilustrowane powyżej.
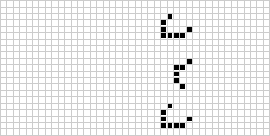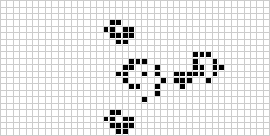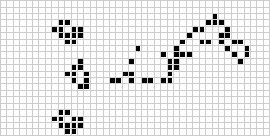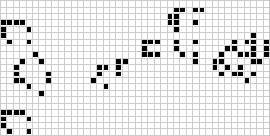
W dwóch wymiarach najbardziej znanym automatem komórkowym jest gra życia Conwaya, odkryta przez J. H. Conwaya w 1970 roku i spopularyzowana w felietonach Martina Gardnera w Scientific American. Gra o życie jest binarnym (
) totalistycznym automatem komórkowym z sąsiedztwem Moore’a o zakresie 
. Choć początkowo obliczanie kolejnych generacji gry życia było wykonywane ręcznie, wkrótce nadeszła rewolucja komputerowa, która pozwoliła na badanie i propagację bardziej rozbudowanych wzorców. Animacja konstrukcji game of life znanej jako puffer train jest zilustrowana powyżej.
WireWorld jest innym wspólnym dwuwymiarowym cellularautomaton.
Teoria automatów komórkowych jest niezmiernie bogata, z prostymi regułami i strukturami będącymi w stanie wyprodukować wielką różnorodność nieoczekiwanych zachowań. Na przykład, istnieją uniwersalne automaty komórkowe, które są w stanie symulować zachowanie każdego innego automatu komórkowego lub maszyny Turinga. Zostało to nawet udowodnione przez Gacsa (2001), że istnieją odporne na błędy uniwersalne automaty komórkowe, których zdolność do symulowania innych automatów komórkowych nie jest utrudniona przez losowe perturbacje, pod warunkiem, że takie perturbacje są wystarczająco rzadkie.
.