Biografia

Brahmagupta (598-668 CE)
Wielki 7-wieczny indyjski matematyk i astronom Brahmagupta napisał kilka ważnych prac zarówno na temat matematyki, jak i astronomii. Pochodził ze stanu Radżastan w północno-zachodnich Indiach (jest często określany jako Bhillamalacarya, nauczyciel z Bhillamala), a później został szefem obserwatorium astronomicznego w Ujjain w środkowych Indiach. Większość jego prac są skomponowane w eliptycznym wersie, powszechną praktyką w indyjskiej matematyki w tym czasie, a zatem mają coś z poetyckim pierścieniem do nich.
Wydaje się prawdopodobne, że prace Brahmagupty, zwłaszcza jego najsłynniejszy tekst, „Brahmasphutasiddhanta”, zostały przywiezione przez kalifa Abbasydów Al-Mansura w VIII wieku do jego nowo założonego centrum nauki w Bagdadzie na brzegach Tygrysu, zapewniając ważny związek między indyjską matematyką i astronomią a rodzącym się rozkwitem nauki i matematyki w świecie islamskim.
W jego pracy na arytmetyce, Brahmagupta wyjaśniał jak znaleźć sześcian i sześcian-korzeń liczby całkowitej i dał zasady ułatwiające obliczanie kwadratów i pierwiastków kwadratowych. Podał też zasady postępowania z pięcioma rodzajami kombinacji ułamków. Sumę kwadratów pierwszych n liczb naturalnych podał jako n(n + 1)(2n + 1)⁄ 6, a sumę sześcianów pierwszych n liczb naturalnych jako (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Treat Zero as a Number

Reguły Brahmagupty dotyczące radzenia sobie z zerem i liczbami ujemnymi
Geniusz Brahmagupty, though, came in his treatment of the concept of (then relatively new) the number zero. Choć często przypisuje się ją matematykowi Bhaskara I z VII wieku, jego „Brahmasphutasiddhanta” jest prawdopodobnie najwcześniejszym znanym tekstem traktującym zero jako liczbę samą w sobie, a nie po prostu jako cyfrę zastępczą, jak czynili to Babilończycy, lub jako symbol braku ilości, jak czynili to Grecy i Rzymianie.
Brahmagupta ustanowił podstawowe matematyczne zasady postępowania z zerem (1 + 0 = 1; 1 – 0 = 1; i 1 x 0 = 0), chociaż jego rozumienie dzielenia przez zero było niekompletne (myślał, że 1 ÷ 0 = 0). Prawie 500 lat później, w XII wieku, inny indyjski matematyk, Bhaskara II, wykazał, że odpowiedzią powinna być nieskończoność, a nie zero (na tej podstawie, że 1 można podzielić na nieskończoną liczbę kawałków o rozmiarze zero), odpowiedź, którą przez wieki uważano za poprawną. Jednak ta logika nie wyjaśnia, dlaczego 2 ÷ 0, 7 ÷ 0, itd. również powinno być zero – współczesny pogląd jest taki, że liczba podzielona przez zero jest w rzeczywistości „nieokreślona” (tj. nie ma sensu).
Pogląd Brahmagupty na liczby jako abstrakcyjne byty, a nie tylko do liczenia i mierzenia, pozwolił mu dokonać jeszcze jednego ogromnego skoku pojęciowego, który miał głębokie konsekwencje dla przyszłej matematyki. Wcześniej, na przykład, suma 3 – 4 była uważana albo za bezsensowną, albo, w najlepszym wypadku, za zero. Brahmagupta zdał sobie jednak sprawę, że może istnieć coś takiego jak liczba ujemna, którą nazwał „długiem” w odróżnieniu od „własności”. On expounded na zasady postępowania z liczbami ujemnymi (np. ujemny razy ujemny jest dodatni, ujemny razy dodatni jest ujemny, itp.).
Furthermore, on wskazał, równania kwadratowe (typu x2 + 2 = 11, na przykład) może w teorii mieć dwa możliwe rozwiązania, z których jeden może być ujemny, ponieważ 32 = 9 i -32 = 9. Oprócz swojej pracy nad rozwiązaniami ogólnych równań liniowych i równań kwadratowych, Brahmagupta poszedł jeszcze dalej, rozważając układy równań równoczesnych (zestaw równań zawierający wiele zmiennych) i rozwiązując równania kwadratowe z dwiema niewiadomymi, coś, co nie było nawet rozważane na Zachodzie aż do tysiąca lat później, kiedy Fermat rozważał podobne problemy w 1657 roku.
Twierdzenie Brahmagupty o cyklicznych czworokątach
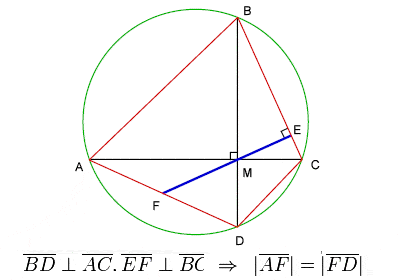
Twierdzenie Brahmagupty o cyklicznych czworokątach
Brahmagupta próbował nawet zapisać te dość abstrakcyjne pojęcia, używając inicjałów nazw kolorów do reprezentowania niewiadomych w swoich równaniach, co było jedną z najwcześniejszych oznak tego, co obecnie znamy jako algebrę.
Brahmagupta poświęcił znaczną część swojej pracy geometrii i trygonometrii. Ustanowił √10 (3.162277) jako dobre praktyczne przybliżenie dla π (3.141593) i podał wzór, obecnie znany jako Wzór Brahmagupty, na pole powierzchni cyklicznego czworokąta, jak również słynne twierdzenie o przekątnych cyklicznego czworokąta, zwykle określane jako Twierdzenie Brahmagupty.
| << Powrót do matematyki indyjskiej | Dalej do Madhavy >> |
.