Nieokreślony układ liniowy
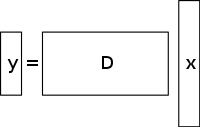
Nieokreślony układ równań liniowych ma więcej niewiadomych niż równań i na ogół ma nieskończoną liczbę rozwiązań. Poniższy rysunek przedstawia taki układ równań y = D x { {displaystyle \mathbf {} =D\mathbf {x} }

gdzie chcemy znaleźć rozwiązanie dla x { {displaystyle \mathbf {x} }

.
Aby wybrać rozwiązanie takiego układu, należy nałożyć dodatkowe ograniczenia lub warunki (takie jak gładkość), stosownie do potrzeb. W kompresji czujników dodaje się ograniczenie rozproszenia, dopuszczając tylko rozwiązania, które mają małą liczbę niezerowych współczynników. Nie wszystkie niezdeterminowane układy równań liniowych mają rozwiązanie rzadkie. Jednakże, jeśli istnieje unikalne, rzadkie rozwiązanie układu nieokreślonego, wtedy ramy kompresji pozwalają na odzyskanie tego rozwiązania.
Metoda rozwiązania / rekonstrukcji

Compressed sensing wykorzystuje redundancję w wielu interesujących sygnałach – nie są one czystym szumem. W szczególności wiele sygnałów jest rzadkich, to znaczy zawierają wiele współczynników bliskich lub równych zeru, gdy są reprezentowane w jakiejś dziedzinie. Jest to ten sam wgląd używany w wielu formach stratnej kompresji.
Compressed sensing zazwyczaj zaczyna się od podjęcia ważonej kombinacji liniowej próbek zwanych również pomiarami kompresyjnymi w podstawie innej niż podstawa, w której sygnał jest znany jako nieliczny. Wyniki odkryte przez Emmanuel Candès, Justin Romberg, Terence Tao i David Donoho, pokazały, że liczba tych pomiarów kompresyjnych może być niewielka i nadal zawierać prawie wszystkie użyteczne informacje. Dlatego zadanie konwersji obrazu z powrotem do zamierzonej dziedziny polega na rozwiązaniu równania macierzy niedookreślonej, ponieważ liczba wykonanych pomiarów kompresyjnych jest mniejsza niż liczba pikseli w pełnym obrazie. Jednak dodanie ograniczenia, że sygnał początkowy jest rzadki, umożliwia rozwiązanie tego nieustalonego układu równań liniowych.
Najmniejszym kwadratowym rozwiązaniem takich problemów jest minimalizacja równania L 2 {{2}}}

normy – czyli zminimalizowanie ilości energii w układzie. Zwykle jest to proste matematycznie (wymaga jedynie mnożenia macierzy przez pseudo-inwersję podstawy, w której próbkowane są dane). Jednak prowadzi to do słabych wyników dla wielu praktycznych zastosowań, dla których nieznane współczynniki mają niezerową energię.
Aby wymusić warunek rzadkości podczas rozwiązywania nieokreślonego układu równań liniowych, można zminimalizować liczbę niezerowych składowych rozwiązania. Funkcja zliczająca liczbę niezerowych składowych wektora została nazwana funkcją L 0 {{0}}

„normą” przez Davida Donoho.
Candès et al. udowodnili, że dla wielu problemów jest prawdopodobne, że L 1 {{displaystyle L^{1}}

norma jest równoważna normie L 0 {displaystyle L^{0}}

normą, w sensie technicznym: Ten wynik równoważności pozwala rozwiązać normę L 1 {displaystyle L^{1}}

, co jest łatwiejsze niż problem L 0 {displaystyle L^{0}}

problem. Znalezienie kandydata o najmniejszym L 1 {displaystyle L^{1}}

normie można stosunkowo łatwo wyrazić jako program liniowy, dla którego istnieją już efektywne metody rozwiązania. W przypadku, gdy pomiary mogą zawierać skończoną ilość szumu, denoising bazowy jest preferowany w stosunku do programowania liniowego, ponieważ zachowuje on nieciągłość w obliczu szumu i może być rozwiązany szybciej niż dokładny program liniowy.
Total variation based CS reconstruction
Motywacja i zastosowania
Rola regularyzacji telewizyjnej
Zmienność całkowitą można postrzegać jako nieujemną funkcję rzeczywisto-wartościową zdefiniowaną na przestrzeni funkcji rzeczywisto-wartościowych (dla przypadku funkcji jednej zmiennej) lub na przestrzeni funkcji całkowalnych (dla przypadku funkcji kilku zmiennych). Dla sygnałów, w szczególności, całkowita zmienność odnosi się do całki z bezwzględnego gradientu sygnału. W rekonstrukcji sygnałów i obrazów stosuje się ją jako regularyzację całkowitej wariacji, gdzie podstawową zasadą jest to, że sygnały z nadmierną ilością szczegółów mają wysoką całkowitą wariację i że usunięcie tych szczegółów, przy zachowaniu ważnych informacji, takich jak krawędzie, zmniejszyłoby całkowitą wariację sygnału i sprawiłoby, że obiekt sygnału byłby bliższy oryginalnemu sygnałowi w problemie.
Dla celów rekonstrukcji sygnałów i obrazów, l 1 {\i0}

stosuje się modele minimalizacyjne. Inne podejścia obejmują również najmniejsze kwadraty, jak to zostało omówione wcześniej w tym artykule. Metody te są bardzo powolne i zwracają niezbyt doskonałą rekonstrukcję sygnału. Obecne modele regularizacji CS próbują rozwiązać ten problem poprzez włączenie priorytetów rozproszenia oryginalnego obrazu, z których jednym jest całkowita zmienność (TV). Konwencjonalne podejścia do TV są zaprojektowane tak, aby dawać stałe rozwiązania. Niektóre z nich obejmują (jak omówiono wcześniej) – ograniczoną l1-minimalizację, która wykorzystuje schemat iteracyjny. Metoda ta, choć szybka, prowadzi następnie do nadmiernego wygładzania krawędzi, co skutkuje rozmyciem krawędzi obrazu. W celu zmniejszenia wpływu dużych wartości gradientu w obrazie zastosowano metody TV z iteracyjnym ponownym ważeniem. Zostało to wykorzystane w rekonstrukcji tomografii komputerowej (CT) jako metoda znana jako zachowująca krawędzie (ang. edge-preserving total variation). Jednakże, ponieważ wielkości gradientu są używane do estymacji względnych wag kar między wiernością danych a warunkami regularyzacji, metoda ta nie jest odporna na szumy i artefakty oraz wystarczająco dokładna dla rekonstrukcji obrazu/sygnału CS, a zatem nie zachowuje mniejszych struktur.
Ostatni postęp w tym problemie polega na użyciu iteracyjnie kierunkowego TV refinement dla rekonstrukcji CS. Metoda ta składałaby się z dwóch etapów: w pierwszym etapie szacowane i udoskonalane byłoby początkowe pole orientacji – które jest definiowane jako hałaśliwa, punktowa estymacja początkowa, poprzez detekcję krawędzi, danego obrazu. W drugim etapie, model rekonstrukcji CS jest prezentowany poprzez wykorzystanie kierunkowego TV regularizera. Więcej szczegółów na temat tych podejść opartych na TV – iteracyjnie ważona minimalizacja l1, TV zachowująca krawędzie i model iteracyjny wykorzystujący kierunkowe pole orientacji i TV – jest podanych poniżej.
Istniejące podejścia
Iteracyjnie ważona minimalizacja l 1 {{1}}


minimalizacja

W modelach rekonstrukcji CS wykorzystujących constrained l 1 {{1}}

minimalizacji, większe współczynniki są silnie karane w metodzie l 1 {displaystyle l_{1}}

norm. Zaproponowano ważone sformułowanie normy l 1 {displaystyle l_{1}}

minimalizacji, zaprojektowaną w celu bardziej demokratycznego karania niezerowych współczynników. Do konstrukcji odpowiednich wag wykorzystywany jest algorytm iteracyjny. Każda iteracja wymaga rozwiązania jednego l 1 {{1}}

problemu minimalizacji poprzez znalezienie lokalnego minimum wklęsłej funkcji kary, która bardziej przypomina funkcję l 0 {{displaystyle l_{0}}

norm. Dodatkowy parametr, zwykle w celu uniknięcia ostrych przejść w krzywej funkcji kary, jest wprowadzany do równania iteracyjnego, aby zapewnić stabilność i aby zerowe oszacowanie w jednej iteracji nie musiało prowadzić do zerowego oszacowania w następnej iteracji. Metoda polega zasadniczo na wykorzystaniu bieżącego rozwiązania do obliczania wag, które mają być wykorzystane w następnej iteracji.
Wady i zalety
Wczesne iteracje mogą znaleźć niedokładne estymaty próbkowania, jednak ta metoda obniży próbkowanie na późniejszym etapie, aby nadać większą wagę mniejszym niezerowym estymatom sygnału. Jedną z wad jest potrzeba zdefiniowania ważnego punktu początkowego, ponieważ globalne minimum może nie zostać uzyskane za każdym razem z powodu wklęsłości funkcji. Inną wadą jest to, że metoda ta ma tendencję do równomiernego karania gradientu obrazu niezależnie od struktury obrazu. Powoduje to nadmierne wygładzanie krawędzi, szczególnie tych w regionach o niskim kontraście, co w konsekwencji prowadzi do utraty informacji o niskim kontraście. Zalety tej metody to: zmniejszenie częstotliwości próbkowania dla sygnałów rzadkich; rekonstrukcja obrazu przy jednoczesnym zachowaniu odporności na usuwanie szumów i innych artefaktów; oraz użycie bardzo małej liczby iteracji. To może również pomóc w odzyskiwaniu obrazów z gradientami sparse.
Na rysunku pokazanym poniżej, P1 odnosi się do pierwszego kroku iteracyjnego procesu rekonstrukcji, macierzy projekcji P geometrii wiązki wachlarzowej, która jest ograniczona przez termin wierności danych. Może ona zawierać szumy i artefakty, ponieważ nie jest wykonywana regularizacja. Minimalizacja P1 jest rozwiązywana za pomocą metody najmniejszych kwadratów z gradientem sprzężonym. P2 odnosi się do drugiego kroku iteracyjnego procesu rekonstrukcji, w którym wykorzystuje się zachowujący krawędzie termin regularyzacji całkowitej zmienności w celu usunięcia szumów i artefaktów, a tym samym poprawy jakości zrekonstruowanego obrazu/sygnału. Minimalizacja P2 jest wykonywana za pomocą prostej metody zstępowania gradientu. Zbieżność jest określana poprzez testowanie, po każdej iteracji, pozytywności obrazu, poprzez sprawdzenie, czy f k – 1 = 0 {{displaystyle f^{k-1}=0}}

dla przypadku, gdy f k – 1 < 0 {displaystyle f^{k-1}<0}

(Zauważmy, że f {displaystyle f}

odnosi się do różnych współczynników tłumienia liniowego promieniowania rentgenowskiego w różnych wokselach obrazu pacjenta).
Edge-preserving total variation (TV) based compressed sensing

Jest to iteracyjny algorytm rekonstrukcji CT z zachowaniem krawędzi (edge-preserving TV regularization) do rekonstrukcji obrazów CT z wysoce niedopróbkowanych danych uzyskanych w CT o niskiej dawce przez niskie poziomy prądu (miliampery). W celu zmniejszenia dawki obrazowania, jednym ze stosowanych podejść jest zmniejszenie liczby projekcji rentgenowskich pozyskiwanych przez detektory skanera. Jednak ta niewystarczająca liczba danych projekcyjnych, które są wykorzystywane do rekonstrukcji obrazu TK, może powodować artefakty smużenia. Co więcej, użycie tych niewystarczających projekcji w standardowych algorytmach TV powoduje, że problem staje się niedookreślony, co prowadzi do nieskończenie wielu możliwych rozwiązań. W tej metodzie, do oryginalnej normy TV przypisana jest dodatkowa funkcja ważona karą. Pozwala to na łatwiejsze wykrywanie ostrych nieciągłości intensywności w obrazach, a tym samym dostosowanie wagi do przechowywania odzyskanej informacji o krawędziach w procesie rekonstrukcji sygnału/obrazu. Parametr σ {sigma }
kontroluje ilość wygładzania zastosowanego do pikseli na krawędziach w celu odróżnienia ich od pikseli nie będących krawędziami. Wartość σ {{displaystyle \sigma }
. W ten sposób wariancja całkowita zachowująca krawędzie staje się mniejsza, a to przyspiesza implementację. Stosowany jest dwuetapowy proces iteracji znany jako algorytm podziału przód-tył. Problem optymalizacyjny jest dzielony na dwa podproblemy, które są następnie rozwiązywane odpowiednio metodą najmniejszych kwadratów ze sprzężonym gradientem i prostą metodą zstępowania gradientowego. Metoda jest zatrzymywana po osiągnięciu pożądanej zbieżności lub po osiągnięciu maksymalnej liczby iteracji.
Wady i zalety
Niektóre z wad tej metody to brak mniejszych struktur w zrekonstruowanym obrazie i degradacja rozdzielczości obrazu. Ten algorytm TV z zachowaniem krawędzi wymaga jednak mniejszej liczby iteracji niż konwencjonalny algorytm TV. Analizując poziome i pionowe profile intensywności zrekonstruowanych obrazów można zauważyć, że występują ostre skoki w punktach krawędziowych i pomijalne, niewielkie fluktuacje w punktach nie krawędziowych. Dzięki temu metoda ta prowadzi do niskiego błędu względnego i wyższej korelacji w porównaniu do metody TV. Skutecznie tłumi i usuwa również wszelkie formy szumów i artefaktów obrazu, takich jak smużenie.
Model iteracyjny wykorzystujący kierunkowe pole orientacji i kierunkową zmienność całkowitą
Aby zapobiec nadmiernemu wygładzaniu krawędzi i szczegółów tekstury oraz uzyskać zrekonstruowany obraz CS, który jest dokładny i odporny na szumy i artefakty, stosuje się tę metodę. Po pierwsze, wstępna estymacja zaszumionego pola orientacji punkt-wise obrazu I {displaystyle I}

, d ^ {{displaystyle {{d}}}

, otrzymuje się. To zaszumione pole orientacji jest zdefiniowane tak, aby można je było dopracować na późniejszym etapie w celu zmniejszenia wpływu szumu na estymację pola orientacji. Następnie wprowadzana jest zgrubna estymacja pola orientacji w oparciu o tensor struktury, który jest sformułowany jako: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) { { {{}}}}}(∇ I_{}} })=G_{\rho }*(\nabla I_{\sigma })={{begin{pmatrix}J_{11}&J_{12}&J_{22}}}end{pmatrix}}.

. Tutaj, J ρ {{displaystyle J_{rho }}

odnosi się do tensora struktury związanego z punktem piksela obrazu (i,j) o odchyleniu standardowym ρ {\displaystyle J_{\rho }

. G {{displaystyle G}

odnosi się do jądra gaussowskiego ( 0 , ρ 2 ) {displaystyle (0,^{2})}

z odchyleniem standardowym ρ { {displaystyle ^{2})}

. σ {displaystyle \sigma }
odnosi się do ręcznie zdefiniowanego parametru dla obrazu I { {displaystyle I}

, poniżej którego wykrywanie krawędzi jest niewrażliwe na szum. ∇ I σ {displaystyle \nabla I_{sigma }}

odnosi się do gradientu obrazu I { {displaystyle I}

oraz ( ∇ I σ ⊗ ∇ I σ ) {displaystyle (∇ I_{sigma }})

odnosi się do iloczynu tensorowego otrzymanego przez zastosowanie tego gradientu.
Uzyskany tensor struktury jest konwertowany z gaussowskim jądrem G {{displaystyle G}}

w celu poprawy dokładności estymaty orientacji z σ {displaystyle \sigma }
ustawiono na wysokie wartości w celu uwzględnienia nieznanego poziomu szumu. Dla każdego piksela (i,j) w obrazie, tensor struktury J jest symetryczną i dodatnią macierzą pół-definitywną. Konwolucja wszystkich pikseli w obrazie za pomocą G {{displaystyle G}}

, daje ortonormalne wektory własne ω i υ macierzy J {displaystyle J}

macierzy. ω wskazuje w kierunku orientacji dominującej o największym kontraście, a υ wskazuje w kierunku orientacji struktury o najmniejszym kontraście. Pole orientacji zgrubna estymacja początkowa d ^ {{displaystyle {{d}}}

definiuje się jako d ^ {displaystyle {{d}}}

= υ. To oszacowanie jest dokładne przy silnych krawędziach. Jednak przy słabych krawędziach lub w regionach z szumem jego wiarygodność spada.
To pole orientacji jest wprowadzane do kierunkowego modelu optymalizacji całkowitej zmienności dla rekonstrukcji CS poprzez równanie:

. X {{displaystyle \mathrm {X} }

jest macierzą pomiarową CS. Metoda ta przechodzi kilka iteracji ostatecznie prowadząc do zbieżności. d ^ {displaystyle {{d}}}

jest przybliżoną estymacją pola orientacji zrekonstruowanego obrazu X k – 1 {displaystyle X^{k-1}}

z poprzedniej iteracji (w celu sprawdzenia zbieżności i późniejszej wydajności optycznej używana jest poprzednia iteracja). Dla dwóch pól wektorowych reprezentowanych przez X {{displaystyle {X} }

i d {displaystyle d}

, X ∙ d {displaystyle \mathrm {X} „>
i d {displaystyle d}

odnosi się do mnożenia odpowiednich elementów wektora poziomego i pionowego X {displaystyle \mathrm {X} }

i d {{displaystyle d}

, po czym następuje ich kolejne dodawanie. Równania te są sprowadzane do serii wypukłych problemów minimalizacyjnych, które są następnie rozwiązywane za pomocą kombinacji metod podziału zmiennych i rozszerzonego Lagrangiana (oparty na FFT szybki solver z rozwiązaniem w formie zamkniętej). Metoda ta (Augmented Lagrangian) jest uważana za równoważną dzielonej iteracji Bregmana, która zapewnia zbieżność tej metody. Pole orientacji, d jest zdefiniowane jako równe ( d h , d v ) {d_{h},d_{v})}

, gdzie d h , d v {displaystyle d_{h},d_{v}}

definiują poziome i pionowe oszacowania d {displaystyle d}

.

Metoda Augmented Lagrangian dla pola orientacji,

, polega na inicjalizacji d h , d v , H , V {{displaystyle d_{h},d_{v},H,V}}.

, a następnie znalezienie przybliżonego minimalizatora L 1 {displaystyle L_{1}}

względem tych zmiennych. Następnie mnożniki Lagrangiana są aktualizowane, a proces iteracyjny jest zatrzymywany po osiągnięciu zbieżności. W przypadku iteracyjnego kierunkowego modelu rafinacji wariancji całkowitej, metoda rozszerzonego Lagrangiana polega na inicjalizacji X , P , Q , λ P , λ Q {{displaystyle \mathrm {X} ,P,Q,\lambda _{P},\lambda _{Q}}

.
Tutaj H , V , P , Q {{displaystyle H,V,P,Q}}

są nowo wprowadzonymi zmiennymi, gdzie H {{displaystyle H}

= ∇ d h {{displaystyle \nabla d_{h}}

, V {{displaystyle V}

= ∇ d v {displaystyle \nabla d_{v}}

, P {{displaystyle P}

= ∇ X { {displaystyle \nabla {X} }

, a Q {{displaystyle Q}

= P ∙ d {{displaystyle P}

. λ H , λ V , λ P , λ Q {displaystyle ∙lambda _{H},∙lambda _{V},∙lambda _{P},∙lambda _{Q}}

są mnożnikami Lagrangiana dla H , V , P , Q {displaystyle H,V,P,Q}}.

. Dla każdej iteracji, przybliżony minimalizator L 2 {displaystyle L_{2}}

w odniesieniu do zmiennych ( X , P , Q {{displaystyle {X} ,P,Q}}

). I tak jak w modelu rafinacji pola, mnożniki lagrangianu są uaktualniane, a proces iteracyjny jest zatrzymywany po osiągnięciu zbieżności.
W przypadku modelu udoskonalania pola orientacji, mnożniki Lagrangiana są uaktualniane w procesie iteracyjnym w następujący sposób:
( λ H )k = ( λ H )k – 1 + γ H ( H k – ∇ ( d h )k ) { {przykłady (^{H})^{k}=(^{H})^{k-1}+gamma _{H}(H^{k}-nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) { {displaystyle (\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-\nabla (d_{v})^{k})}

Dla iteracyjnego kierunkowego modelu rafinacji wariacji całkowitej, mnożniki Lagrangiana są aktualizowane w następujący sposób:
( λ P )k = ( λ P )k – 1 + γ P ( P k – ∇ ( X )k ) { {przykład (ˆlambda _{P})^{k}=(ˆlambda _{P})^{k-1}+ ˆgamma _{P}(P^{k}- ˆnabla (ˆmathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) { {displaystyle (^lambda _{Q}})^{k}=(^lambda _{Q})^{k-1}+gamma _{Q}(Q^{k}-P^{k}}}}bullet d)}

Tutaj, γ H , γ V , γ P , γ Q {displaystyle \gamma _{H},\gamma _{V},\gamma _{P},\gamma _{Q}}

są stałymi dodatnimi.
Wady i zalety
Based on peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) metrics and known ground-truth images for testing performance, iterative directional total variation has a better reconstructed performance than the non-iterative methods in preserving edge and texture areas. Model rafinacji pola orientacji odgrywa główną rolę w tej poprawie wydajności, ponieważ zwiększa liczbę bezkierunkowych pikseli w płaskim obszarze, jednocześnie zwiększając spójność pola orientacji w regionach z krawędziami.