Maszyna Boltzmanna

Są to stochastyczne procesy uczenia się posiadające strukturę rekurencyjną i stanowią podstawę wczesnych technik optymalizacji stosowanych w ANN. Maszyna Boltzmanna została wynaleziona przez Geoffrey’a Hintona i Terry’ego Sejnowskiego w 1985 roku. Więcej jasności można zaobserwować w słowach Hintona na temat Maszyny Boltzmanna.

„Zaskakującą cechą tej sieci jest to, że wykorzystuje ona tylko lokalnie dostępną informację. Zmiana wagi zależy tylko od zachowania dwóch jednostek, które łączy, mimo że zmiana ta optymalizuje globalną miarę” – Ackley, Hinton 1985.

Kilka ważnych punktów o Maszynie Boltzmanna –

• Używają struktury rekurencyjnej.

• Składają się z neuronów stochastycznych, które mają jeden z dwóch możliwych stanów, albo 1 albo 0.

• Część neuronów w tej sieci jest adaptacyjna (stan wolny), a część jest zaciśnięta (stan zamrożony).

• Jeśli zastosujemy symulowane wyżarzanie na dyskretnej sieci Hopfielda, to stanie się ona maszyną Boltzmanna.

Cel Maszyny Boltzmanna

Głównym celem Maszyny Boltzmanna jest optymalizacja rozwiązania jakiegoś problemu. Praca maszyny Boltzmanna polega na optymalizacji wag i ilości związanych z tym konkretnym problemem.

Architektura

Następujący diagram pokazuje architekturę maszyny Boltzmanna. Z diagramu jasno wynika, że jest to dwuwymiarowa tablica jednostek. Tutaj wagi połączeń między jednostkami wynoszą -p gdzie p > 0. Wagi połączeń własnych są dane przez b gdzie b > 0.

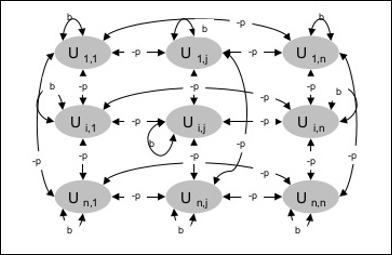
Algorytm treningowy

Jak wiemy, maszyny Boltzmanna mają stałe wagi, stąd nie będzie algorytmu treningowego, gdyż nie musimy aktualizować wag w sieci. Jednakże, aby przetestować sieć musimy ustawić wagi, jak również znaleźć funkcję konsensusu (CF).

Maszyna Boltzmanna posiada zbiór jednostek Ui i Uj oraz posiada na nich dwukierunkowe połączenia.

• Rozważamy stałą wagę powiedzmy wij.

• wij ≠ 0 jeśli Ui i Uj są połączone.

• Istnieje również symetria w ważonych połączeniach wzajemnych, tzn.tj. wij = wji.

• wii również istnieje, czyli istniałoby samopołączenie między jednostkami.

• Dla dowolnej jednostki Ui, jej stan ui byłby albo 1 albo 0. \w_{ij}u_{i}u_{j}$$

  Teraz, gdy stan zmienia się z 1 na 0 lub z 0 na 1, to zmiana konsensusu może być dana następującą zależnością –

  $Delta CF:=(1:- 2u_{i})(w_{ij})(w_{ij})$$

  Tutaj ui jest bieżącym stanem Ui.

  Zmiana współczynnika (1 – 2ui) jest dana następującą zależnością –

  $$(1u_{i})\(1u_{i})\(2u_{i})\(1u_{i})\(1u_{i})\i), & U_{i}$(1 – 2u_{i})\i), & U_{i}$(1 – 2u_{i})\i} jest stanem początkowym{cases}+1, & U_{i}off{cases}-1, & U_{i}:is:currently:on{cases}$$

  Generalnie jednostka Ui nie zmienia swojego stanu, ale gdyby tak się stało, to informacja rezydowałaby lokalnie w jednostce. Wraz z tą zmianą, nastąpiłby również wzrost konsensusu sieci.

  Prawdopodobieństwo zaakceptowania przez sieć zmiany stanu jednostki jest dane następującą zależnością –

  $$AF(i,T)\=frac{1}{1:+:exp}$$

  T jest tutaj parametrem kontrolnym. Będzie się zmniejszać, gdy CF osiągnie maksymalną wartość.

  Algorytm testujący

  Krok 1 – Zainicjuj następujące elementy, aby rozpocząć trening –

  • Wagi reprezentujące ograniczenia problemu
  • Parametr kontrolny T

  Krok 2 – Kontynuuj kroki 3-8, gdy warunek zatrzymania nie jest prawdziwy.

  Krok 3 – Wykonaj kroki 4-7.

  Krok 4 – Załóż, że jeden ze stanów zmienił wagę i wybierz liczby całkowite I, J jako wartości losowe pomiędzy 1 a n.

  Krok 5 – Oblicz zmianę konsensusu w następujący sposób –

  $Delta CF:=:(1:-:2u_{i})(w_{ij}:+:∗ suma limitów_{jakość} u_{i} w_{ij})$$

  Krok 6 – Oblicz prawdopodobieństwo, że ta sieć zaakceptuje zmianę stanu

  $AF(i,T)∗:=frac{1}{1}$

  Krok 7 – Zaakceptuj lub odrzuć tę zmianę w następujący sposób –

  Przypadek I – jeśli R < AF, zaakceptuj zmianę.

  Przypadek II – jeżeli R ≥ AF, odrzucić zmianę.

  Tutaj R jest liczbą losową z przedziału od 0 do 1.

  Krok 8 – Zmniejsz parametr sterujący (temperaturę) w następujący sposób –

  T(nowa) = 0.95T(old)

  Krok 9 – Przetestować warunki zatrzymania, które mogą być następujące –

  • Temperatura osiąga określoną wartość
  • Nie ma zmiany stanu przez określoną liczbę iteracji
  Przypisy

  .