Macierz konfuzji to tabela, która jest często używana do opisania wydajności modelu klasyfikacyjnego (lub „klasyfikatora”) na zestawie danych testowych, dla których znane są prawdziwe wartości. Sama macierz dezorientacji jest stosunkowo prosta do zrozumienia, ale związana z nią terminologia może być myląca.
Chciałem stworzyć „szybki przewodnik” po terminologii macierzy dezorientacji, ponieważ nie mogłem znaleźć istniejącego zasobu, który spełniałby moje wymagania: zwarta prezentacja, użycie liczb zamiast arbitralnych zmiennych i wyjaśnienie zarówno w postaci wzorów, jak i zdań.
Zacznijmy od przykładowej macierzy konfuzji dla klasyfikatora binarnego (choć można ją łatwo rozszerzyć na przypadek więcej niż dwóch klas):
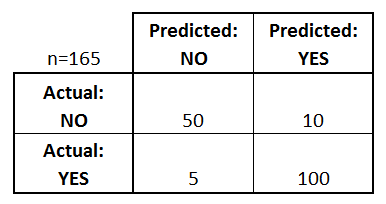
Czego możemy się dowiedzieć z tej macierzy?
- Istnieją dwie możliwe przewidywane klasy: „tak” i „nie”. Jeśli na przykład przewidywalibyśmy obecność choroby, „tak” oznaczałoby, że mają chorobę, a „nie” oznaczałoby, że nie mają choroby.
- Klasyfikator wykonał łącznie 165 przewidywań (np, 165 pacjentów było testowanych na obecność tej choroby).
- Wśród tych 165 przypadków klasyfikator przewidział „tak” 110 razy, a „nie” 55 razy.
- W rzeczywistości 105 pacjentów w próbie ma chorobę, a 60 pacjentów nie ma.
Zdefiniujmy teraz najbardziej podstawowe terminy, które są liczbami całkowitymi (nie wskaźnikami):
- wyniki prawdziwie pozytywne (TP): Są to przypadki, w których przewidzieliśmy, że tak (mają chorobę), a oni rzeczywiście mają chorobę.
- prawdziwe negatywy (TN): Przewidzieliśmy, że nie, a oni nie mają choroby.
- fałszywie dodatnie (FP): Przewidzieliśmy tak, ale oni faktycznie nie mają choroby. (Znany również jako „błąd typu I.”)
- fałszywe negatywy (FN): Przewidzieliśmy, że nie, ale oni rzeczywiście mają chorobę. (Znany również jako „błąd typu II.”)
Dodałem te terminy do macierzy konfuzji, a także dodałem sumy wierszy i kolumn:
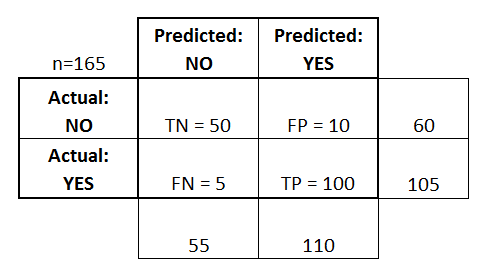
To jest lista wskaźników, które są często obliczane z macierzy konfuzji dla klasyfikatora binarnego:
- Dokładność: Overall, how often is the classifier correct?
- (TP+TN)/total = (100+50)/165 = 0.91
- Misclassification Rate: Ogólnie, jak często się myli?
- (FP+FN)/ogółem = (10+5)/165 = 0.09
- równowartość 1 minus Accuracy
- znany również jako „Error Rate”
- True Positive Rate: Kiedy jest to rzeczywiście tak, jak często przewiduje tak?
- TP / rzeczywiste tak = 100/105 = 0,95
- znany również jako „Sensitivity” lub „Recall”
- False Positive Rate: Kiedy jest to faktycznie nie, jak często przewiduje tak?
- FP / rzeczywiste nie = 10/60 = 0,17
- True Negative Rate: Kiedy jest to faktycznie nie, jak często przewiduje nie?
- TN/actual nie = 50/60 = 0,83
- równowartość 1 minus False Positive Rate
- znany również jako „Specificity”
- Precision: Kiedy przewiduje tak, jak często jest to poprawne?
- TP/predicted yes = 100/110 = 0.91
- Prevalence: Jak często warunek tak faktycznie występuje w naszej próbce?
- actual yes/total = 105/165 = 0.64
Warto też wspomnieć o kilku innych terminach:
- Null Error Rate: To jest jak często byś się mylił, gdybyś zawsze przewidywał klasę większości. (W naszym przykładzie stopa błędu zerowego wynosiłaby 60/165=0,36, ponieważ gdybyś zawsze przewidywał tak, myliłbyś się tylko w 60 przypadkach „nie”). To może być użyteczna metryka bazowa do porównania z klasyfikatorem. Jednakże, najlepszy klasyfikator dla danej aplikacji będzie miał czasami wyższy poziom błędu niż zerowy poziom błędu, jak pokazuje Paradoks Dokładności.
- Cohen’s Kappa: Jest to zasadniczo miara tego, jak dobrze klasyfikator wykonał w porównaniu do tego, jak dobrze wykonałby po prostu przez przypadek. Innymi słowy, model będzie miał wysoki wynik Kappa, jeśli istnieje duża różnica między dokładnością a zerowym poziomem błędu. (Więcej szczegółów o Cohen’s Kappa.)
- Wynik F: Jest to średnia ważona współczynnika prawdziwych pozytywów (recall) i precyzji (precision). (Więcej szczegółów na temat F Score.)
- Krzywa ROC: Jest to powszechnie używany wykres, który podsumowuje wydajność klasyfikatora na wszystkich możliwych progach. Jest on generowany przez wykreślenie współczynnika True Positive Rate (oś y) względem False Positive Rate (oś x) w miarę zmiany progu przypisywania obserwacji do danej klasy. (Więcej szczegółów na temat krzywych ROC.)
I wreszcie, dla tych z was ze świata statystyki bayesowskiej, oto szybkie podsumowanie tych terminów z Applied Predictive Modeling:
W odniesieniu do statystyki bayesowskiej, czułość i specyficzność są prawdopodobieństwami warunkowymi, częstość występowania jest prior, a pozytywne/negatywne przewidywane wartości są prawdopodobieństwami posterior.
Chcesz dowiedzieć się więcej?
W moim nowym 35-minutowym filmie wideo, Making sense of the confusion matrix, wyjaśniam te koncepcje bardziej dogłębnie i obejmuję bardziej zaawansowane tematy:
- Jak obliczać precyzję i recall dla problemów wieloklasowych
- Jak analizować 10-klasową macierz konfuzji
- Jak wybrać właściwą metrykę oceny dla swojego problemu
- Dlaczego dokładność jest często mylącą metryką
Daj mi znać, jeśli masz jakieś pytania!