Cel nauczania
1. Konwertowanie z jednej jednostki na inną jednostkę tego samego typu.
W rozdziale 2.2 „Wyrażanie jednostek” pokazaliśmy kilka przykładów, jak zastąpić jednostki początkowe innymi jednostkami tego samego typu, aby uzyskać wartość liczbową, która jest łatwiejsza do zrozumienia. W tym rozdziale sformalizujemy ten proces.
Rozważmy prosty przykład: ile stóp jest w 4 jardach? Większość ludzi niemal automatycznie odpowie, że w 4 jardach jest 12 stóp. W jaki sposób dokonaliście tego ustalenia? Cóż, jeśli na 1 jard przypadają 3 stopy, a jardów jest 4, to na 4 jardach jest 4 × 3 = 12 stóp.
Jest to oczywiście poprawne, ale nieformalne. Sformalizujmy to w sposób, który może być stosowany bardziej ogólnie. Wiemy, że 1 jard (yd) równa się 3 stopy (ft):
1 yd = 3 ft
W matematyce to wyrażenie nazywa się równością. Zasady algebry mówią, że możesz zmienić (tzn. pomnożyć, podzielić, dodać lub odjąć) równość (tak długo, jak nie dzielisz przez zero), a nowe wyrażenie nadal będzie równością. Na przykład, jeśli podzielimy obie strony przez 2, otrzymamy
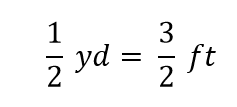
Widzimy, że pół jarda równa się 3/2, czyli półtora stopy – coś, co również wiemy, że jest prawdą, więc powyższe równanie nadal jest równością. Wracając do oryginalnej równości, załóżmy, że podzielimy obie strony równania przez 1 jard (liczbę i jednostkę):
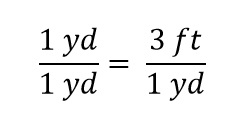
Wyrażenie nadal jest równością, zgodnie z zasadami algebry. Lewy ułamek równa się 1. Ma tę samą ilość w liczniku i mianowniku, więc musi być równy 1. Wielkości w liczniku i mianowniku anulują się, zarówno liczba, jak i jednostka:
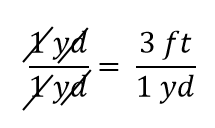
Gdy wszystko anuluje się w ułamku, ułamek redukuje się do 1:
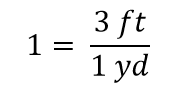
Mamy wyrażenie, 3 ft1 yd, które jest równe 1. Jest to dziwny sposób zapisu 1, ale ma sens: 3 ft równa się 1 yd, więc wielkości w liczniku i mianowniku są tymi samymi wielkościami, tylko wyrażonymi w różnych jednostkach. Wyrażenie 3 ft1 yd nazywamy współczynnikiem konwersji i używamy go do formalnej zamiany jednostki danej wielkości na inną jednostkę. (Proces konwersji jednostek w taki formalny sposób jest czasami nazywany analizą wymiarową lub metodą oznaczania czynnika.)
Aby zobaczyć, jak to się dzieje, zacznijmy od oryginalnej wielkości:
4 yd
Teraz pomnóżmy tę wielkość przez 1. Kiedy mnożymy cokolwiek przez 1, nie zmieniamy wartości wielkości. Zamiast mnożyć tylko przez 1, zapiszmy 1 jako 3 ft1 yd:
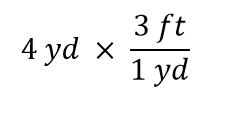
Wyraz 4 yd można traktować jako 4 yd/1; to znaczy, można go traktować jako ułamek z 1 w mianowniku. Zasadniczo mnożymy ułamki. Jeśli ta sama rzecz pojawia się w liczniku i mianowniku ułamka, to się one anulują. W tym przypadku to, co się anuluje, to jednostka jard:
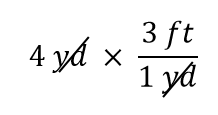
To wszystko, co możemy anulować. Teraz pomnóż i podziel wszystkie liczby, aby otrzymać ostateczną odpowiedź: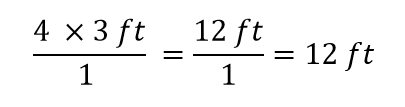
Ponownie, otrzymujemy odpowiedź 12 ft, tak jak w oryginale. Ale w tym przypadku użyliśmy bardziej formalnej procedury, która ma zastosowanie do różnych problemów.
Ile milimetrów mieści się w 14,66 m? Aby odpowiedzieć na to pytanie, musimy skonstruować współczynnik konwersji między milimetrami i metrami i zastosować go poprawnie do oryginalnej wielkości. Zaczynamy od definicji milimetra, która brzmi
1 mm = 1/1,000 m
1/1,000 oznacza przedrostek milli-. Większość ludzi czuje się bardziej komfortowo pracując bez ułamków, więc przepiszemy to równanie przenosząc 1,000 do licznika drugiej strony równania:
1,000 mm = 1 m
Teraz konstruujemy współczynnik konwersji dzieląc jedną wielkość na obie strony. Ale teraz pojawia się pytanie: przez którą wielkość dzielimy? Okazuje się, że mamy dwa wyjścia, a te dwa wyjścia dadzą nam różne współczynniki konwersji, z których oba są równe 1:
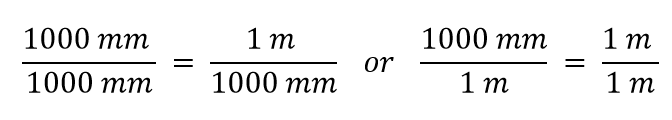
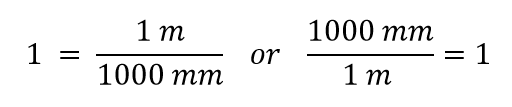
Którego współczynnika konwersji użyjemy? Odpowiedź jest oparta na tym, jakiej jednostki chcemy się pozbyć w naszej początkowej ilości. Oryginalną jednostką naszej ilości są metry, które chcemy przekonwertować na milimetry. Ponieważ zakłada się, że oryginalna jednostka jest w liczniku, aby się jej pozbyć, chcemy, aby jednostka metra była w mianowniku; wtedy się one znoszą. Dlatego użyjemy drugiego współczynnika konwersji. Odwołując jednostki i wykonując działania matematyczne, otrzymujemy
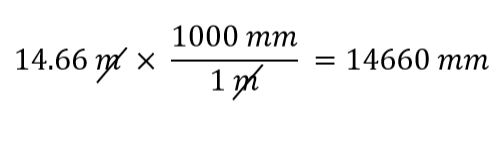
Zauważ, jak m się odwołuje, pozostawiając mm, które jest jednostką zainteresowania.
Umiejętność konstruowania i stosowania właściwych współczynników konwersji jest bardzo potężną techniką matematyczną w chemii. Musisz opanować tę technikę, jeśli chcesz odnieść sukces w tym i przyszłych kursach.
Przykład 7
- Przekształć 35,9 kL na litry.
- Przekształć 555 nm na metry.
Rozwiązanie
-
Użyjemy faktu, że 1 kL = 1000 L. Z dwóch współczynników konwersji, które można zdefiniować, ten, który będzie działał to 1000 L/1 kL. Stosując ten przelicznik, otrzymamy
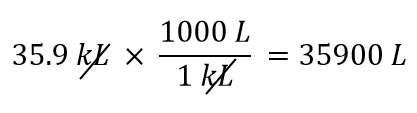
-
Wykorzystamy fakt, że 1 nm = 1/1 000 000 000 m, co zapiszemy jako 1 000 000 000 nm = 1 m lub 109 nm = 1 m. Z dwóch możliwych przeliczników właściwy ma w mianowniku jednostkę nm: 1 m/109 nm. Stosując ten współczynnik konwersji, otrzymujemy
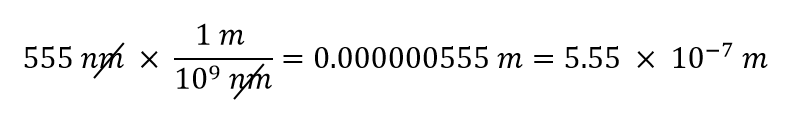
W ostatnim kroku wyraziliśmy odpowiedź w notacji naukowej.
Test Yourself
- Przelicz 67.08 μL na litry.
- Przekształć 56,8 m na kilometry.
Odpowiedzi
- 6,708 × 10-5 L
- 5,68 × 10-2 km
A co jeśli mamy jednostkę pochodną, która jest iloczynem więcej niż jednej jednostki, np. m2? Załóżmy, że chcemy przeliczyć metry kwadratowe na centymetry kwadratowe? Kluczem jest zapamiętanie, że m2 oznacza m × m, co oznacza, że mamy dwie jednostki metrowe w naszej jednostce pochodnej. Oznacza to, że musimy uwzględnić dwa współczynniki konwersji, po jednym dla każdej jednostki. Na przykład, aby przekonwertować 17,6 m2 na centymetry kwadratowe, wykonujemy konwersję w następujący sposób:
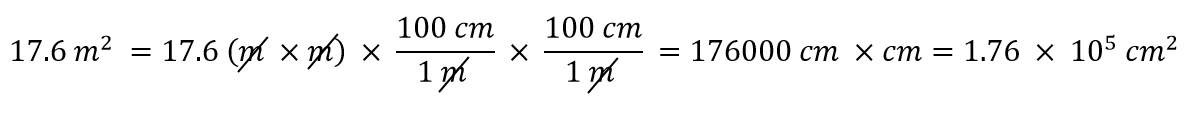
Przykład 8
Ile centymetrów sześciennych mieści się w 0.883 m3?
Rozwiązanie
Przy wykładniku 3 mamy trzy jednostki długości, więc przez rozszerzenie musimy użyć trzech przeliczników między metrami i centymetrami. Mamy więc
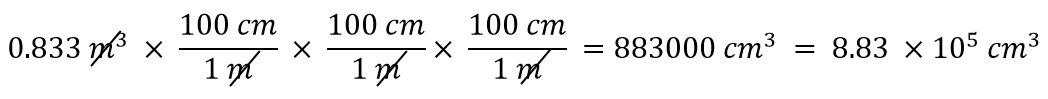
Powinieneś wykazać, że trzy jednostki metrów rzeczywiście się znoszą.
Test Yourself
Ile milimetrów sześciennych jest obecnych w 0,0923 m3?
Odpowiedź
9,23 × 107 mm3
Załóżmy, że jednostka, którą chcemy przeliczyć jest w mianowniku jednostki pochodnej; co wtedy? Wtedy, we współczynniku konwersji, jednostka, którą chcesz usunąć, musi być w liczniku. Spowoduje to anulowanie oryginalnej jednostki w mianowniku i wprowadzenie nowej jednostki w mianowniku. Poniższy przykład ilustruje tę sytuację.
Przykład 9
Przekształć 88,4 m/min na metry/sekundę.
Rozwiązanie
Chcemy zmienić jednostkę w mianowniku z minut na sekundy. Ponieważ w 1 minucie jest 60 sekund (60 s = 1 min), konstruujemy przelicznik tak, aby jednostka, którą chcemy usunąć, czyli minuty, znalazła się w liczniku: 1 min/60 s. Zastosuj i wykonaj matematykę:
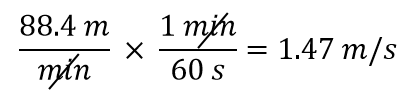
Zauważ, jak 88,4 automatycznie trafia do licznika. To dlatego, że każda liczba może być uważana za znajdującą się w liczniku ułamka podzielonego przez 1.
Test Yourself
Przelicz 0.203 m/min na metry/sekundę.
Odpowiedź
0.00338 m/s lub 3,38 × 10-3 m/s
Figure 2.8 How Fast Is Fast?

Źródło: „Grapevine snail „by Jürgen Schoneris licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
.