
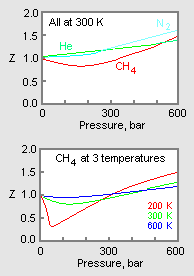
Rysunek 1: Przykładowe wykresy współczynników ściśliwości gazów
Współczynnik ściśliwości (Z) jest użyteczną właściwością termodynamiczną służącą do modyfikacji prawa gazów idealnych w celu uwzględnienia zachowania gazów rzeczywistych. Jest to miara tego, jak bardzo właściwości termodynamiczne gazu rzeczywistego odbiegają od tych oczekiwanych od gazu idealnego. Można o nim myśleć jako o stosunku rzeczywistej objętości gazu rzeczywistego do objętości przewidywanej przez gaz idealny w tej samej temperaturze i ciśnieniu, co rzeczywista objętość.
Dla gazu idealnego, Z zawsze ma wartość 1. Dla gazów rzeczywistych, wartość może odbiegać dodatnio lub ujemnie, w zależności od wpływu sił międzycząsteczkowych gazu. Im bliżej punktu krytycznego lub punktu nasycenia znajduje się gaz rzeczywisty, tym większe są jego odchylenia od idealnego zachowania.
Górny wykres na rysunku 1 ilustruje, jak zmienia się współczynnik ściśliwości dla różnych gazów w tej samej temperaturze i pod tym samym ciśnieniem. Dolny wykres ilustruje, jak współczynnik ściśliwości gazu (na przykład metanu) przy danym ciśnieniu zmienia się w zależności od temperatury.
W niniejszym artykule omówiono tylko współczynnik ściśliwości gazów i nie zagłębiano się w ściśliwość cieczy lub mieszanin para-ciecz.
Spis treści
- 1 Wyznaczanie wartości współczynnika ściśliwości gazu
- 1.1 Uogólnione wykresy współczynnika ściśliwości dla czystych gazów
- 1.2 Uogólnione wykresy współczynnika ściśliwości dla mieszanin gazów
- 1.3 Równanie van der Waalsa
- 1.3.1 Zmodyfikowane wersje równania van der Waalsa
- 1.3.1.1 Redlich-Kwong
- 1.3.1.2 Soave-Redlich-Kwong
- 1.3.1.3 Peng-Robinson
- 1.3.1 Zmodyfikowane wersje równania van der Waalsa
- 1.4 Virial equation of state
- 1.5 Other equations of state
- 1.6 Notacja dla stałej gazowej
- 2 Referencje
Wyznaczanie wartości ściśliwości gazu
Prawo gazu idealnego definiuje się jako:
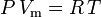
oraz prawo gazu idealnego skorygowane o nieidealność definiuje się jako:
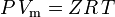
| gdzie: | |
| P | = ciśnienie |
|---|---|
| Vm | = objętość molowa gazu |
| Z | =. współczynnik ściśliwości |
| R | = uniwersalna stała gazowa |
| T | = temperatura |
a zatem:
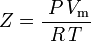
co jest najprostszym i najczęściej stosowanym równaniem stanu gazu rzeczywistego (EOS). Głównym ograniczeniem tego równania stanu jest to, że współczynnik ściśliwości gazu, Z, nie jest stały, lecz zmienia się w zależności od gazu, jak również od temperatury i ciśnienia rozważanego gazu. Musi on być wyznaczony doświadczalnie.
Gdy dostępne są dane doświadczalne dla określonych gazów, dane te mogą być wykorzystane do sporządzenia wykresów (takich jak na rysunku 1) zależności Z od ciśnienia w stałej temperaturze lub zależności Z od ciśnienia w różnych temperaturach dla tych określonych gazów. Takie wykresy są przydatne do łatwego uzyskiwania interpolowanych wartości Z pomiędzy wartościami wyznaczonymi doświadczalnie.
Współczynnik ściśliwości, jak wspomniano wcześniej, może być również wyrażony jako:
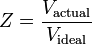
Istnieją trzy reżimy, które wpływają na współczynnik ściśliwości:
- wartość Z dąży do 1, gdy ciśnienie gazu zbliża się do 0, gdzie wszystkie gazy dążą do idealnego zachowania
- wartość Z jest mniejsza niż 1 przy pośrednich ciśnieniach, ponieważ międzycząsteczkowe siły przyciągania powodują, że rzeczywiste objętości są mniejsze niż idealne wartości
- wartość Z jest większa niż 1 i ostatecznie dąży do nieskończoności przy wysokich ciśnieniach, ponieważ siły odpychania międzycząsteczkowego powodują, że objętości rzeczywiste są większe od wartości idealnych
Uogólnione wykresy współczynnika ściśliwości dla czystych gazów
Wyjątkowa zależność pomiędzy współczynnikiem ściśliwości a temperaturą zredukowaną, Tr, i zredukowanym ciśnieniem Pr, została po raz pierwszy rozpoznana przez van der Waalsa w 1873 roku i jest znana jako dwuparametrowa zasada stanów odpowiadających. Zasada stanów odpowiadających wyraża uogólnienie, że właściwości gazu, które zależą od sił międzycząsteczkowych, są związane z właściwościami krytycznymi gazu w sposób uniwersalny. Stanowi to najważniejszą podstawę do opracowania korelacji właściwości molekularnych.
Jeśli chodzi o ściśliwość gazów, zasada stanów odpowiadających wskazuje, że każdy czysty gaz w tej samej obniżonej temperaturze, Tr, i obniżonym ciśnieniu, Pr, powinien mieć ten sam współczynnik ściśliwości.
Temperatura zredukowana i ciśnienie zredukowane są zdefiniowane jako:
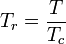 i
i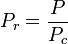
Tc i Pc są znane jako temperatura krytyczna i ciśnienie krytyczne gazu. Są one charakterystyczne dla każdego gazu, przy czym Tc jest temperaturą, powyżej której nie jest możliwe skroplenie danego gazu, a Pc jest minimalnym ciśnieniem wymaganym do skroplenia danego gazu w jego temperaturze krytycznej. Razem definiują one punkt krytyczny płynu, powyżej którego nie istnieją odrębne fazy ciekła i gazowa danego płynu.
Dane ciśnienie-wolumen-temperatura (PVT) dla rzeczywistych gazów różnią się w zależności od czystego gazu. Jednakże, gdy współczynniki ściśliwości różnych gazów jednoskładnikowych są wykreślane w zależności od ciśnienia wraz z izotermami temperaturowymi (jak pokazano dla metanu na dolnym wykresie na Rysunku 1), wiele wykresów wykazuje podobne kształty izoterm.
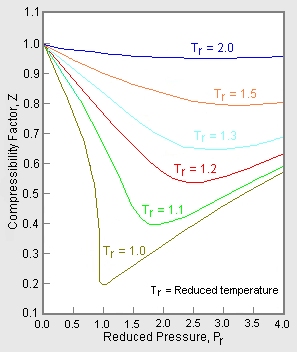
Rysunek 2: Przykład uogólnionego wykresu współczynnika ściśliwości
W celu uzyskania uogólnionego wykresu, który może być stosowany dla wielu różnych gazów, do normalizacji danych współczynnika ściśliwości stosuje się zredukowane ciśnienie i temperaturę, Pr i Tr. Rysunek 2 jest przykładem uogólnionego wykresu współczynnika ściśliwości uzyskanego z setek eksperymentalnych punktów danych P-V-T dla 10 czystych gazów, a mianowicie metanu, etanu, etylenu, propanu, n-butanu, i-pentanu, n-heksanu, azotu, dwutlenku węgla i pary wodnej.
Istnieją bardziej szczegółowe uogólnione wykresy współczynnika ściśliwości oparte na aż 25 lub więcej różnych czystych gazach, takie jak wykresy Nelsona-Oberta. Mówi się, że takie wykresy mają dokładność w granicach 1-2 procent dla wartości Z większych niż 0,6 i w granicach 4-6 procent dla wartości Z 0,3-0,6.
Uogólnione wykresy współczynnika ściśliwości mogą być obarczone znacznym błędem w przypadku gazów silnie polarnych, czyli gazów, dla których środki ładunku dodatniego i ujemnego nie pokrywają się. W takich przypadkach oszacowanie dla Z może być obarczone błędem nawet o 15-20 procent.
Gazy kwantowe wodór, hel i neon nie są zgodne z zachowaniem stanów odpowiadających i zredukowane ciśnienie i temperatura dla tych trzech gazów powinny być ponownie zdefiniowane w następujący sposób, aby poprawić dokładność przewidywania ich współczynników ściśliwości przy użyciu uogólnionych wykresów:
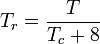 i
i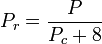
gdzie temperatury są w stopniach Kelvina, a ciśnienia w atmosferach.
Uogólnione wykresy współczynnika ściśliwości dla mieszanin gazowych
Uogólnione wykresy współczynnika ściśliwości dla czystych gazów (takie jak przykład na rysunku 2 lub wykresy Nelsona-Oberta mogą być również stosowane dla mieszanin gazowych poprzez użycie Reguły Kaya zaproponowanej przez W. B. Kaya w 1936 roku. Reguła ta przewiduje zachowanie P-V-T mieszaniny gazów poprzez określenie współczynnika ściśliwości dla mieszaniny gazów w obniżonej temperaturze i obniżonym ciśnieniu zdefiniowanych w kategoriach temperatury pseudokrytycznej, Tpc i ciśnienia pseudokrytycznego, Ppc, które są zdefiniowane jako:
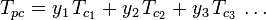
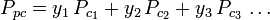
| gdzie: | |
| Tpc | = temperatura pseudokrytyczna mieszaniny gazów |
|---|---|
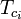 |
= temperatura krytyczna składnika mieszanki gazowej |
| Ppc | = ciśnienie pseudokrytyczne ciśnienie mieszaniny gazowej |
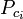 |
= temperatura krytyczna składnika gazu |
| yi | = ułamek molowy (lub objętościowy) składnika gazu |
Temperatura pseudoredukowana, Tpr, i pseudoredukowane ciśnienie, Ppr, do użycia z uogólnionymi wykresami współczynnika ściśliwości dla czystych gazów wynoszą:
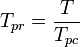 i
i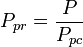
W Internecie dostępny jest wykres współczynnika ściśliwości dla gazu ziemnego (który jest mieszaniną węglowodorów i innych gazów) wykorzystujący pseudoredukowane temperatury i ciśnienia.
Równanie van der Waalsa
Równanie van der Waalsa zostało opracowane w 1873 r. i może być wyrażone jako:
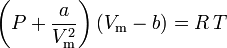
gdzie:
a jest miarą siły przyciągania między cząsteczkami gazu b uwzględnia objętość zajmowaną przez cząsteczki gazu, co zmniejsza dostępną objętość otwartą
Równanie van der Waalsa można przekształcić jako:
Z = ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗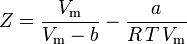
Aczkolwiek a i b są określane jako „stałe Van der Waalsa”, nie są one tak naprawdę stałymi, ponieważ różnią się w zależności od gazu; są jednak niezależne od P, V i T. Innymi słowy, są one stałe dla danego gazu. Biorąc pod uwagę temperaturę krytyczną i ciśnienie krytyczne dla danego gazu, a i b można uzyskać dla tego gazu z następujących równań:
 i
i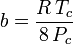
Na przykład ciśnienie krytyczne etanu wynosi 4.884 MPa, a temperatura krytyczna wynosi 305,43 K (32,3˚C). Stosując uniwersalną stałą gazową, R, wynoszącą 8,3145 Pa m3 K-1 mol-1, powyższe równania dają a = 0,557 m6 Pa mol-2 i b = 6,500×10-5 m3 mol-1.
Tablicowe wartości a i b dla różnych gazów są dostępne w tych referencjach, jak również w wielu innych źródłach w literaturze technicznej.
Zmodyfikowane wersje równania van der Waalsa
Określanie współczynników ściśliwości za pomocą równania stanu van der Waalsa jest ulepszeniem w stosunku do stosowania uogólnionych wykresów ściśliwości. Istnieją jednak zmodyfikowane wersje równania stanu van der Waalsa, które zapewniają jeszcze większą poprawę. Prawdopodobnie najczęściej używanymi równaniami stanu przez inżynierów pracujących przy rafinacji ropy naftowej, produkcji petrochemicznej, przetwarzaniu gazu ziemnego, destylacji kriogenicznej i w pokrewnych branżach są: równanie Redlicha-Kwonga opracowane w 1949 roku, równanie Soave’a-Redlicha-Kwonga opracowane w 1972 roku oraz równanie Peng-Robinsona opracowane w 1976 roku. Te trzy równania są w istocie zmodyfikowanymi wersjami równania van der Waalsa. Równaniami porównawczymi są:
Redlich-Kwong
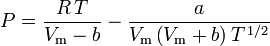
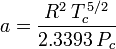 i
i
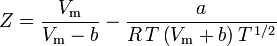
Soave-Redlich-Kwong
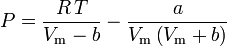
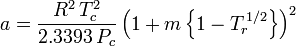 i
i
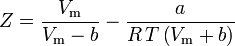
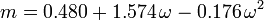
Współczynnik acentryczny, ω, używany jako parametr w równaniach Soave’a-Redlicha-Kwonga i Peng-Robinsona, został po raz pierwszy wprowadzony przez Pitzera et al w 1955 roku. Można go wyrazić jako:
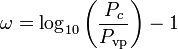
gdzie Pvp jest ciśnieniem pary nasyconej gazu w temperaturze 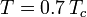 .
.
Peng-Robinson
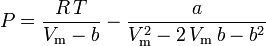
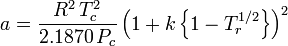 i
i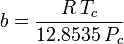
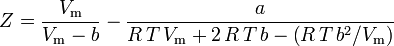
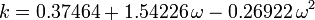
Wirialne równanie stanu
Najbardziej fundamentalnym równaniem stanu , w tym sensie, że ma najsolidniejsze podstawy teoretyczne, jest wirialne równanie stanu: + \frac{C}{V_ \mathrm{m}^2} + \frac{D}{V_mathrm{m}^3} + \frac{C}{V_mathrm{m}^2} + \dots
Po raz pierwszy został zaproponowany na podstawie empirycznej przez Thiesena w 1885 roku i dalej rozwinięty w 1901 roku przez Kamerlingh-Onnesa. Statystyczno-mechaniczne wyrażenie dla B zostało po raz pierwszy wyprowadzone przez Ornsteina w jego pracy doktorskiej. Równanie to zostało następnie ponownie opracowane przez H.D. Ursella w 1927 r. na podstawie teoretycznej wyprowadzonej ze statystyczno-mechanicznej (klastrowej) analizy sił międzycząsteczkowych.
Parametry B, C i D są nazywane odpowiednio drugim, trzecim i czwartym współczynnikiem wirialnym. Współczynniki te nie są stałe, ponieważ różnią się w zależności od gazu, jak również od temperatury rozważanego gazu. Czasami zapisuje się je jako B(T), C(T) i D(T), aby zaznaczyć, że są one funkcjami temperatury. Wartość liczbowa tych współczynników musi być określona doświadczalnie.
Drugi współczynnik wiriala zapewnia największą część poprawki na nieidealne zachowanie gazu. Dla ten powód, the virial równanie być czasem ucinać po the warunek zawierać the drugi współczynnik. Jednakże, gdy trzeci współczynnik jest dostępny, równanie jest zwykle skrócone po terminie zawierającym trzeci współczynnik. Czwarty współczynnik jest rzadko dostępny.
Duża kompilacja współczynników wirialnych dla czystych gazów i mieszanin gazów została przygotowana z bazy danych współczynników wirialnych w Centrum Badań Termodynamiki, dawniej w Texas A&M University, College Station, Texas, a obecnie znajdującej się w National Institute of Standards and Technology (NIST), Boulder, Colorado. Ostatnia wersja tej kompilacji została opublikowana w 2003 roku. NIST oferuje również do nabycia program komputerowy, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), który zawiera drugi i trzeci współczynnik viriala, jak również wiele innych właściwości termodynamicznych.
Inne równania stanu
Istnieje szereg innych równań stanu do przewidywania zachowania rzeczywistych gazów. Być może, najbardziej znane są równania Beattie-Bridgeman opracowane w 1929 roku i równanie Benedict-Rubin-Webb opracowane w 1940 roku. Ogólnie rzecz biorąc, są one bardziej złożone niż równania omówione powyżej.
Notacja dla stałej gazowej
Stała gazowa używana w tym artykule jest uniwersalną stałą gazową, R, która ma zastosowanie do każdego gazu. Istnieje również specyficzna stała gazowa, która może być oznaczana jako Rs, i jest zdefiniowana jako Rs = R / M, gdzie M jest masą cząsteczkową.
Niestety, wielu autorów w literaturze technicznej czasami używa R jako specyficznej stałej gazowej bez oznaczenia jej jako takiej lub stwierdzenia, że jest to specyficzna stała gazowa. To może i prowadzi do nieporozumień.
- 1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. i Simon, John D. (1999). Molecular Thermodynamics. University Science Books. ISBN 1-891389-05-X.
- 2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal and Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2nd Edition. McGraw-Hill Professional. ISBN 0-07-245426-1.
- 3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduction to Chemical Engineering Thermodynamics, Seventh Edition. McGraw Hill. ISBN 0-07-310445-0.
- 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemical Engineering Thermodynamics. Universities Press (India). ISBN 81-7371-048-1.
- 5.0 5.1 Prawa gazowe (Wykład profesora M.J. Mombourquette na Queens University, Kanada)
- Hong Wei Xiang (2005). The Corresponding States Principle and Its Practice: Thermodynamic, Transport and Surface Properties of Fluids. Elsevier. ISBN 0-444-52062-7.
- IUPAC Goldbook
- Gouq-Jen Su (1946). „Zmodyfikowane prawo odpowiadających sobie stanów”. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
- 9.0 9.1 Równania stanu (Profesor Lyes Kadem, Concordia University, Kanada)
- 10.0 10.1 Równania stanu (Materiały do wykładów wykorzystywane przez profesora Sanforda Kleina na Uniwersytecie Wisconsin-Madison, USA)
- Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3rd Edition. McGraw-Hill. ISBN 0-07-042366-0. (Patrz Rysunek G-1 na stronie G.145)
- Kai-Fui Vincent Wong (2000). Thermodynamics for Engineers, 1st Edition. CRC Press. ISBN 0-8493-0232-3. (Patrz Rysunek A-2, Strona 278}
- Nelson-Obert Generalized Compressibility Charts (Wykresy dostępne w Internecie, ze strony San Diego State University, U.S.)
- W.B.Kay (1936). „Gases and Vapors At High Temperature and Pressure – Density of Hydrocarbon” (Gazy i pary w wysokiej temperaturze i ciśnieniu – gęstość węglowodorów). Inżynieria Przemysłowa & Chemia 28:1014. ISSN 0096-4484.
- Yunus A. Çengal and Michael A. Bowes (2005). Termodynamika: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
- Real Gases (Materiały do wykładów wykorzystywane przez profesora R.M. Price na Christian Brothers University, U.S.A.)
- Properties of Natural Gases (Profesor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
- Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
- 19.0 19.1 19.2 Rozdział 3: Równania stanu (strony 6-8 z 65 stron pdf) (Część pracy doktorskiej przez Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
- 20.0 20.1 20.2 Jean Vidal (2003). Thermodynamics: Zastosowania w inżynierii chemicznej i przemyśle naftowym. Editions Technip. ISBN 2-7108-0800-5.
- Zakia Nasri i Housam Binous (2007). „Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Retrieved from here.
- K.S. Pitzer et al (1955). „The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
- Francis S. Manning and Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
- Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
- Max F. Thiesen (1885). „Investigations of the Equation of State”. Annalen der Physik und Chemie (24): 467-492.
- Heike Kamerlingh-Onnes (1901). „Expression of the Equation of State of Gases and Liquids by Means of Series”. Commun. Phys. Lab. Leiden (71).
- S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Zastosowanie statystycznej mechaniki Gibbsa na molekularno-teoretyczne problemy), Leiden
- H. D. Ursell (1927). „The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
- J.D. Dymond i R.C. Wilhoit (Autorzy), K.N. Marsch i M. Fenkel (Redaktorzy) (2003). Virial Coefficients of Pure gases and Mixtures, 1st Edition. Springer. ISBN 3-540-44340-1.
- NIST Standard Reference Database 23
- J.A. Beattie i O.C. Bridgeman (1929). „A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
- M. Benedict, G.B. Webb and L.C. Rubin (1940). „An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.
| |
Niektóre treści na tej stronie mogły się wcześniej pojawić na Citizendium. |
.