Współrzędne barycentryczne

przez
Geometria > GeometriaWspółrzędnych >
Geometria > Geometria Płaszczyznowa > Trójkąty > Własności trójkątów >

Współrzędne barycentryczne są trójkami liczb (t_1,t_2,t_3) odpowiadające masom umieszczonym w wierzchołkach trójkąta odniesienia DeltaA_1A_2A_3. Masy te wyznaczają następnie punkt P, który jest geometryczną centroidą trzech mas i jest identyfikowany ze współrzędnymi (t_1,t_2,t_3). Wierzchołki trójkąta są dane przez (1,0,0), (0,1,0), oraz (0,0,1). Współrzędne barycentryczne zostały odkryte przez Möbiusa w 1827 roku (Coxeter 1969, s. 217; Fauvel et al. 1993).

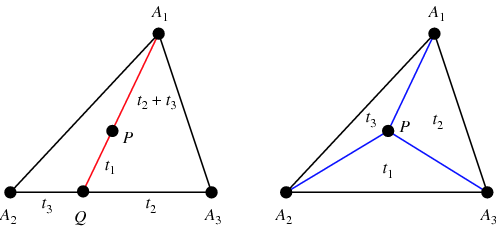
Barycentric

Aby znaleźć współrzędne barycentryczne dla dowolnego punktu P, znajdź t_2 i t_3 z punktu Q w punkcie przecięcia prostej A_1P z bokiem A_2A_3, a następnie wyznaczamy t_1 jako masę w punkcie A_1, która zrównoważy masę t_2+t_3 w punkcie Q, czyniąc tym samym P centroidem (lewy rysunek). Ponadto, pola trójkątów DeltaA_1A_2P, DeltaA_1A_3P, i DeltaA_2A_3P są proporcjonalne do współrzędnych barycentrycznych t_3, t_2, i t_1 z P (prawy rysunek; Coxeter 1969, s. 217).

Współrzędne barycentryczne są jednorodne, więc

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

dla mu!=0.

Współrzędne barycentryczne znormalizowane tak, że stają się rzeczywistymi powierzchniami podtrójkątów nazywamy jednorodnymi współrzędnymi barycentrycznymi. Współrzędne barycentryczne znormalizowane tak, że

t_1+t_2+t_3=1,
(2)

tak, że współrzędne te dają pola podtrójkątów znormalizowane przez pole pierwotnego trójkąta nazywamy współrzędnymi arealnymi (Coxeter 1969, s. 218). Współrzędne barycentryczne i arealne mogą dostarczyć szczególnie eleganckich dowodów twierdzeń geometrycznych, takich jak twierdzenie Routha, twierdzenie Cevy i twierdzenie Menelaosa (Coxeter 1969, s. 219-221).

(Niekoniecznie jednorodne) współrzędne barycentryczne dla kilku popularnych ośrodków są podsumowane w poniższej tabeli. W tabeli, a, b, i c są długościami boków trójkąta, a s jest jego półmetkiem.

środek trójkąta współrzędne bariocentryczne
obwód O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
punkt Gergonne’a Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
punkt Nagela Na (s-a,s-b,s-c)
ortocentrum H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symediana punktu K (a^2,b^2,c^2)
centroid trójkąta G (1,1,1)

Wewspółrzędnych barycentrycznych prosta ma liniowe równanie jednorodne. W szczególności, prosta łącząca punkty (r_1,r_2,r_3) i (s_1,s_2,s_3) ma równanie

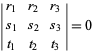|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 i 57; Coxeter 1969, s. 219; Bottema 1982). Jeśli wierzchołki P_i trójkąta DeltaP_1P_2P_3 mają współrzędne barycentryczne (x_i,y_i,z_i), to pole trójkąta wynosi

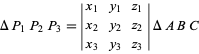DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Dodaj komentarz