Um autômato celular é uma coleção de células “coloridas” em uma grade de forma especificada que evolui através de uma série de passos de tempo discretos de acordo com um conjunto de regras baseadas nos estados das células vizinhas. As regras são então aplicadas iterativamente por quantos passos de tempo desejar. von Neumann foi uma das primeiras pessoas a considerar tal modelo, e incorporou um modelo celular ao seu “construtor universal”. Autômatos celulares foram estudados no início dos anos 50 como um possível modelo para sistemas biológicos (Wolfram 2002, p. 48). Estudos abrangentes sobre autômatos celulares foram realizados por S. Wolfram a partir dos anos 80, e a pesquisa fundamental da Wolfram no campo culminou com a publicação de seu livro A New Kind of Science (Wolfram 2002), no qual Wolfram apresenta uma gigantesca coleção de resultados sobre autômatos, entre os quais se destacam uma série de novas descobertas revolucionárias.
O episódio da temporada 2 “Bettor or Worse” (2006) do drama de crime televisivo NUMB3RS menciona autômatos celulares unidimensionais.
Os autômatos celulares vêm em uma variedade de formas e variedades. Uma das propriedades mais fundamentais de um autômato celular é o tipo de grade sobre a qual ele é computado. A mais simples “grelha” é uma linha unidimensional. Em duas dimensões, grades quadradas, triangulares e hexagonais podem ser consideradas. Autômatos celulares também podem ser construídos em grades cartesianas em números arbitrários de dimensões, sendo a malha inteira 
-dimensional 
a escolha mais comum. Autômatos celulares em uma malha inteira 
-dimensional são implementados na Wolfram Language como CellularAutomaton.
O número de cores (ou estados distintos) 
um autômato celular também pode assumir que deve ser especificado. Este número é tipicamente um inteiro, com 
(binário) sendo a escolha mais simples. Para um autômato binário, a cor 0 é comumente chamada de “branco”, e a cor 1 é comumente chamada de “preto”. Entretanto, autômatos celulares com uma faixa contínua de valores possíveis também podem ser considerados.
Além da grade na qual um autômato celular vive e as cores que suas células podem assumir, a vizinhança sobre a qual as células afetam umas às outras também deve ser especificada. A escolha mais simples é “vizinhos mais próximos”, em que apenas as células diretamente adjacentes a uma determinada célula podem ser afetadas a cada passo. Dois bairros comuns no caso de um autômato celular bidimensional em uma grade quadrada são o chamado bairro Moore (um bairro quadrado) e o bairro von Neumann (um bairro em forma de diamante).
O tipo mais simples de autômato celular é um autômato unidimensional binário, vizinho mais próximo. Tais autômatos foram chamados de “autômatos celulares elementares” por S. Wolfram, que estudou extensivamente suas incríveis propriedades (Wolfram 1983; 2002, p. 57). Existem 256 desses autômatos, cada um dos quais pode ser indexado por um número binário único cuja representação decimal é conhecida como a “regra” para o autômato particular. Uma ilustração da regra 30 é mostrada acima junto com a evolução que ela produz após 15 passos a partir de uma única célula preta.
Uma classe um pouco mais complicada de autômatos celulares são os mais próximos do vizinho, 
autômatos celulares totalistas unidimensionais, coloridos. Em tais autômatos, é a média das células adjacentes que determinam a evolução, e os exemplos não triviais mais simples têm 
cores. Para estes autômatos, o conjunto de regras que descrevem o comportamento pode ser codificado como um 
-dígito 
-um número fixo, conhecido como “código”. As regras e 300 passos do ternário (
) código 912 autômato são ilustradas acima.
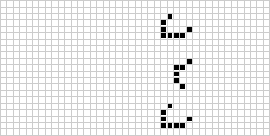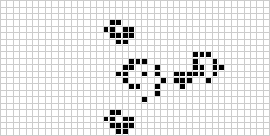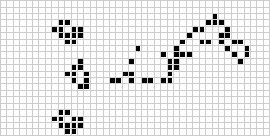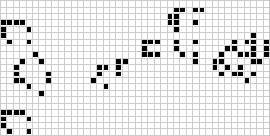
Em duas dimensões, o autômato celular mais conhecido é o jogo da vida de Conway, descoberto por J. H. Conway em 1970 e popularizado nas colunas Scientific American de Martin Gardner. O jogo da vida é um binário (
) autômato celular totalista com uma vizinhança Moore de alcance 
. Embora o cálculo das sucessivas gerações do jogo da vida tenha sido feito originalmente à mão, a revolução do computador logo chegou e permitiu que padrões mais extensos fossem estudados e propagados. Uma animação do jogo de construção da vida conhecida como um trem de puffer é ilustrada acima.
WireWorld é outro jogo de autômato celular bidimensional comum.
A teoria dos autômatos celulares é imensamente rica, com regras e estruturas simples sendo capazes de produzir uma grande variedade de comportamentos inesperados. Por exemplo, existem autômatos celulares universais que são capazes de simular o comportamento de qualquer outro autômato celular ou máquina Turing. Foi mesmo provado por Gacs (2001) que existem autômatos celulares universais tolerantes a falhas, cuja capacidade de simular outros autômatos celulares não é prejudicada por perturbações aleatórias, desde que tais perturbações sejam suficientemente esparsas.