>
Biografia
 >
>
Brahmagupta (598-668 CE)
>
O grande matemático e astrônomo indiano do século VII Brahmagupta escreveu alguns trabalhos importantes sobre matemática e astronomia. Ele era do estado de Rajasthan do noroeste da Índia (ele é frequentemente referido como Bhillamalacarya, o professor de Bhillamala), e mais tarde tornou-se o chefe do observatório astronômico em Ujjain, no centro da Índia. A maioria de suas obras são compostas em verso elíptico, uma prática comum na matemática indiana da época, e conseqüentemente têm algo de poético em seu anel.
Parece provável que as obras de Brahmagupta, especialmente o seu texto mais famoso, o “Brahmasphutasiddhanta”, foram trazidas pelo califa Abbasid Al-Mansur do século VIII ao seu recém fundado centro de aprendizagem em Bagdá, às margens do Tigre, proporcionando uma importante ligação entre a matemática e a astronomia indiana e a nascente ascensão da ciência e da matemática no mundo islâmico.
No seu trabalho sobre aritmética, Brahmagupta explicou como encontrar o cubo e a raiz cúbica de um inteiro e deu regras que facilitam o cálculo de quadrados e raízes quadradas. Ele também deu regras para lidar com cinco tipos de combinações de frações. Ele deu a soma dos quadrados dos primeiros n números naturais como n(n + 1)(2n + 1)⁄ 6 e a soma dos cubos dos primeiros n números naturais como (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Tratar o zero como um número

>
Brahmagupta’s rules for dealing with zero and negative numbers
Brahmagupta’s genius, though, came in his treatment of the concept of (then relativamente new) the number zero. Embora muitas vezes também atribuído ao matemático indiano Bhaskara I do século VII, seu “Brahmasphutasiddhanta” é provavelmente o mais antigo texto conhecido para tratar o zero como um número por direito próprio, em vez de ser simplesmente um dígito de lugar como foi feito pelos babilônios, ou como um símbolo de falta de quantidade como foi feito pelos gregos e romanos.
Brahmagupta estabeleceu as regras matemáticas básicas para lidar com zero (1 + 0 = 1; 1 – 0 = 1; e 1 x 0 = 0), embora seu entendimento da divisão por zero fosse incompleto (ele pensou que 1 ÷ 0 = 0). Quase 500 anos depois, no século XII, outro matemático indiano, Bhaskara II, mostrou que a resposta deveria ser infinito, e não zero (com o argumento de que 1 pode ser dividido em um número infinito de peças de tamanho zero), uma resposta que foi considerada correta por séculos. No entanto, esta lógica não explica porque 2 ÷ 0, 7 ÷ 0, etc, também deveria ser zero – a visão moderna é que um número dividido por zero é na verdade “indefinido” (ou seja, não faz sentido).
Brahmagupta vê os números como entidades abstratas, em vez de apenas para contar e medir, o que lhe permitiu dar mais um enorme salto conceitual que teria consequências profundas para a matemática futura. Anteriormente, a soma 3 – 4, por exemplo, era considerada sem sentido ou, na melhor das hipóteses, apenas zero. Brahmagupta, no entanto, percebeu que poderia haver uma coisa como um número negativo, que ele chamou de “dívida” em oposição a “propriedade”. Ele expôs as regras para lidar com números negativos (por exemplo, um negativo vezes um negativo é um positivo, um negativo vezes um positivo é um negativo, etc).
Outras vezes, ele apontou, equações quadráticas (do tipo x2 + 2 = 11, por exemplo) poderiam em teoria ter duas soluções possíveis, uma das quais poderia ser negativa, porque 32 = 9 e -32 = 9. Além de seu trabalho em soluções para equações lineares gerais e equações quadráticas, Brahmagupta foi ainda mais longe ao considerar sistemas de equações simultâneas (conjunto de equações contendo múltiplas variáveis), e resolver equações quadráticas com duas incógnitas, algo que só foi considerado no Ocidente mil anos depois, quando Fermat estava considerando problemas semelhantes em 1657.
Teoria de Brahmagupta sobre quadriláteros cíclicos
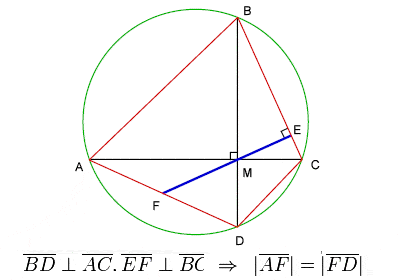
Teoria de Brahmagupta sobre quadriláteros cíclicos
Brahmagupta até mesmo tentou escrever estes conceitos bastante abstratos, usando as iniciais dos nomes das cores para representar incógnitas nas suas equações, uma das primeiras intimações do que hoje conhecemos como álgebra.
Brahmagupta dedicou uma parte substancial do seu trabalho à geometria e trigonometria. Ele estabeleceu √10 (3.162277) como uma boa aproximação prática para π (3.141593), e deu uma fórmula, agora conhecida como Fórmula de Brahmagupta, para a área de um quadrilátero cíclico, bem como um célebre teorema nas diagonais de um quadrilátero cíclico, geralmente referido como Teorema de Brahmagupta.
| << De volta à Matemática Indiana | > Avançar para Madhava >>> |