Coordenadas Baricêntricas são triplos de números 
correspondente às massas colocadas nos vértices de um triângulo de referência 
. Estas massas determinam então um ponto 
, que é o centróide geométrico das três massas e é identificado com coordenadas 
. Os vértices do triângulo são dados por 
, 
, e 
. As coordenadas baricêntricas foram descobertas por Möbius em 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
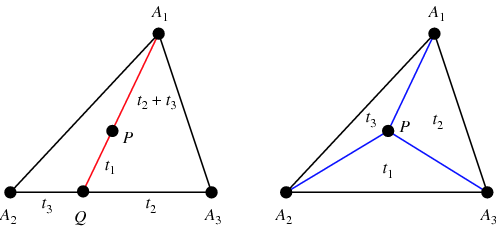
Para encontrar as coordenadas baricêntricas para um ponto arbitrário 
, encontrar 
e 
do ponto 
na intersecção da linha 
com o lado 
, e depois determinar 
como a massa em 
que irá equilibrar uma massa 
em 
, fazendo assim 
o centróide (figura à esquerda). Além disso, as áreas dos triângulos 
, 
, e 
são proporcionais às coordenadas baricêntricas 
, 
, e 
de 
(figura à direita; Coxeter 1969, p. 217).
Barycentric coordinates are homogeneous, so
 |
(1)
|
for 
.
Coordenadas baricêntricas normalizadas para que se tornem as áreas reais dos subtriângulos são chamadas de coordenadas baricêntricas homogêneas. As coordenadas baricêntricas normalizadas de modo que
 |
(2)
|
de modo que as coordenadas dão as áreas dos subtriângulos normalizados pela área do triângulo original são chamadas de coordenadas areais (Coxeter 1969, p. 218). As coordenadas baricêntricas e areais podem fornecer provas particularmente elegantes de teoremas geométricos como o teorema de Routh, o teorema de Ceva e o teorema de Menelaus (Coxeter 1969, pp. 219-221).
(Não necessariamente homogêneo) as coordenadas baricêntricas para um número de centros comuns estão resumidas na tabela seguinte. Na tabela, 
, 
, e 
são os comprimentos laterais do triângulo e 
é o seu semiperímetro.
| centro do triângulo | coordenadas bari-cêntricas |
circuncentro  |
( ,  ,  ) |
excenter  |
 |
excenter  |
 |
excenter  |
 |
| Ponto de Gergonne Ge | ( ,  ,  ) |
incinerador  |
 |
| Nagel point Na |  |
orthocenter  |
( ,  ,  ) |
ponto simédrico  |
 |
centroide triangular  |
 |
Em coordenadas baricêntricas, uma linha tem uma equação linear homogênea. Em particular, os pontos de união de linhas 
e 
tem a equação
 |
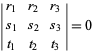(3)
|
(Loney 1962, pp. 39 e 57; Coxeter 1969, p. 219; Bottema 1982). Se os vértices 
de um triângulo 
têm coordenadas baricêntricas 
, então a área do triângulo é
 |
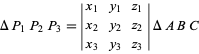(4)
|
(Bottema 1982, Yiu 2000).