Factor de compressibilidade (gases) - Knowino

From Knowino

Esta é uma versão verificada desta página

Pule para: navegação,pesquisa

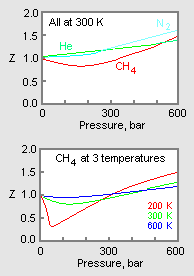
Figure 1: Exemplo de gráficos de factores de compressibilidade de gás

O factor de compressibilidade (Z) é uma propriedade termodinâmica útil para modificar a lei de gás ideal para ter em conta o comportamento de gases reais. É uma medida de quanto as propriedades termodinâmicas de um gás real se desviam daquelas esperadas de um gás ideal. Pode ser pensado como a razão entre o volume real de um gás real e o volume previsto pelo gás ideal à mesma temperatura e pressão que o volume real.

Para um gás ideal, Z tem sempre um valor de 1. Para gases reais, o valor pode divergir positivamente ou negativamente, dependendo do efeito das forças intermoleculares do gás. Quanto mais próximo um gás real estiver do seu ponto crítico ou do seu ponto de saturação, maiores são os desvios do gás do comportamento ideal.

O gráfico superior da Figura 1 ilustra como o fator de compressibilidade varia para diferentes gases à mesma temperatura e pressão. O gráfico inferior ilustra como o fator de compressibilidade de um gás (por exemplo, metano) a uma determinada pressão varia com a temperatura.

Este artigo trata apenas do fator de compressibilidade dos gases e não aprofunda na compressibilidade de líquidos ou misturas vapor-líquido.

Conteúdo

1 Determinação dos valores de compressibilidade dos gases
- 1.1 Gráficos de fatores de compressibilidade generalizada para gases puros
- 1.2 Gráficos de fatores de compressibilidade generalizada para misturas gasosas
- 1.3 A equação van der Waals
  - 1.3.1 Versões modificadas da equação van der Waals
    - 1.3.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Equação virial de estado
- 1.5 Outras equações de estado
- 1.6 Notação para a constante de gás
2 Referências

Determinação dos valores de compressibilidade do gás

A lei do gás ideal é definida como:

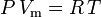
$P\,V_\mathrm{m} = R\,T$

e a lei de gás ideal corrigida por não-idealidade é definida como:

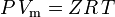
$P\,V_\mathrm{m} = ZR\,T$

onde:
P	= pressão
Vm	= volume molar do gás
Z	= factor de compressibilidade
R	= Constante de gás universal
T	= temperatura

e assim:

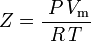
$Z = \frac{\;P\,V_\mathrm{\}}{R\,T}$

que é a mais simples e mais amplamente utilizada equação de estado de gás real (EOS). A maior limitação desta equação de estado é que o fator de compressibilidade do gás, Z, não é uma constante, mas varia de um gás para outro, bem como com a temperatura e pressão do gás em consideração. Deve ser determinado experimentalmente.

Onde dados experimentais estão disponíveis para gases específicos, esses dados podem ser usados para produzir gráficos (como na Figura 1) de Z versus pressão a uma temperatura constante ou de Z versus pressão para várias temperaturas para esses gases específicos. Tais gráficos são úteis para obter prontamente valores interpolados de Z entre os valores determinados experimentalmente.

O fator de compressibilidade, como mencionado anteriormente, também pode ser expresso como:

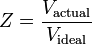
$Z = \frac{V_\mathrm{actual}}{V_\mathrm{ideal}}$

Existem três regimes que afetam o fator de compressibilidade:

o valor de Z tende para 1 à medida que a pressão do gás se aproxima de 0, onde todos os gases tendem ao comportamento ideal
o valor de Z é inferior a 1 a pressões intermediárias porque as forças intermoleculares de atração fazem com que os volumes reais sejam menores que os valores ideais
o valor de Z é maior que 1 e por fim tende ao infinito a pressões elevadas porque as forças repulsivas intermoleculares fazem com que os volumes reais sejam superiores aos valores ideais

Gráficos de factores de compressibilidade generalizados para gases puros

A relação única entre o factor de compressibilidade e a temperatura reduzida, Tr, e a pressão reduzida, Pr, foi reconhecida pela primeira vez por van der Waals em 1873 e é conhecida como o princípio dos dois parâmetros dos estados correspondentes. O princípio dos estados correspondentes expressa a generalização de que as propriedades de um gás que dependem de forças intermoleculares estão relacionadas com as propriedades críticas do gás de uma forma universal. Isso fornece uma base mais importante para o desenvolvimento de correlações de propriedades moleculares.

Como para a compressibilidade dos gases, o princípio dos estados correspondentes indica que qualquer gás puro à mesma temperatura reduzida, Tr, e pressão reduzida, Pr, deve ter o mesmo fator de compressibilidade.

A temperatura e pressão reduzidas são definidas como:

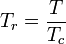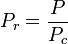
$T_r = \frac{T}{T_c}$ e $P_r = \frac{P}{P_c}$

Tc e Pc são conhecidas como a temperatura e pressão críticas de um gás. São características de cada gás específico, sendo Tc a temperatura acima da qual não é possível liquidificar um determinado gás e Pc a pressão mínima necessária para liquidificar um determinado gás à sua temperatura crítica. Juntos eles definem o ponto crítico de um fluido acima do qual não existem fases líquidas e gasosas distintas de um determinado fluido.

Os dados de pressão-volume-temperatura (PVT) para gases reais variam de um gás puro para outro. Entretanto, quando os fatores de compressibilidade de vários gases monocomponentes são comprimidos versus pressão juntamente com isotermas de temperatura (como mostrado para o metano no gráfico inferior da Figura 1), muitos dos gráficos exibem formas isotérmicas semelhantes.

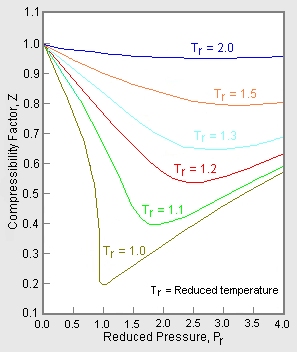
Figure 2: Exemplo de um gráfico de fator de compressibilidade generalizado

Para obter um gráfico generalizado que pode ser usado para muitos gases diferentes, a pressão e temperatura reduzidas, Pr e Tr, são usados para normalizar os dados do fator de compressibilidade. A Figura 2 é um exemplo de um gráfico generalizado do fator de compressibilidade derivado de centenas de pontos de dados experimentais P-V-T de 10 gases puros, a saber, metano, etano, etileno, propano, n-butano, i-pentano, n-hexano, nitrogênio, dióxido de carbono e vapor.

Existem gráficos mais detalhados de factores de compressibilidade generalizados baseados em 25 ou mais gases puros diferentes, tais como os gráficos de Nelson-Obert. Diz-se que tais gráficos têm uma precisão de 1-2 por cento para valores Z superiores a 0,6 e de 4-6 por cento para valores Z de 0,3-0,6,

Os gráficos do fator de compressibilidade generalizado podem estar consideravelmente em erro para gases fortemente polares que são gases para os quais os centros de carga positiva e negativa não coincidem. Nesses casos, a estimativa para Z pode estar em erro em até 15-20 por cento.

Os gases quânticos hidrogênio, hélio e neônio não estão de acordo com o comportamento dos estados correspondentes e a pressão e temperatura reduzidas para esses três gases devem ser redefinidas da seguinte forma para melhorar a precisão da previsão de seus fatores de compressibilidade ao utilizar os gráficos generalizados:

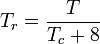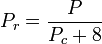
$T_r = \frac{T}{T_c + 8}$ e $P_r = \frac{P}{P_c + 8}$

onde as temperaturas estão em graus Kelvin e as pressões estão em atmosferas.

Gráficos de fator de compressibilidade generalizada para misturas gasosas

Gráficos de fator de compressibilidade generalizada para gases puros (como exemplificado na Figura 2 ou nos gráficos de Nelson-Obert também podem ser utilizados para misturas gasosas utilizando a Regra de Kay proposta por W. B. Kay em 1936. Essa regra prevê o comportamento de P-V-T de uma mistura gasosa determinando o fator de compressibilidade de uma mistura gasosa à temperatura reduzida e à pressão reduzida definida em termos de temperatura pseudocrítica, Tpc e pressão pseudocrítica, Ppc que são definidos como:

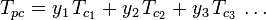
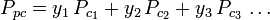
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3},{c_3},{dots$ $P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3},{c_3},{c_3}dots$

where:
Tpc	= a temperatura pseudocrítica da mistura de gás
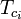$T_{c_i}$	= a temperatura crítica de um componente da mistura gasosa
Ppc	= o pseudocrítico pressão da mistura de gás
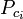$P_{c_i}$	= a temperatura crítica de um componente do gás
yi	= a fracção molar (ou volume) de um componente do gás

a temperatura pseudoduzida, Tpr, e a pressão pseudoduzida, Ppr, para usar com os gráficos de fator de compressibilidade generalizada para gases puros são então:

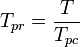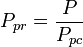
$T_{pr} = \frac{T}{T_{pc}}$ e $P_{pr} = \frac{P}{P_{pc}}$

Um gráfico de fator de compressibilidade para gás natural (que é uma mistura de hidrocarbonetos e outros gases) usando temperaturas e pressões pseudoduzidas está disponível na Internet.

A equação van der Waals

A equação van der Waals foi desenvolvida em 1873 e pode ser expressa como:

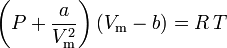
$esquerda(P + \frac{a}{V_\mathrm{m}^2}{direita){esquerda(V_\mathrm{m} - b\direita) = R\,T$

em qualquer lugar:

a é uma medida da força de atração entre as moléculas de gás b contabiliza o volume ocupado pelas moléculas de gás, o que diminui o volume aberto disponível

A equação van der Waals pode ser re-arranjada como:

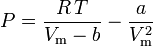
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

e o factor de compressibilidade pode ser escrito como:

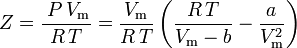
$Z = {\an8}frac{\an8}P\,V_mathrm{m}{R\,T} = {V_mathrm{m}}{R\,T}esquerda(V_mathrm{R\,T}{V_mathrm{m} - b} - {V_mathrm{m}^2}{V_mathrm{m}}$

e agora temos uma equação para determinar Z usando os parâmetros van der Waals a e b:

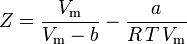
$Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}$

Embora a e b sejam referidas como “as constantes Van der Waals”, elas não são verdadeiramente constantes porque variam de um gás para outro; são, no entanto, independentes de P, V e T. Em outras palavras, elas são constantes para o gás a ser considerado. Dada a temperatura e pressão críticas para um gás específico, a e b podem ser obtidas para esse gás específico a partir destas equações:

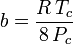
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ e $b = \frac{R\, T_c}{8\, P_c}$

Por exemplo, a pressão crítica do etano é 4.884 MPa e a temperatura crítica é de 305,43 K (32.3˚C). Usando a constante universal do gás, R, de 8,3145 Pa m3 K-1 mol-1, as equações acima produzem a = 0,557 m6 Pa mol-2 e b = 6,500×10-5 m3 mol-1,

Valores tabulados de a e b para vários gases estão disponíveis nestas referências, assim como muitas outras fontes na literatura técnica.

Versões modificadas da equação van der Waals

Determinar fatores de compressibilidade usando a equação de estado de van der Waals é uma melhoria em relação ao uso dos gráficos de compressibilidade generalizada. No entanto, existem versões modificadas da equação de estado de van der Waals que proporcionam ainda mais melhorias. Talvez as equações de estado mais usadas pelos engenheiros que trabalham na refinação de petróleo, produção petroquímica, processamento de gás natural, destilação criogênica e indústrias relacionadas sejam: a equação de Redlich-Kwong desenvolvida em 1949, a equação de Soave-Redlich-Kwong desenvolvida em 1972 e a equação de Peng-Robinson desenvolvida em 1976. Essas três equações são essencialmente versões modificadas da equação de van der Waals. As equações comparativas são:

Redlich-Kwong

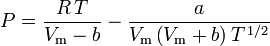
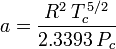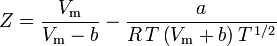
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}}{V_\mathrm esquerda(V_\mathrm {m} + b=direita)T^{\,1/2}}$ $a = \frac{R^2}, T_c^{\,5/2}}{2.3393\, P_c}$ e $b = {R^2}, T_c}{11.5420, P_c}$ $Z = |frac{V_mathrm{m}}{V_mathrm{m} - b} - |frac{a}{R, T_left(V_)mathrm {m} + b) right)T^{\i1} T^{\i1},1/2}}$

Soave-Redlich-Kwong

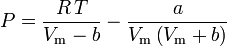
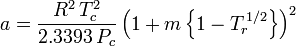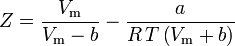
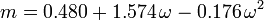
$P = {R=frac{R\,T}{V_\mathrm{m} - b} - {V_\mathrm{a}{V_\mathrm{mathrm{m} -esquerda(V_\athrm} + b=direita)}$ $a = {R^2\,T_c^2}{2.3393,P_c, Big(1 + m), Big(1 - T_r^,1/2} {\i1}Big)^2$ e $b = |frac{R^, T_c}{11.5420, P_c}$ $Z = {V_mathrm{m}}{V_mathrm{m} - b} - {R}, T_frac{a}{R, T_left(V_\mathrm {m} + b) direita)}$ $m = 0.480 + 1,574, {\i1}-omega - 0,176}, {\i1}mega^2$

O fator concêntrico, ω, usado como parâmetro nas equações de Soave-Redlich-Kwong e Peng-Robinson foi introduzido pela primeira vez por Pitzer et al em 1955. Ele pode ser expresso como:

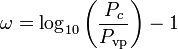
$\omega = \log_{10} \esquerda(P_c}{P_c}{P_mathrm{vp}}direita) - 1$

onde Pvp é a pressão de vapor saturado do gás a uma temperatura de 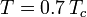$T = 0.7\, T_c$ .

Peng-Robinson

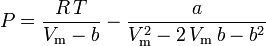
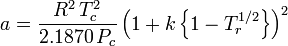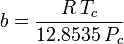
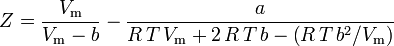
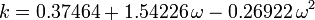
$P = {R\\,T}{V_\mathrm{m} - b} - {V_\mathrm{m}^2 - 2\,V_\mathrm{m}, b - b^2}$ $a = {R\\,T_c^2}{2.1870, P_c, Big(1 + k), Big(1 - T_r^{1/2}Big)^2$ e $b = {R, T_c}{12.8535}, P_c}$ $Z = {V_mathrm{m}}{V_mathrm{m} - b} -frac{a}{R,T,V_mathrm{m} + 2\,R\,T\,b - esquerda(R\,T\,b^2/V_mathrm{m}{m}direita)}$ $k = 0,37464 + 1,54226\, \i>0,26922\, \i>2$

Equação de estado virial

A equação de estado mais fundamental, na medida em que tem a base teórica mais sólida, é a equação de estado virial:

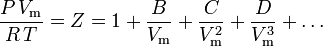
> $\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} +frac{C}{V_mathrm{m}^2} +frac{D}{V_mathrm{m}^3} \\i1$

Foi proposto pela primeira vez de forma empírica por Thiesen em 1885 e desenvolvido em 1901 por Kamerlingh-Onnes. Uma expressão estatística-mecânica para B foi derivada pela primeira vez por Ornstein em sua tese de doutorado. A equação foi posteriormente re-desenvolvida por H. D. Ursell em 1927 com base teórica derivada de uma análise estatística-mecânica (cluster) de forças intermoleculares.

Os parâmetros B, C e D são referidos como o segundo, terceiro e quarto coeficientes virais, respectivamente. Os coeficientes não são constantes, pois variam de um gás para outro, bem como a temperatura do gás em consideração. Por vezes são escritos como B(T), C(T) e D(T) para denotar que são funções da temperatura. O valor numérico dos coeficientes deve ser determinado experimentalmente.

O segundo coeficiente virial fornece a maior parte da correção para o comportamento não-ideal de um gás. Por essa razão, a equação virial é por vezes truncada após o termo contendo o segundo coeficiente. Entretanto, quando o terceiro coeficiente está disponível, a equação geralmente é truncada após o termo que contém o terceiro coeficiente. O quarto coeficiente é raramente disponível.

Uma extensa compilação de coeficientes virais para gases puros e misturas de gases foi preparada a partir da base de dados de coeficientes virais no Thermodynamics Research Center, anteriormente na Texas A&M University, College Station, Texas e agora localizada no National Institute of Standards and Technology (NIST), Boulder, Colorado. A última versão dessa compilação foi publicada em 2003. NIST também oferece para compra um programa de software, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), que inclui o segundo e terceiro coeficientes viriais, bem como uma série de outras propriedades termodinâmicas.

Outras equações de estado

Existem várias outras equações de estado para prever o comportamento de gases reais. Talvez, as mais conhecidas sejam a equação Beattie-Bridgeman desenvolvida em 1929 e a equação Benedict-Rubin-Webb desenvolvida em 1940. Em geral, elas são mais complexas que as equações discutidas acima.

Notação para a constante gasosa

A constante gasosa utilizada neste artigo é a constante gasosa universal, R, que se aplica a qualquer gás. Há também uma constante gasosa específica, que pode ser designada como Rs, e é definida como Rs = R / M onde M é o peso molecular.

Felizmente, muitos autores na literatura técnica às vezes usam R como constante gasosa específica, sem a designar como tal ou afirmar que é a constante gasosa específica. Isto pode e leva a confusão.

1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. e Simon, John D. (1999). Termodinâmica Molecular. Livros de Ciências Universitárias. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal e Robert H. Turner (2004). Fundamentos das Ciências Termal-Fluídas, 2ª Edição. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.3 3.4 Smith, J.M. et al. (2005). Introdução à Termodinâmica de Engenharia Química, Sétima Edição. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.4 4.5 4.6 Y.V.C. Rao (1997). Termodinâmica de Engenharia Química. Imprensa Universitária (Índia). ISBN 81-7371-048-1.
5.0 5.1 Leis de Gás (Palestra do Professor M.J. Mombourquette na Queens University, Canadá)
Hong Wei Xiang (2005). O Princípio dos Estados Correspondentes e sua Prática: Termodinâmica, Transporte e Propriedades de Superfície dos Fluidos. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). “Lei Modificada dos Estados Correspondentes”. Industrial & Química de Engenharia 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Equações de Estado (Professor Lyes Kadem, Concordia University, Canadá)
10.0 10.1 Equações de Estado (Material de Palestra usado pelo Professor Sanford Klein na Universidade de Wisconsin-Madison, EUA)
Richard W. Miller (1996). Flow Measurement Engineering Handbook (Manual de Engenharia de Medição de Fluxo), 3ª Edição. McGraw-Hill. ISBN 0-07-042366-0. (Veja Figura G-1 na página G.145)
Kai-Fui Vincent Wong (2000). Termodinâmica para Engenheiros, 1ª Edição. CRC Press. ISBN 0-8493-0232-3. (Veja Figura A-2, Página 278}
Nelson-Obert Generalized Compressibility Charts (Gráficos disponíveis na Internet, do site da San Diego State University, EUA)
W.B.Kay (1936). “Gases e Vapores a Alta Temperatura e Pressão – Densidade de Hidrocarboneto”. Engenharia Industrial & Química 28:1014. ISSN 0096-4484.
Yunus A. Çengal e Michael A. Bowes (2005). Termodinâmica: An Engineering Approach, 5ª Edição. McGraw-Hill. ISBN 0-07-2884959.
Gases Reais (Material de Palestra usado pelo Professor R.M. Price na Universidade Christian Brothers, EUA)
Propriedades dos Gases Naturais (Professor Jon Steiner Gudmandsson, Universidade Norueguesa de Ciência e Tecnologia)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
19,0 19,1 19,2 Capítulo 3: Equações de Estado (páginas 6-8 de 65 páginas pdf) (Parte da tese de doutorado de Ji Lin Wang, 2002, Swinbourne University of Technology, Austrália)
20,0 20,1 20,2 Jean Vidal (2003). Termodinâmica: Aplicações em Engenharia Química e na Indústria do Petróleo. Edições Technip. ISBN 2-7108-0800-5.
Zakia Nasri e Housam Binous (2007). “Aplicações da Equação de Estado Soave-Redlich-Kwong usando Mathematica”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Obtido a partir daqui.
K.S. Pitzer et al (1955). “The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning e Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Definição de Fator Acêntrico (Physical Property Sources Index, PPSI, do Instituto Federal Suíço de Tecnologia de Zurique)
Max F. Thiesen (1885). “Investigations of the Equation of State” (Investigações da Equação de Estado). Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). “Expressão da Equação de Estado de Gases e Líquidos por Meios de Série”. Comun. Laboratório de Física. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Aplicação da mecânica estatística de Gibbs sobre problemas de teoria molecular), Leiden
H. D. Ursell (1927). “The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
J. D. Dymond e R. C. Wilhoit (Autores), K. N. Marsch e M. Fenkel (Editores) (2003). Virial Coefficients of Pure Gas and Mixtures, 1ª Edição. Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie e O.C. Bridgeman (1929). “A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb e L.C. Rubin (1940). “An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.

Alguns conteúdos desta página podem ter aparecido anteriormente em Citizendium.

Retrieved from “http://knowino.org/wiki/Compressibility_factor_(gases)”

Categoria: Física