Uma matriz de confusão é uma tabela que é frequentemente usada para descrever o desempenho de um modelo de classificação (ou “classificador”) num conjunto de dados de teste para os quais os valores verdadeiros são conhecidos. A matriz de confusão em si é relativamente simples de entender, mas a terminologia relacionada pode ser confusa.
Queria criar um “guia de referência rápida” para a terminologia da matriz de confusão porque não consegui encontrar um recurso existente que se adequasse aos meus requisitos: compacto na apresentação, usando números em vez de variáveis arbitrárias, e explicado tanto em termos de fórmulas como de frases.
>
Demos começar com um exemplo de matriz de confusão para um classificador binário (embora possa ser facilmente estendida ao caso de mais de duas classes):
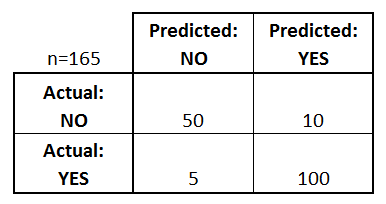
O que podemos aprender com esta matriz?
- Existem duas possíveis classes previstas: “sim” e “não”. Se estivéssemos prevendo a presença de uma doença, por exemplo, “sim” significaria que eles têm a doença, e “não” significaria que eles não têm a doença.
- O classificador fez um total de 165 previsões (por exemplo, 165 pacientes estavam sendo testados para a presença dessa doença).
- Desses 165 casos, o classificador previu “sim” 110 vezes, e “não” 55 vezes.
- Na realidade, 105 pacientes da amostra têm a doença, e 60 pacientes não têm.
Vamos agora definir os termos mais básicos, que são números inteiros (não taxas):
- verdadeiros positivos (TP): Estes são casos em que nós previmos sim (eles têm a doença), e eles têm a doença.
- verdadeiros negativos (TN): Nós previmos não, e eles não têm a doença.
- falsos positivos (PF): Nós previmos que sim, mas eles não têm a doença. (Também conhecido como “erro de Tipo I”)
- falsos negativos (FN): Nós previmos que não, mas eles realmente têm a doença. (Também conhecido como um “erro Tipo II”)
Adicionei estes termos à matriz de confusão, e também adicionei os totais de linhas e colunas:
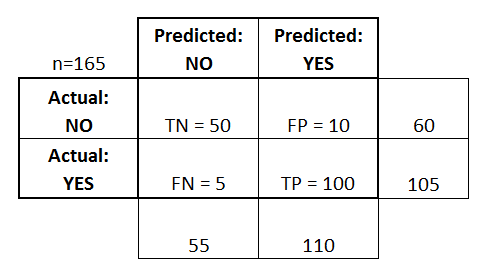
Esta é uma lista de taxas que são frequentemente calculadas a partir de uma matriz de confusão para um classificador binário:
- Precisão: Em geral, com que frequência o classificador é correto?
- (TP+TN)/total = (100+50)/165 = 0,91
- Taxa de erro de classificação: Em geral, com que frequência é errado?
- (FP+FN)/total = (10+5)/165 = 0,09
- equivalente a 1 menos Precisão
- também conhecido como “Taxa de Erro”
- Taxa Positiva Verdadeira: Quando é realmente sim, com que frequência prevê sim?
- TP/actual sim = 100/105 = 0.95
- também conhecido como “Sensibilidade” ou “Relembrar”
- Taxa Positiva Falsa: Quando na verdade é não, quantas vezes prevê sim?
- FP/actual não = 10/60 = 0,17
- Taxa Negativa Verdadeira: Quando na verdade é não, quantas vezes prevê não?
- TN/actual não = 50/60 = 0,83
- equivalente a 1 menos a Falsa Taxa Positiva
- também conhecida como “Especificidade”
- Precisão: Quando prevê sim, com que frequência é correcto?
- TP/previsto sim = 100/110 = 0,91
- Prevalência: Com que frequência a condição de sim realmente ocorre em nossa amostra?
- actual sim/total = 105/165 = 0,64
>
Outros termos também são dignos de menção:
- Taxa de erro nula: Esta é a frequência com que você estaria errado se você sempre previu a classe majoritária. (No nosso exemplo, a taxa de erro nula seria 60/165=0,36 porque se você sempre previu que sim, você só estaria errado para os 60 casos “não”). Esta pode ser uma métrica de base útil para comparar o seu classificador com o seu. No entanto, o melhor classificador para uma determinada aplicação terá, por vezes, uma taxa de erro superior à taxa de erro nulo, como demonstrado pelo Paradoxo de Precisão.
- Kappa de Cohen: Esta é essencialmente uma medida de quão bem o classificador funcionava em comparação com o quão bem teria funcionado simplesmente por acaso. Em outras palavras, um modelo terá uma alta pontuação Kappa se houver uma grande diferença entre a precisão e a taxa de erro nula. (Mais detalhes sobre a Kappa de Cohen.)
- F Pontuação: Esta é uma média ponderada da verdadeira taxa positiva (recall) e precisão. (Mais detalhes sobre a Pontuação F.)
- Curva ROC: Este é um gráfico comumente usado que resume o desempenho de um classificador em todos os limites possíveis. Ele é gerado através da plotagem da Taxa Positiva Verdadeira (eixo y) contra a Taxa Positiva Falsa (eixo x), pois você varia o limiar para atribuir observações a uma determinada classe. (Mais detalhes sobre as curvas ROC.)
E finalmente, para aqueles de vocês do mundo das estatísticas Bayesianas, aqui está um resumo rápido destes termos da Modelagem Preditiva Aplicada:
Em relação às estatísticas Bayesianas, a sensibilidade e especificidade são as probabilidades condicionais, a prevalência é a anterior, e os valores positivos/negativos previstos são as probabilidades posteriores.
Queres saber mais?
No meu novo vídeo de 35 minutos, Fazendo sentido a matriz de confusão, explico esses conceitos com mais profundidade e abordo tópicos mais avançados:
- Como calcular a precisão e a chamada para problemas multiclasse
- Como analisar uma matriz de confusão de 10 classes
- Como escolher a métrica de avaliação certa para o seu problema
- Por que a precisão é muitas vezes uma métrica enganosa
Deixe-me saber se você tem alguma dúvida!