Estes são processos de aprendizagem estocásticos com estrutura recorrente e são a base das técnicas de optimização precoce utilizadas na ANN. A Máquina Boltzmann foi inventada por Geoffrey Hinton e Terry Sejnowski em 1985. Mais clareza pode ser observada nas palavras de Hinton em Máquina Boltzmann.
“Uma característica surpreendente desta rede é que ela usa apenas informações disponíveis localmente. A mudança de peso depende apenas do comportamento das duas unidades que liga, embora a mudança otimize uma medida global” – Ackley, Hinton 1985.
Alguns pontos importantes sobre a Máquina Boltzmann –
-
Usam estrutura recorrente.
-
Consistem em neurônios estocásticos, que têm um dos dois estados possíveis, ou 1 ou 0.
-
Alguns dos neurónios neste estado são adaptáveis (estado livre) e alguns são fixados (estado congelado).
-
Se aplicarmos o recozimento simulado na rede discreta Hopfield, então ele se tornaria Máquina Boltzmann.
Objectivo da Máquina Boltzmann
O objectivo principal da Máquina Boltzmann é optimizar a solução de um problema. É o trabalho da Máquina Boltzmann para otimizar os pesos e a quantidade relacionada a esse problema em particular.
Arquitetura
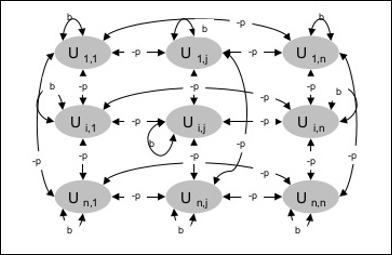
O diagrama seguinte mostra a arquitetura da Máquina Boltzmann. Está claro no diagrama, que é uma matriz bidimensional de unidades. Aqui, os pesos das interligações entre unidades são -p onde p > 0. Os pesos das interligações automáticas são dados por b onde b > 0.
Algoritmo de treino
Como sabemos que as máquinas Boltzmann têm pesos fixos, portanto não haverá algoritmo de treino, pois não precisamos de actualizar os pesos na rede. No entanto, para testar a rede temos que definir os pesos, bem como encontrar a função de consenso (CF).
Boltzmann máquina tem um conjunto de unidades Ui e Uj e tem conexões bi-direcionais sobre eles.
-
Consideramos o peso fixo, digamos wij.
-
wij ≠ 0 se Ui e Uj estiverem ligados.
-
Existe também uma simetria na interligação ponderada, i.e. wij = wji.
-
wii também existe, ou seja, haveria a auto-conexão entre unidades.
-
Para qualquer unidade Ui, seu estado ui seria ou 1 ou 0.
O objetivo principal da Máquina Boltzmann é maximizar a Função Consenso (CF) que pode ser dada pela seguinte relação
$CF\:==$CF\:{i}sum de exibição_{i}limites \w_{j}u_{i}u_{j}$$
Agora, quando o estado muda de 1 para 0 ou de 0 para 1, então a mudança de consenso pode ser dada pela seguinte relação –
$$$Delta CF=\(1):(1\:-:2u_{i})(w_{ij}:+:\i}displaystyle_{jneq i} u_{i} w_{ij})$$
Aqui ui é o estado actual de Ui.
A variação no coeficiente (1 – 2ui) é dada pela seguinte relação –
$$(1\:-:2u_{i}){i}:=:{casos}+1, & U_{i}:is:atualmente:fora de 1, & U_{i}:is:actualmente:on end{cases}$$
Geralmente, a unidade Ui não muda o seu estado, mas se mudar, então a informação estaria a residir local para a unidade. Com essa mudança, haveria também um aumento no consenso da rede.
Probabilidade da rede aceitar a mudança no estado da unidade é dada pela seguinte relação –
$AF(i,T)\:=$$Frac{1}{1\:+\:exp}$$
Aqui, T é o parâmetro de controle. Ele diminuirá conforme o CF atingir o valor máximo.
Algoritmo de teste
Passo 1 – Inicialize o seguinte para iniciar o treinamento –
- Pesos representando a restrição do problema
- Parâmetro de controle T
Passo 2 – Continue os passos 3-8, quando a condição de parada não for verdadeira.
Passo 3 – Executar os passos 4-7.
Passo 4 – Assumir que um dos estados mudou o peso e escolher o inteiro I, J como valores aleatórios entre 1 e n.
Passo 5 – Calcule a mudança de consenso da seguinte forma –
$$$\Delta CF\:=\:(1\:-:2u_{i})(w_{ij}:+\i}:\Limites do som do jogo_{jneq i} u_{i} w_{ij})$$
Passo 6 – Calcular a probabilidade de esta rede aceitar a mudança de estado
$AF(i,T){\i}(i,T){\i}
Caso II – se R ≥ AF, rejeite a alteração.
Aqui, R é o número aleatório entre 0 e 1.
Passo 8 – Reduza o parâmetro de controle (temperatura) da seguinte forma –
T(novo) = 0.95T(antigo)
Passo 9 – Teste para as condições de paragem que podem ser as seguintes –
- Temperatura atinge um valor especificado
- Não há alteração de estado para um número especificado de iterações