Objectivo de Aprendizagem
1. Converter de uma unidade para outra unidade do mesmo tipo.
Na seção 2.2 “Expressing Units”, mostramos alguns exemplos de como substituir unidades iniciais por outras unidades do mesmo tipo para obter um valor numérico que seja mais fácil de compreender. Nesta seção, formalizaremos o processo.
Considerar um exemplo simples: quantos pés existem em 4 jardas? A maioria das pessoas responderá quase automaticamente que existem 12 pés em 4 jardas. Como você fez essa determinação? Bem, se há 3 pés em 1 jarda e há 4 jardas, então há 4 × 3 = 12 pés em 4 jardas.
Isso é correto, é claro, mas é informal. Formalizemo-lo de uma forma que possa ser aplicada de uma forma mais geral. Sabemos que 1 jarda (yd) é igual a 3 pés (ft):
1 yd = 3 ft
Em matemática, esta expressão é chamada de igualdade. As regras da álgebra dizem que você pode mudar (isto é, multiplicar ou dividir ou adicionar ou subtrair) a igualdade (desde que você não divida por zero) e a nova expressão ainda será uma igualdade. Por exemplo, se dividirmos ambos os lados por 2, obtemos
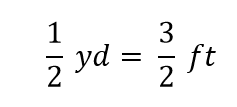
Vemos que meio metro é igual a 3/2, ou um metro e meio, pés – algo que também sabemos ser verdade, portanto a equação acima ainda é uma igualdade. Voltando à igualdade original, suponhamos que dividimos ambos os lados da equação por 1 metro (número e unidade):
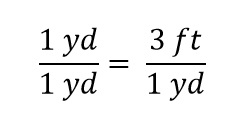
A expressão ainda é uma igualdade, pelas regras da álgebra. A fração esquerda é igual a 1. Ela tem a mesma quantidade no numerador e no denominador, portanto deve ser igual a 1. As quantidades no numerador e denominador cancelam, tanto o número como a unidade:
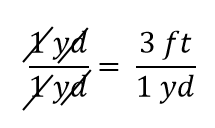
Quando tudo cancela numa fração, a fração se reduz a 1:
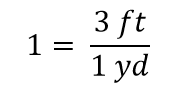
Temos uma expressão, 3 ft1 yd, que é igual a 1. Esta é uma forma estranha de escrever 1, mas faz sentido: 3 pés é igual a 1 yd, portanto as quantidades no numerador e denominador são a mesma quantidade, apenas expressas com unidades diferentes. A expressão 3 ft1 yd é chamada de fator de conversão, e é usada para mudar formalmente a unidade de uma quantidade para outra unidade. (O processo de conversão de unidades de uma forma tão formal é às vezes chamado de análise dimensional ou o método da etiqueta do fator)
Para ver como isso acontece, vamos começar com a quantidade original:
4 yd
Agora vamos multiplicar essa quantidade por 1. Quando você multiplica qualquer coisa por 1, você não muda o valor da quantidade. Ao invés de multiplicar por apenas 1, vamos escrever 1 como 3 ft1 yd:
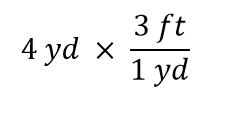
O termo 4 yd pode ser pensado como 4 yd/1; isto é, pode ser pensado como uma fração com 1 no denominador. Estamos essencialmente multiplicando as frações. Se a mesma coisa aparece no numerador e denominador de uma fração, elas se cancelam. Neste caso, o que cancela é a unidade quintal:
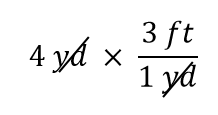
É tudo o que podemos cancelar. Agora, multiplique e divida todos os números para obter a resposta final: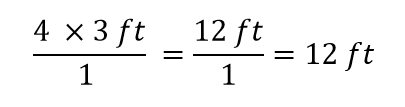
Again, obtemos uma resposta de 12 ft, tal como fizemos originalmente. Mas neste caso, usamos um procedimento mais formal que é aplicável a uma variedade de problemas.
Quantos milímetros são em 14,66 m? Para responder a isso, precisamos construir um fator de conversão entre milímetros e metros e aplicá-lo corretamente à quantidade original. Começamos com a definição de um milímetro, que é
1 mm = 1/1.000 m
O 1/1.000 é o que significa o prefixo milli-. A maioria das pessoas está mais confortável trabalhando sem frações, então vamos reescrever esta equação trazendo o 1.000 para o numerador do outro lado da equação:
1.000 mm = 1 m
Agora construímos um fator de conversão, dividindo uma quantidade em ambos os lados. Mas agora surge uma questão: por qual quantidade dividimos? Acontece que temos duas escolhas, e as duas escolhas nos darão diferentes fatores de conversão, ambos iguais a 1:
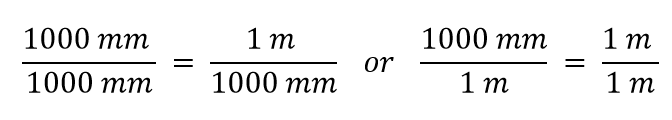
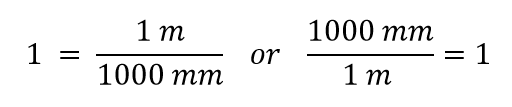
Que fator de conversão usamos? A resposta é baseada em que unidade você quer se livrar em sua quantidade inicial. A unidade original da nossa quantidade é o metro, que queremos converter em milímetros. Como a unidade original é assumida como estando no numerador, para nos livrarmos dela, queremos a unidade do contador no denominador; então eles irão cancelar. Portanto, vamos usar o segundo fator de conversão. Cancelando unidades e realizando a matemática, obtemos
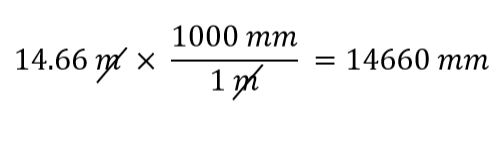
Nota como m cancela, deixando mm, que é a unidade de interesse.
A capacidade de construir e aplicar fatores de conversão adequados é uma técnica matemática muito poderosa em química. Você precisa dominar esta técnica para ter sucesso neste e em futuros cursos.
Exemplo 7
- Converter 35,9 kL para litros.
- Converter 555 nm para metros.
Solução
-
Utilizaremos o fato de que 1 kL = 1.000 L. Dos dois fatores de conversão que podem ser definidos, o que funcionará é 1.000 L/1 kL. Aplicando este fator de conversão, obteremos
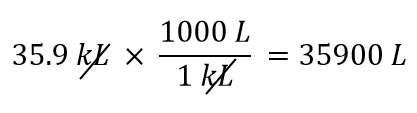
-
Usaremos o fato de que 1 nm = 1/1.000.000.000.000 m, que reescreveremos como 1.000.000.000 nm = 1 m, ou 109 nm = 1 m. Dos dois fatores de conversão possíveis, o apropriado tem a unidade nm no denominador: 1 m/109 nm. Aplicando este fator de conversão, obtemos
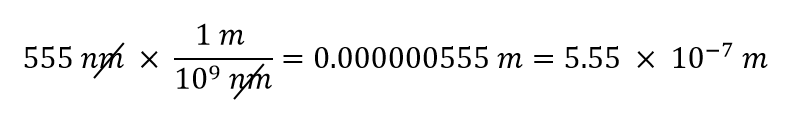
No passo final, expressamos a resposta em notação científica.
Test Yourself
- Convert 67.08 μL a litros.
- Convertido 56,8 m a quilómetros.
Respostas
- 6,708 × 10-5 L
- 5,68 × 10-2 km
E se tivermos uma unidade derivada que seja o produto de mais do que uma unidade, como por exemplo m2? Suponhamos que queremos converter metros quadrados em centímetros quadrados? A chave é lembrar que m2 significa m × m, o que significa que temos duas unidades de metro na nossa unidade derivada. Isso significa que temos de incluir dois factores de conversão, um para cada unidade. Por exemplo, para converter 17,6 m2 para centímetros quadrados, realizamos a conversão da seguinte forma:
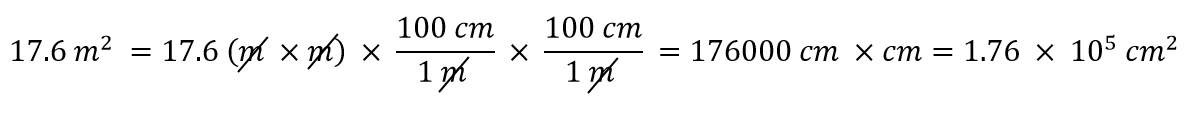
Exemplo 8
Quantos centímetros cúbicos estão em 0.883 m3?
Solução
Com um expoente de 3, temos três unidades de comprimento, portanto, por extensão, precisamos usar três fatores de conversão entre metros e centímetros. Assim, temos
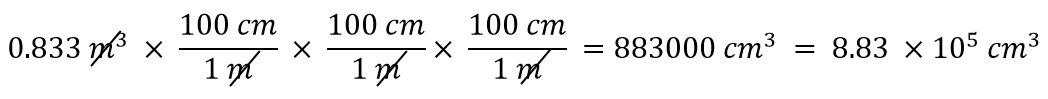
Você deve demonstrar a si mesmo que as unidades de três metros cancelam de fato.
Test Yourself
Quantos milímetros cúbicos estão presentes em 0,0923 m3?
Resposta
9,23 × 107 mm3
Suponha que a unidade que pretende converter está no denominador de uma unidade derivada; o que então? Então, no fator de conversão, a unidade que você quer remover deve estar no numerador. Isto irá cancelar com a unidade original no denominador e introduzir uma nova unidade no denominador. O exemplo seguinte ilustra esta situação.
Exemplo 9
Converter 88,4 m/min para metros/segundo.
Solução
Queremos mudar a unidade no denominador de minutos para segundos. Como há 60 segundos em 1 minuto (60 s = 1 min), construímos um fator de conversão para que a unidade que queremos remover, minutos, esteja no numerador: 1 min/60 s. Aplicar e executar a matemática:
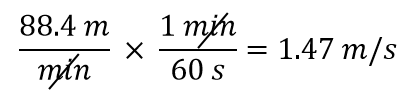
Notificar como o 88,4 vai automaticamente no numerador. Isso porque qualquer número pode ser pensado como estando no numerador de uma fração dividida por 1,
Test Yourself
Converter 0,203 m/min para metros/segundo.
Resposta
0.00338 m/s ou 3,38 × 10-3 m/s
Figure 2,8 Quão rápido é rápido?

Fonte: “Caracol da videira” de Jürgen Schoneris licenciado sob a licença Creative Commons Attribution-Share Alike 3.0 Unported License.