Sistema linear sub-determinado
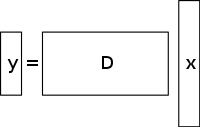
Um sistema sub-determinado de equações lineares tem mais incógnitas do que equações e geralmente tem um número infinito de soluções. A figura abaixo mostra tal sistema de equações y = D x {\\i1}mathbf {y} =D\ihbf {x} }
onde queremos encontrar uma solução para o x estilo de jogo }

.
Para escolher uma solução para tal sistema, deve-se impor restrições ou condições extras (como suavidade), conforme apropriado. No sensoriamento comprimido, adiciona-se a restrição de sparsity, permitindo apenas soluções que tenham um pequeno número de coeficientes não nulos. Nem todos os sistemas de equações lineares sub-determinados têm uma solução esparsa. No entanto, se existe uma solução esparsa única para o sistema sub-determinado, então a estrutura de sensoriamento comprimido permite a recuperação dessa solução.
Método de solução / reconstrução

A detecção comprimida aproveita a redundância em muitos sinais interessantes – eles não são ruído puro. Em particular, muitos sinais são esparsos, ou seja, contêm muitos coeficientes próximos ou iguais a zero, quando representados em algum domínio. Esta é a mesma percepção usada em muitas formas de compressão com perdas.
O sensoriamento comprimido normalmente começa com a tomada de uma combinação linear ponderada de amostras também chamada medições compressivas em uma base diferente da base na qual o sinal é conhecido por ser esparso. Os resultados encontrados por Emmanuel Candès, Justin Romberg, Terence Tao e David Donoho, mostraram que o número destas medições compressivas pode ser pequeno e ainda conter quase toda a informação útil. Portanto, a tarefa de converter a imagem de volta ao domínio pretendido envolve resolver uma equação matricial sub-determinada, uma vez que o número de medidas compressivas tomadas é menor do que o número de pixels na imagem completa. No entanto, adicionar a restrição de que o sinal inicial é esparso permite resolver este sistema sub-determinado de equações lineares.
A solução menos-quadrada para tais problemas é minimizar o L 2 {\displaystyle L^{2}}}.

norma-isto é, minimizar a quantidade de energia no sistema. Isto é geralmente simples matematicamente (envolvendo apenas uma multiplicação matricial pelo pseudo-inverso da base amostrada em). No entanto, isto leva a maus resultados para muitas aplicações práticas, para as quais os coeficientes desconhecidos têm energia não nula.
Para impor a restrição de sparsity quando se resolve para o sistema sub-determinado de equações lineares, pode-se minimizar o número de componentes não zero da solução. A função que conta o número de componentes não zero de um vetor foi chamada de L 0 ^{\i1}{0}}.

“norma” de David Donoho.
Candès et al. provaram que para muitos problemas é provável que o L 1 ^{\\i1}

norma é equivalente à L 0 ^{0}}{0}

norma, em sentido técnico: Este resultado de equivalência permite resolver o L 1 ^{\\i1}{\i1}

problema, que é mais fácil do que o L 0 ^{0}}{0}

problem. Encontrar o candidato com o menor L 1 ^{{1}{1}displaystyle L^{1}}

norma pode ser expressa com relativa facilidade como um programa linear, para o qual já existem métodos de solução eficientes. Quando as medições podem conter uma quantidade finita de ruído, a denoising de base é preferível à programação linear, uma vez que preserva a esparsidade em face do ruído e pode ser resolvida mais rapidamente do que um programa linear exato.
Construção de CS baseada na variação total
Motivação e aplicações
Regularização de TV
Variação total pode ser vista como uma função não negativa de valor real definida no espaço de funções de valor real (para o caso de funções de uma variável) ou no espaço de funções integráveis (para o caso de funções de várias variáveis). Para sinais, especialmente, a variação total refere-se à integral do gradiente absoluto do sinal. Na reconstrução de sinal e imagem, ela é aplicada como regularização da variação total onde o princípio subjacente é que sinais com detalhes excessivos têm alta variação total e que a remoção destes detalhes, embora retendo informações importantes como bordas, reduziria a variação total do sinal e tornaria o sinal sujeito mais próximo do sinal original no problema.
Para o propósito de reconstrução de sinal e imagem, l 1 {\displaystyle l1}

são utilizados modelos de minimização. Outras abordagens também incluem os mínimos quadrados, como já foi discutido anteriormente neste artigo. Estes métodos são extremamente lentos e devolvem uma reconstrução não tão perfeita do sinal. Os modelos atuais de regularização CS tentam resolver este problema incorporando os priores sparsity da imagem original, um dos quais é a variação total (TV). As abordagens convencionais de TV são projetadas para dar soluções constantes por peça. Algumas delas incluem (como discutido adiante) – a minimização limitada l1 que usa um esquema iterativo. Este método, embora rápido, leva subsequentemente a um excesso de suavização de bordas resultando em bordas de imagem embaçadas. Métodos de TV com re-peso iterativo foram implementados para reduzir a influência de grande gradiente de magnitudes de valor nas imagens. Isto tem sido usado na reconstrução tomográfica computorizada (TC) como um método conhecido como variação total de preservação de bordas. Entretanto, como as magnitudes de gradiente são usadas para estimar os pesos relativos de penalidade entre os termos de fidelidade dos dados e de regularização, este método não é robusto a ruídos e artefatos e suficientemente preciso para a reconstrução da imagem/sinal de CS e, portanto, não consegue preservar estruturas menores.
Progresso recente neste problema envolve o uso de um refinamento de TV iterativamente direcional para a reconstrução de CS. Este método teria 2 estágios: o primeiro estágio estimaria e refinaria o campo de orientação inicial – que é definido como uma estimativa inicial ruidosa, através da detecção de borda, da imagem dada. Na segunda etapa, o modelo de reconstrução do CS é apresentado utilizando o regularizador direcional de TV. Mais detalhes sobre estas abordagens baseadas em TV – minimização l1 iterativamente reponderada, TV com preservação de borda e modelo iterativo usando campo de orientação direcional e TV – são fornecidos abaixo.
Abordagens existentes
Iterativamente reponderada l 1 {\displaystyle l_{1}}


minimização

Nos modelos de reconstrução de CS usando l_{1}{\displaystyle l_{1}}displaystyle l_{1}

minimização, os coeficientes maiores são penalizados fortemente no l 1 {\\i1}

norm. Foi proposto ter uma formulação ponderada de l 1 {\\i1}{\i1}{\i1}.

minimização destinada a penalizar mais democraticamente os coeficientes não nulos. Um algoritmo iterativo é usado para a construção dos pesos apropriados. Cada iteração requer a resolução de um l 1 {\displaystyle l_{1}}}.

problema de minimização ao encontrar o mínimo local de uma função de penalização côncava que mais se assemelha ao l 0 {\\i1}{0}}

norm. Um parâmetro adicional, normalmente para evitar transições bruscas na curva da função penalidade, é introduzido na equação iterativa para garantir a estabilidade e para que uma estimativa zero em uma iteração não leve necessariamente a uma estimativa zero na próxima iteração. O método envolve essencialmente o uso da solução atual para calcular os pesos a serem usados na próxima iteração.
Vantagens e desvantagens
As iterações precoces podem encontrar estimativas de amostra imprecisas, no entanto este método irá diminuir a amostragem destas numa fase posterior para dar mais peso às estimativas de sinal menor que não seja zero. Uma das desvantagens é a necessidade de definir um ponto de partida válido, pois um mínimo global pode não ser obtido toda vez devido à concavidade da função. Outra desvantagem é que este método tende a penalizar uniformemente o gradiente da imagem, independentemente das estruturas de imagem subjacentes. Isto causa um excesso de suavização das bordas, especialmente as de regiões de baixo contraste, levando subsequentemente à perda de informação de baixo contraste. As vantagens deste método incluem: redução da taxa de amostragem para sinais esparsos; reconstrução da imagem ao mesmo tempo em que é robusta à remoção de ruído e outros artefatos; e uso de muito poucas iterações. Isto também pode ajudar na recuperação de imagens com gradientes esparsos.
Na figura abaixo, P1 refere-se ao primeiro passo do processo de reconstrução iterativa, da matriz de projeção P da geometria do feixe de ventoinha, que é restringida pelo termo de fidelidade dos dados. Isto pode conter ruídos e artefatos, uma vez que não é feita qualquer regularização. A minimização da P1 é resolvida pelo método dos mínimos quadrados de gradiente conjugado. P2 refere-se à segunda etapa do processo de reconstrução iterativa onde se utiliza o termo de regularização de variação total com preservação de borda para remover ruído e artefatos, melhorando assim a qualidade da imagem/sinal reconstruído. A minimização do P2 é feita através de um método simples de descida por gradiente. A convergência é determinada testando, após cada iteração, a positividade da imagem, verificando se f k – 1 = 0 {\displaystyle f^{k-1}=0}.

para a caixa quando f k – 1 < 0 {\f^{k-1}<0}

(Note que f {\f}displaystyle f}

refere-se aos diferentes coeficientes de atenuação linear de raios X em diferentes voxels da imagem do paciente).
Variação total com preservação de borda (TV) baseada no sensoriamento comprimido

Este é um algoritmo iterativo de reconstrução de TC com regularização de TV com preservação de borda para reconstruir imagens de TC a partir de dados altamente subamostragem obtidos em TC de baixa dose através de níveis de corrente baixos (milliampere). A fim de reduzir a dose de imagem, uma das abordagens utilizadas é reduzir o número de projecções de raios X adquiridas pelos detectores do scanner. No entanto, estes dados insuficientes de projeção que são usados para reconstruir a imagem da tomografia computadorizada podem causar artefatos de estrias. Além disso, a utilização destas projecções insuficientes em algoritmos de TV padrão acaba por tornar o problema sub-determinado, levando assim a infinitas soluções possíveis. Neste método, uma função adicional ponderada por penalidades é atribuída à norma original da TV. Isto permite a detecção mais fácil de descontinuidades de intensidade nítidas nas imagens e, assim, adaptar o peso para armazenar a informação de borda recuperada durante o processo de reconstrução do sinal/imagem. O parâmetro σ {\i1}displaystyle {\i1}sigma

controla a quantidade de suavização aplicada aos pixels nas bordas para diferenciá-los dos pixels sem bordas. O valor de σ {\displaystyle \sigma {\displaystyle \sigma }

é alterado adaptivamente com base nos valores do histograma da magnitude de gradiente, de modo a que uma certa percentagem de pixels tenha valores de gradiente maiores do que σ {\sigma {\sigma }

. O termo de variação total de preservação de borda, assim, torna-se mais esparso e isso acelera a implementação. Um processo de iteração em duas etapas conhecido como algoritmo de divisão para frente e para trás é usado. O problema de otimização é dividido em dois sub-problemas que são então resolvidos com o método conjugado de mínimos quadrados de gradiente e o método simples de descida de gradiente respectivamente. O método é interrompido quando a convergência desejada é alcançada ou se o número máximo de iterações é alcançado.
Vantagens e desvantagens
Algumas das desvantagens deste método são a ausência de estruturas menores na imagem reconstruída e a degradação da resolução da imagem. Esta margem preservando o algoritmo de TV, no entanto, requer menos iterações do que o algoritmo convencional de TV. Analisando os perfis de intensidade horizontal e vertical das imagens reconstruídas, pode-se observar que há saltos nítidos em pontos de borda e flutuações insignificantes e menores em pontos sem borda. Assim, este método leva a um erro relativo baixo e a uma correlação mais alta em comparação com o método de TV. Ele também suprime e remove eficazmente qualquer forma de ruído de imagem e artefatos de imagem, como estrias.
Modelo iterativo usando um campo de orientação direcional e variação total direcional
Para evitar o excesso de suavização de bordas e detalhes de textura e para obter uma imagem de CS reconstruída que seja precisa e robusta a ruídos e artefatos, este método é usado. Primeiro, uma estimativa inicial do campo de orientação no sentido do ruído da imagem I {\displaystyle I}.

, d ^ ^displaystyle ^{\an8}}

, é obtido. Este campo de orientação ruidoso é definido para que possa ser refinado numa fase posterior para reduzir as influências do ruído na estimativa do campo de orientação. Uma estimativa de campo de orientação grosseira é então introduzida com base no tensor de estrutura que é formulado como: J ρ ( ∇ I σ ) = G ρ ∗ ( ∇ I σ ⊗ ∇ I σ ) = ( J 11 J 12 J 12 J 22 ) {\i1}(\i1}nabla I_{\i}{\i1}(\i1}sigma G_Rho**(nabla I_sigma**(nabla I_sigma**) ={\i1}(G_{\i1}}begin{\i1}J_{11}&J_{12}}J_{12}&J_{22}{\i}end{\i1} Aqui, J ρ {\\i1}displaystyle J_{\i1}{\i1}rho

refere-se ao tensor de estrutura relacionado com o ponto de pixel da imagem (i,j) com desvio padrão ρ {\rho {\rho }

. G estilo G

refere-se ao kernel gaussiano ( 0 , ρ 2 ) {\\i1} {\i1}displaystyle (0,\i}rho ^{\i})}

com desvio padrão ρ {\rho ^{\rho ^{\rho ^}

. σ {\i1}displaystyle {\i}sigma

refere-se ao parâmetro definido manualmente para a imagem I {\displaystyle I}

abaixo do qual a detecção de bordas é insensível ao ruído. ∇ I σ {\i1}displaystyle {\i1}nabla I_sigma {\i}}

refere-se ao gradiente da imagem I {\displaystyle I}

e ( ∇ I σ ⊗ ∇ I σ ) {\i1}displaystyle (nabla I_{\i1}otimes {\i}nabla I_{\i}

refere-se ao produto tensor obtido pelo uso deste gradiente.
O tensor de estrutura obtido está envolvido por um grão G {\\i1}displaystyle G}

para melhorar a precisão da estimativa de orientação com σ {\i1}displaystyle {\i}sigma

sendo ajustado para valores altos para contabilizar os níveis de ruído desconhecidos. Para cada pixel (i,j) da imagem, o tensor estrutural J é uma matriz simétrica e semi-definida positiva. Girando todos os pixels da imagem com G {\displaystyle G}

, dá vectores próprios orthonormais ω e υ do J {\i1}displaystyle J

matriz. ω aponta na direção da orientação dominante tendo o maior contraste e υ aponta na direção da orientação da estrutura tendo o menor contraste. A estimativa inicial grosseira do campo de orientação d ^ ^ ^ estilo de exibição ^ que ^ ^

é definido como d ^ ^ ^ estilo de exibição ^{\a}}

= υ. Esta estimativa é precisa em bordas fortes. No entanto, em bordas fracas ou em regiões com ruído, sua confiabilidade diminui.
Para superar este inconveniente, um modelo de orientação refinada é definido no qual o termo de dados reduz o efeito do ruído e melhora a precisão, enquanto o segundo termo de penalidade com a norma L2 é um termo de fidelidade que garante a precisão da estimativa inicial grosseira.
Este campo de orientação é introduzido no modelo de otimização da variação total direcional para reconstrução de CS através da equação: m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\i1}displaystyle min_{\i} {\i1}lVert {\i}lVert {\i}nabla {\i}mathrm {\i} {\i1}{\i1}rVert _{\i}+{\i1}frac {\i}lambda {\i} {\i1}lVert Y- Phi {\i}mathrm {\i} {\i}rVert _\i}^{\i}

. X-Estilo de exibição X-

é o sinal objectivo que precisa de ser recuperado. Y é o vector de medição correspondente, d é o campo de orientação refinado iterativo e Φ {\i1}displaystyle {\i}

é a matriz de medição CS. Este método passa por algumas iterações que acabam por levar à convergência. d ^ ^ Estilo de visualização ^

é a estimativa aproximada do campo de orientação da imagem reconstruída X k – 1 ^{k-1}}

da iteração anterior (para verificar a convergência e o desempenho óptico subsequente, é utilizada a iteração anterior). Para os dois campos vetoriais representados por X {\mathrm {X} }

e d {\displaystyle d}

, X ∙ d {\i1}displaystyle {\i}mathrm {X} {\i}bullet d}

refere-se à multiplicação dos respectivos elementos vectoriais horizontais e verticais do X\mathrm {X}

e d {\displaystyle d}

seguido da sua posterior adição. Estas equações são reduzidas a uma série de problemas de minimização convexa que são então resolvidos com uma combinação de métodos de divisão variável e métodos de Lagrangian (solver rápido baseado em FFT com uma solução de forma fechada). Ele (Lagrangiano Aumentado) é considerado equivalente à iteração Bregman dividida, o que garante a convergência deste método. O campo de orientação, d é definido como sendo igual a ( d h , d v ) {\displaystyle (d_{h},d_{v})}

, onde d h , d v {\displaystyle d_{h},d_{v}}}

definir as estimativas horizontais e verticais de d {\i1}displaystyle d}

.

Método Lagrangiano Aumentado para o campo de orientação, m i n X ‖ ∇ X ∙ d ‖ 1 + λ 2 ‖ Y – Φ X ‖ 2 2 {\i1}displaystyle min_{\i} {\i1}lVert {\i1}lVert {\i}nabla {\i}mathrm {\i} {\i1}rVert _{\i}+frac {\i}lambda {\i} {\i1}lVert Y- Phi {\i}mathrm {\i} {\i}rVert _\i}{\i}
 >
>, envolve inicializar d h , d v , H , V {\i1}displaystyle d_{h},d_{v},H,V}

e depois encontrar o minimizador aproximado de L 1 {\\i1}{\i1}

em relação a estas variáveis. Os multiplicadores Lagrangianos são então atualizados e o processo iterativo é interrompido quando a convergência é alcançada. Para o modelo de refinamento da variação total iterativa direcional, o método lagrangiano aumentado envolve inicializar X , P , Q , λ P , λ Q {\\i1}mathrm {X} ,P,Q,\i}lambda _{P},\i}lambda _{Q}}}

.
Aqui, H , V , P , Q {\\i1}displaystyle H,V,P,Q}

são variáveis recentemente introduzidas onde H {\i1}displaystyle H}

= ∇ d h {\i1}displaystyle {\i}nabla d_{\i}

, V {\displaystyle V}

= ∇ d v {\i1}displaystyle {\i}nabla d_{v}}

, P {\i1}displaystyle P}

= ∇ X {\i1}displaystyle {\i}nabla {\i}mathrm

, e Q {\i1}displaystyle Q

= P ∙ d {\i1}displaystyle P\i}bullet d

. λ H , λ V , λ P , λ Q {\i1}displaystyle {H},{\i}lambda _{V},{\i}lambda _{P},{\i}lambda _{Q}}
são os multiplicadores Lagrangianos para H,V,P , Q {\i1}displaystyle H,V,P,Q}

. Para cada iteração, o minimizador aproximado de L 2 {\\i1} é o estilo L_{\i}}

com respeito às variáveis ( X , P , Q {\i1}displaystyle {X} ,P,Q}

) é calculado. E como no modelo de refinamento de campo, os multiplicadores lagrangianos são atualizados e o processo iterativo é interrompido quando a convergência é alcançada.
Para o modelo de refinamento de campo de orientação, os multiplicadores lagrangianos são atualizados no processo iterativo da seguinte forma:
( λ H ) k = ( λ H ) k – 1 + γ H ( H k – ∇ ( d h ) k ) ^{\displaystyle (\lambda _{H})^{k}=(\lambda _{H})^{k-1}+\gamma _{H}(H^{k}-\nabla (d_{h})^{k})}

( λ V ) k = ( λ V ) k – 1 + γ V ( V k – ∇ ( d v ) k ) ^{k}=(\lambda _{V})^{k}=(\lambda _{V})^{k-1}+\gamma _{V}(V^{k}-{v}-nabla (d_{v})^{k}} }

Para o modelo iterativo de refinamento da variação total direcional, os multiplicadores Lagrangianos são atualizados da seguinte forma:
( λ P ) k = ( λ P ) k – 1 + γ P ( P k – ∇ ( X ) k ) {\i1} ^{k}=(\i}lambda _{P})^{k}=(\i1}+\i}gamma _{P}(P^{k}-{nabla (\i}- mathrm {X} )^{k})}

( λ Q ) k = ( λ Q ) k – 1 + γ Q ( Q k – P k ∙ d ) ^{\k}=(\lambda _{Q})^{k-1}+\gamma _{Q}(Q^{k}-P^{k}-P^{k}}}bullet d)}

Aqui, γ H , γ V , γ P , γ Q {\i1}displaystyle {H},{\i}gamma _{V},{\i}gamma _{P},{\i}gamma _{Q}}

são constantes positivas.
Vantagens e desvantagens
Baseado na relação sinal/ruído de pico (PSNR) e nas métricas do índice de similaridade estrutural (SSIM) e imagens da verdade do solo conhecidas para testar o desempenho, conclui-se que a variação total direcional iterativa tem um desempenho reconstruído melhor do que os métodos não iterativos na preservação das áreas de borda e textura. O modelo de refinamento do campo de orientação desempenha um papel importante nesta melhoria no desempenho, pois aumenta o número de pixels sem direção na área plana, enquanto melhora a consistência do campo de orientação nas regiões com bordas.