Barycentriska koordinater

av
Geometri > Koordinatgeometri >
Geometri > Plangeometri > Trianglar > Egenskaper för trianglar >

Barycentriska koordinater är triplar av tal (t_1,t_2,t_3) som motsvarar massor placerade vid hörnen av en referenstriangel DeltaA_1A_2A_3. Dessa massor bestämmer sedan en punkt P, som är den geometriska mittpunkten för de tre massorna och identifieras med koordinaterna (t_1,t_2,t_3). Triangelns hörn ges av (1,0,0), (0,1,0) och (0,0,1). Barycentriska koordinater upptäcktes av Möbius 1827 (Coxeter 1969, s. 217; Fauvel et al. 1993).

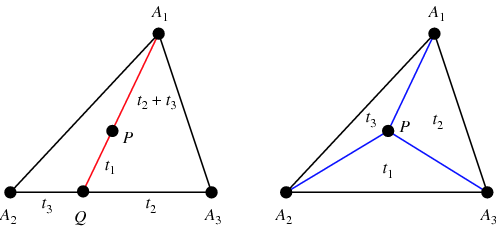
Barycentric

För att hitta de barycentriska koordinaterna för en godtycklig punkt P, hitta t_2 och t_3 från punkten Q i skärningspunkten mellan linjen A_1P och sidan A_2A_3, och bestäm sedan t_1 som den massa i A_1 som kommer att balansera en massa t_2+t_3 i Q, vilket gör P till mittpunkten (vänster figur). Vidare är areorna av trianglarna DeltaA_1A_2P, DeltaA_1A_3P och DeltaA_2A_3P proportionella mot de barycentriska koordinaterna t_3, t_2 och t_1 för P (höger figur; Coxeter 1969, s. 217).

Barycentriska koordinater är homogena, så

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

för mu!=0.

Barycentriska koordinater som normaliserats så att de blir de faktiska areorna av undertrianglarna kallas homogena barycentriska koordinater. Barycentriska koordinater normaliserade så att

t_1+t_2+t_3=1,
(2)

så att koordinaterna ger ytorna av subtrianglarna normaliserade med ytorna av den ursprungliga triangeln kallas för areal-koordinater (Coxeter 1969, s. 218). Barycentriska och arealkoordinater kan ge särskilt eleganta bevis för geometriska satser som Rouths sats, Cevas sats och Menelaus sats (Coxeter 1969, s. 219-221).

(Inte nödvändigtvis homogena) barycentriska koordinater för ett antal vanliga centra sammanfattas i följande tabell. I tabellen är a, b och c sidlängderna i triangeln och s är dess semiperimeter.

triangelns centrum barycentriska koordinater
omkretscentrum O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
Gergonnepunkt Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
Nagelpunkt Na (s-a,s-b,s-c)
ortocenter H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symmetripunkt K (a^2,b^2,c^2)
triangelcentroid G (1,1,1)

I barycentriska koordinater har en linje en linjär homogen ekvation. I synnerhet har linjen som förbinder punkterna (r_1,r_2,r_3) och (s_1,s_2,s_3) ekvationen

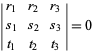|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 och 57; Coxeter 1969, s. 219; Bottema 1982). Om hörnen P_i i en triangel DeltaP_1P_2P_3 har barycentriska koordinater (x_i,y_i,z_i), så är triangelns area

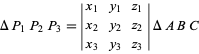DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Lämna en kommentar