Dessa är stokastiska inlärningsprocesser som har en återkommande struktur och ligger till grund för de tidiga optimeringstekniker som används i ANN. Boltzmann Machine uppfanns av Geoffrey Hinton och Terry Sejnowski 1985. Hintons ord om Boltzmann Machine är tydligare:
”En överraskande egenskap hos detta nätverk är att det endast använder lokalt tillgänglig information. Viktförändringen beror endast på beteendet hos de två enheter som den förbinder, även om förändringen optimerar ett globalt mått.” – Ackley, Hinton 1985.
Några viktiga punkter om Boltzmann Machine –
-
De använder sig av en återkommande struktur.
-
De består av stokastiska neuroner, som har ett av de två möjliga tillstånden, antingen 1 eller 0.
-
En del av neuronerna i detta är adaptiva (fritt tillstånd) och en del är klämda (fruset tillstånd).
-
Om vi tillämpar simulerad glödgning på ett diskret Hopfield-nätverk skulle det bli en Boltzmannmaskin.
Boltzmannmaskinens syfte
Boltzmannmaskinens huvudsyfte är att optimera lösningen på ett problem. Boltzmannmaskinens uppgift är att optimera de vikter och den kvantitet som är relaterade till det aktuella problemet.
Arkitektur
Följande diagram visar arkitekturen hos Boltzmannmaskinen. Det framgår tydligt av diagrammet att det är en tvådimensionell matris av enheter. Här är vikterna på sammankopplingar mellan enheterna -p där p > 0. Vikterna på självförbindelser ges av b där b > 0.
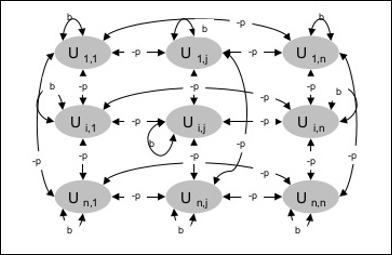
Träningsalgoritm
Som vi vet att Boltzmann-maskiner har fasta vikter, kommer det därför inte att finnas någon träningsalgoritm eftersom vi inte behöver uppdatera vikterna i nätverket. För att testa nätverket måste vi dock ställa in vikterna samt hitta konsensusfunktionen (CF).
Boltzmann-maskinen har en uppsättning enheter Ui och Uj och har dubbelriktade förbindelser på dem.
-
Vi betraktar den fasta vikten säg wij.
-
wij ≠ 0 om Ui och Uj är sammankopplade.
-
Det finns också en symmetri i den viktade sammankopplingen, dvs.d.v.s. wij = wji.
-
wii finns också, d.v.s. det skulle finnas självförbindelse mellan enheter.
-
För varje enhet Ui skulle dess tillstånd ui vara antingen 1 eller 0.
Boltzmannmaskinens huvudmål är att maximera konsensusfunktionen (CF) som kan ges av följande relation
$$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$$
Nu, när tillståndet ändras från antingen 1 till 0 eller från 0 till 1, kan förändringen i konsensus ges av följande relation –
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
Här är ui det aktuella tillståndet för Ui.
Variationen i koefficienten (1 – 2ui) ges av följande relation –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\\-1, & U_{i}\:is\:currently\:on\end{cases}$$$
Enheten Ui ändrar i allmänhet inte sitt tillstånd, men om den gör det skulle informationen vara lokal för enheten. I och med den förändringen skulle också nätverkets konsensus öka.
Nätverkets sannolikhet att acceptera en förändring av enhetens tillstånd ges av följande relation –
$$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$$
Här är T den styrande parametern. Den kommer att minska när CF når maximalt värde.
Testalgoritm
Steg 1 – Initialisera följande för att starta träningen –
- Vikter som representerar problemets begränsningar
- Kontrollparameter T
Steg 2 – Fortsätt steg 3-8, när stoppvillkoret inte är sant.
Steg 3 – Utför steg 4-7.
Steg 4 – Anta att ett av tillstånden har ändrat vikten och välj heltalet I, J som slumpmässiga värden mellan 1 och n.
Steg 5 – Beräkna förändringen i konsensus enligt följande –
$$\\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$$
Steg 6 – Beräkna sannolikheten för att detta nätverk skulle acceptera ändringen i tillståndet
$$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$$
Steg 7 – Acceptera eller förkasta denna förändring enligt följande –
Fall I – om R < AF, acceptera förändringen.
Fall II – om R ≥ AF, förkasta ändringen.
Här är R ett slumpmässigt tal mellan 0 och 1.
Steg 8 – Minska styrparametern (temperatur) enligt följande –
T(ny) = 0.95T(gammal)
Steg 9 – Testa för stoppvillkoren som kan vara följande –
- Temperaturen når ett specificerat värde
- Det sker ingen förändring av tillståndet under ett specificerat antal iterationer