Biografi

Brahmagupta (598-668 e.Kr.)
Den store indiske matematikern och astronomen Brahmagupta, som är född på 700-talet, skrev en del viktiga verk om både matematik och astronomi. Han kom från delstaten Rajasthan i nordvästra Indien (han kallas ofta Bhillamalacarya, läraren från Bhillamala) och blev senare chef för det astronomiska observatoriet i Ujjain i centrala Indien. De flesta av hans verk är komponerade på elliptisk vers, en vanlig metod inom indisk matematik vid den tiden, och har följaktligen något av en poetisk klang.
Det är troligt att Brahmaguptas verk, särskilt hans mest kända text, ”Brahmasphutasiddhanta”, togs med av den abbasidiska kalifen Al-Mansur på 700-talet till hans nygrundade lärdomscentrum i Bagdad vid Tigris’ stränder, och att de därmed utgjorde en viktig länk mellan indisk matematik och astronomi och det begynnande uppsvinget för vetenskap och matematik i den islamiska världen.
I sitt arbete om aritmetik förklarade Brahmagupta hur man hittar kubik och kubikrot av ett heltal och gav regler som underlättade beräkningen av kvadrater och kvadratrötter. Han gav också regler för att hantera fem typer av kombinationer av bråk. Han angav summan av kvadraterna av de första n naturliga talen som n(n + 1)(2n + 1)⁄ 6 och summan av kuberna av de första n naturliga talen som (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Behandla nollan som ett tal

Brahmaguptas regler för att hantera nollor och negativa tal
Brahmaguptas genialitet kom dock i hans behandling av begreppet (då relativt nytt) talet noll. Även om hans ”Brahmasphutasiddhanta” ofta också tillskrivs den indiske matematikern Bhaskara I från 700-talet, är den troligen den tidigaste kända texten där nollan behandlas som ett eget tal, snarare än som en platshållande siffra, vilket gjordes av babylonierna, eller som en symbol för brist på kvantitet, vilket gjordes av grekerna och romarna.
Brahmagupta fastställde de grundläggande matematiska reglerna för att hantera noll (1 + 0 = 1; 1 – 0 = 1; och 1 x 0 = 0), även om hans förståelse av division med noll var ofullständig (han trodde att 1 ÷ 0 = 0). Nästan 500 år senare, på 1100-talet, visade en annan indisk matematiker, Bhaskara II, att svaret borde vara oändlighet, inte noll (med motiveringen att 1 kan delas i ett oändligt antal bitar av storlek noll), ett svar som ansågs korrekt i århundraden. Denna logik förklarar dock inte varför 2 ÷ 0, 7 ÷ 0 osv. också borde vara noll – den moderna uppfattningen är att ett tal dividerat med noll faktiskt är ”odefinierat” (dvs. det har ingen mening).
Brahmaguptas syn på tal som abstrakta entiteter, i stället för att bara vara till för att räkna och mäta, gjorde det möjligt för honom att göra ännu ett enormt konceptuellt språng, som skulle få djupgående konsekvenser för den framtida matematiken. Tidigare ansågs till exempel summan 3 – 4 vara antingen meningslös eller i bästa fall bara noll. Brahmagupta insåg emellertid att det kunde finnas något sådant som ett negativt tal, vilket han kallade ”skuld” i motsats till ”egenskap”. Han redogjorde för reglerna för hur man hanterar negativa tal (t.ex. att ett negativt tal gånger ett negativt tal är ett positivt tal, ett negativt tal gånger ett positivt tal är ett negativt tal osv.)
Fortfarande påpekade han att kvadratiska ekvationer (av typen x2 + 2 = 11, t.ex.) i teorin skulle kunna ha två möjliga lösningar, varav den ena skulle kunna vara negativ, eftersom 32 = 9 och -32 = 9. Förutom sitt arbete med lösningar på allmänna linjära ekvationer och kvadratiska ekvationer gick Brahmagupta ännu längre genom att överväga system av simultana ekvationer (uppsättning ekvationer som innehåller flera variabler) och lösa kvadratiska ekvationer med två okända, något som inte ens övervägdes i västvärlden förrän tusen år senare, när Fermat tog upp liknande problem år 1657.
Brahmaguptas sats om cykliska fyrhörningar
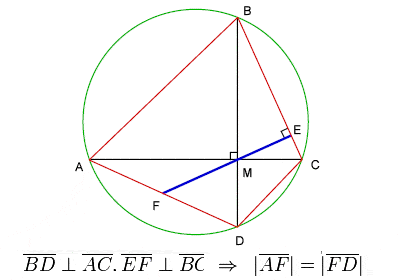
Brahmaguptas sats om cykliska fyrhörningar
Brahmagupta försökte till och med skriva ner dessa ganska abstrakta begrepp, genom att använda initialer till färgernas namn för att representera okända i sina ekvationer, en av de tidigaste antydningarna till det som vi nu känner till som algebra.
Brahmagupta ägnade en betydande del av sitt arbete åt geometri och trigonometri. Han fastställde √10 (3,162277) som en bra praktisk approximation av π (3,141593) och gav en formel, som nu är känd som Brahmaguptas formel, för arean av en cyklisk fyrhörning, samt en berömd sats om diagonalerna i en cyklisk fyrhörning, som vanligtvis kallas Brahmaguptas sats.
| << Tillbaka till indisk matematik |
Framåt till Madhava >> |