En cellulär automat är en samling ”färgade” celler på ett rutnät med bestämd form som utvecklas genom ett antal diskreta tidssteg i enlighet med en uppsättning regler baserade på tillstånden hos angränsande celler. Reglerna tillämpas sedan iterativt i så många tidssteg som önskas. von Neumann var en av de första som övervägde en sådan modell och införlivade en cellulär modell i sin ”universalkonstruktör”. Cellulära automater studerades i början av 1950-talet som en möjlig modell för biologiska system (Wolfram 2002, s. 48). Omfattande studier av cellulära automater har utförts av S. Wolfram med början på 1980-talet, och Wolframs grundläggande forskning på området kulminerade i publiceringen av hans bok A New Kind of Science (Wolfram 2002), där Wolfram presenterar en gigantisk samling resultat om automater, bland vilka finns ett antal banbrytande nya upptäckter.
I avsnittet ”Bettor or Worse” (2006) i säsong 2 av TV-kriminaldramat NUMB3RS nämns endimensionella cellulära automater.
Cellulära automater finns i en mängd olika former och varianter. En av de mest grundläggande egenskaperna hos en cellulär automat är den typ av rutnät som den beräknas på. Det enklaste sådana ”rutnätet” är en endimensionell linje. I två dimensioner kan man överväga kvadratiska, triangulära och hexagonala rutnät. Cellulära automater kan också konstrueras på kartesiska rutnät i ett godtyckligt antal dimensioner, där det 
-dimensionella heltalsgitteret 
är det vanligaste valet. Cellulära automater på ett 
-dimensionellt heltalsgitter implementeras i Wolfram Language som CellularAutomaton.
Antalet färger (eller distinkta tillstånd) 
som en cellulär automat kan anta måste också anges. Detta antal är vanligtvis ett heltal, där 
(binärt) är det enklaste valet. För en binär automat brukar färg 0 kallas ”vit” och färg 1 brukar kallas ”svart”. Cellulära automater som har ett kontinuerligt intervall av möjliga värden kan dock också övervägas.
Förutom det rutnät som en cellulär automat lever på och de färger som dess celler kan anta, måste också det grannskap över vilket cellerna påverkar varandra specificeras. Det enklaste valet är ”närmaste grannar”, där endast celler som är direkt angränsande till en viss cell kan påverkas vid varje tidssteg. Två vanliga grannskap i fallet med en tvådimensionell cellulär automat på ett kvadratiskt rutnät är det så kallade Moores grannskap (ett kvadratiskt grannskap) och von Neumanns grannskap (ett diamantformat grannskap).
Den enklaste typen av cellulär automat är en binär, närmaste grannar, endimensionell automat. Sådana automater kallades ”elementära cellulära automater” av S. Wolfram, som utförligt har studerat deras fantastiska egenskaper (Wolfram 1983; 2002, s. 57). Det finns 256 sådana automater, och var och en av dem kan indexeras med ett unikt binärt tal vars decimalrepresentation är känd som ”regeln” för den särskilda automaten. En illustration av regel 30 visas ovan tillsammans med den utveckling den ger upphov till efter 15 steg med utgångspunkt i en enda svart cell.
En något mer komplicerad klass av cellulära automater är de närmast närliggande, 
-färgade, endimensionella totalistiska cellulära automaterna. I sådana automater är det genomsnittet av intilliggande celler som bestämmer utvecklingen, och de enklaste icke-triviala exemplen har 
färger. För dessa automater kan den uppsättning regler som beskriver beteendet kodas som ett 
-siffrigt 
-ary-nummer som kallas ”kod”. Reglerna och de 300 stegen i den ternära (
) koden 912-automaten illustreras ovan.
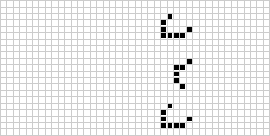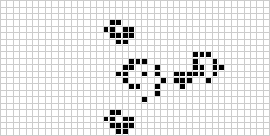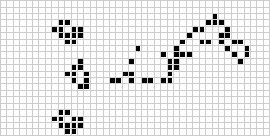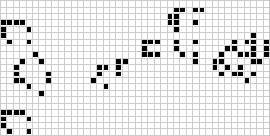
I två dimensioner är den mest kända cellulära automaten Conways livsspel, som upptäcktes av J. H. Conway 1970 och som populariserades i Martin Gardners kolumner i Scientific American. Livets spel är en binär (
) totalistisk cellulär automat med ett Mooreskt grannskap i intervallet 
. Även om beräkningen av på varandra följande generationer av livets spel ursprungligen gjordes för hand, kom datorrevolutionen snart och möjliggjorde att mer omfattande mönster kunde studeras och spridas. En animation av en konstruktion av game of life känd som puffer train illustreras ovan.
WireWorld är en annan vanlig tvådimensionell cellularautomat.
Teorin om cellulära automater är oerhört rik, med enkla regler och strukturer som kan ge upphov till ett stort antal oväntade beteenden. Det finns till exempel universella cellulära automater som kan simulera beteendet hos alla andra cellulära automater eller Turingmaskiner. Gacs (2001) har till och med bevisat att det finns feltoleranta universella cellulära automater vars förmåga att simulera andra cellulära automater inte hindras av slumpmässiga störningar, förutsatt att dessa störningar är tillräckligt fåtaliga.