En förvirringsmatris är en tabell som ofta används för att beskriva resultatet av en klassificeringsmodell (eller ”klassificerare”) på en uppsättning testdata för vilka de sanna värdena är kända. Själva förvirringsmatrisen är relativt enkel att förstå, men den relaterade terminologin kan vara förvirrande.
Jag ville skapa en ”snabbreferensguide” för terminologi för förvirringsmatriser eftersom jag inte kunde hitta någon befintlig resurs som uppfyllde mina krav: kompakt i presentationen, med användning av siffror i stället för godtyckliga variabler, och förklarad både i formler och meningar.
Låt oss börja med ett exempel på en förvirringsmatris för en binär klassificerare (även om den lätt kan utvidgas till att omfatta fler än två klasser):
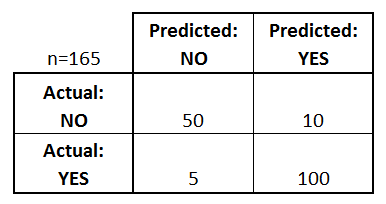
Vad kan vi lära oss av den här matrisen?
- Det finns två möjliga förutsägbara klasser: ”ja” och ”nej”. Om vi till exempel skulle förutsäga förekomsten av en sjukdom skulle ”ja” betyda att de har sjukdomen och ”nej” skulle betyda att de inte har sjukdomen.
- Klassificatorn gjorde totalt 165 förutsägelser (t.ex, 165 patienter testades för förekomst av den sjukdomen).
- Utav dessa 165 fall förutspådde klassificeraren ”ja” 110 gånger och ”nej” 55 gånger.
- I verkligheten har 105 patienter i urvalet sjukdomen och 60 patienter har inte sjukdomen.
Låt oss nu definiera de mest grundläggande termerna, som är hela tal (inte procentsatser):
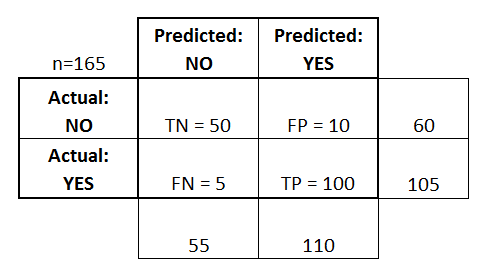
- true positives (TP): Dessa är fall där vi förutspådde ja (de har sjukdomen), och de har verkligen sjukdomen.
- true negatives (TN): Dessa är fall där vi förutspådde ja (de har sjukdomen), och de har faktiskt sjukdomen.
- true negatives (TN): Vi förutspådde nej, och de har inte sjukdomen.
- falskt positiva (FP): Vi förutspådde ja, men de har faktiskt inte sjukdomen. (Även känt som ett ”typ I-fel”.)
- falskt negativa (FN): Vi förutspådde nej, men de har faktiskt sjukdomen. (Även kallat ”typ II-fel”.)
Jag har lagt till dessa termer i förvirringsmatrisen och även lagt till rad- och kolonnsumman:
Det här är en lista över värden som ofta beräknas från en förvirringsmatris för en binär klassificerare:
- Noggrannhet:
- (TP+TN)/total = (100+50)/165 = 0,91
- Felklassificeringsgrad:
- (FP+FN)/total = (10+5)/165 = 0,09
- ekvivalent med 1 minus noggrannhet
- också känd som ”felprocent”
- Sannpositivprocent: När det faktiskt är ja, hur ofta förutsäger den ja?
- TP/aktuellt ja = 100/105 = 0,95
- också känd som ”känslighet” eller ”återkallelse”
- Falskt positivt resultat: När det faktiskt är nej, hur ofta förutspår den ja?
- FP/aktuellt nej = 10/60 = 0,17
- Sann negativ frekvens: När det faktiskt är nej, hur ofta förutsäger det nej?
- TN/aktuellt nej = 50/60 = 0,83
- ekvivalent med 1 minus False Positive Rate
- också känt som ”Specificity”
- Precision: När den förutsäger ja, hur ofta har den rätt?
- TP/predicted yes = 100/110 = 0,91
- Prevalens:
- Faktiskt ja/total = 105/165 = 0,64
Ett par andra termer är också värda att nämna:
- Nollfelprocent: Detta är hur ofta du skulle ha fel om du alltid förutspådde majoritetsklassen. (I vårt exempel skulle nollfelprocenten vara 60/165=0,36, eftersom om du alltid förutspådde ja skulle du bara ha fel i de 60 fallen med nej). Detta kan vara ett användbart baslinjemått att jämföra din klassificerare mot. Den bästa klassificeraren för en viss tillämpning kommer dock ibland att ha en högre felprocent än nollfelprocenten, vilket framgår av Accuracy Paradox.
- Cohens Kappa: Detta är i huvudsak ett mått på hur väl klassificeraren presterade jämfört med hur väl den skulle ha presterat helt enkelt av en slump. Med andra ord kommer en modell att ha en hög Kappa-poäng om det finns en stor skillnad mellan noggrannheten och nollfelprocenten. (Mer information om Cohens Kappa.)
- F-poäng: Detta är ett viktat genomsnitt av den sant positiva andelen (recall) och precisionen. (Mer information om F-poäng.)
- ROC-kurva: Detta är en vanligt förekommande graf som sammanfattar en klassificerares prestanda över alla möjliga tröskelvärden. Den skapas genom att plotta den sant positiva andelen (y-axeln) mot den falskt positiva andelen (x-axeln) när du varierar tröskelvärdet för att tilldela observationer till en viss klass. (Mer information om ROC-kurvor.)
Och slutligen, för dig som kommer från den bayesianska statistikens värld, här är en snabb sammanfattning av dessa termer från Applied Predictive Modeling:
I förhållande till bayesiansk statistik är sensitivitet och specificitet de betingade sannolikheterna, prevalensen är prioriteten och de positiva/negativa förutspådda värdena är de posteriora sannolikheterna.
Vill du veta mer?
I min nya 35-minuters video, Making sense of the confusion matrix, förklarar jag dessa begrepp mer ingående och tar upp mer avancerade ämnen:
- Hur man beräknar precision och recall för problem med flera klasser
- Hur man analyserar en 10-klassig förvirringsmatris
- Hur man väljer rätt utvärderingsmått för sitt problem
- Varför noggrannhet ofta är ett missvisande mått
Säg till om du har några frågor!