Lärandemål
1. Konvertera från en enhet till en annan enhet av samma typ.
I avsnitt 2.2 ”Uttrycka enheter” visade vi några exempel på hur man kan ersätta inledande enheter med andra enheter av samma typ för att få ett numeriskt värde som är lättare att förstå. I det här avsnittet kommer vi att formalisera processen.
Tänk på ett enkelt exempel: Hur många fot finns det i 4 yards? De flesta människor kommer nästan automatiskt att svara att det finns 12 fot på 4 yards. Hur gjorde du detta? Tja, om det finns 3 fot på en meter och det finns 4 meter, så finns det 4 × 3 = 12 fot på 4 meter.
Detta är naturligtvis korrekt, men det är informellt. Låt oss formalisera det på ett sätt som kan tillämpas mer allmänt. Vi vet att 1 yard (yd) är lika med 3 fot (ft):
1 yd = 3 ft
I matematiken kallas detta uttryck för en likhet. Algebrareglerna säger att du kan ändra (dvs. multiplicera eller dividera eller addera eller subtrahera) likheten (så länge du inte dividerar med noll) och det nya uttrycket kommer fortfarande att vara en likhet. Om vi till exempel delar båda sidorna med 2 får vi
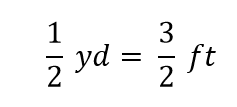
Vi ser att en halv yard är lika med 3/2, eller en och en halv fot – något som vi också vet är sant, så ovanstående ekvation är fortfarande en likhet. Om vi återgår till den ursprungliga likheten, antar vi att vi delar båda sidor av ekvationen med 1 yard (antal och enhet):
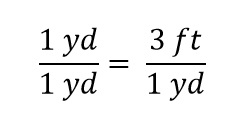
Uttrycket är fortfarande en likhet, enligt algebraens regler. Det vänstra bråket är lika med 1. Det har samma mängd i täljaren och nämnaren, så det måste vara lika med 1. Mängderna i täljaren och nämnaren upphäver varandra, både antalet och enheten:
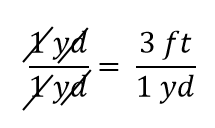
När allt upphävs i ett bråk reduceras bråket till 1:
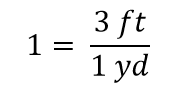
Vi har ett uttryck, 3 ft1 yd, som är lika med 1. Det är ett konstigt sätt att skriva 1, men det är logiskt: 3 ft är lika med 1 yd, så kvantiteterna i täljaren och nämnaren är samma kvantitet, bara uttryckt med olika enheter. Uttrycket 3 ft1 yd kallas konverteringsfaktor och används för att formellt ändra enheten för en kvantitet till en annan enhet. (Processen att omvandla enheter på ett sådant formellt sätt kallas ibland för dimensionsanalys eller faktoretikettmetoden.)
För att se hur detta sker, låt oss börja med den ursprungliga kvantiteten:
4 yd
Nu ska vi multiplicera denna kvantitet med 1. När du multiplicerar något med 1 ändrar du inte värdet på kvantiteten. I stället för att multiplicera med bara 1, låt oss skriva 1 som 3 ft1 yd:
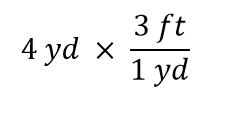
Termen 4 yd kan betraktas som 4 yd/1; det vill säga, den kan betraktas som ett bråk med 1 i nämnaren. Vi multiplicerar i huvudsak bråk. Om samma sak förekommer i täljaren och nämnaren i ett bråk upphävs de. I det här fallet är det enheten yard som upphävs:
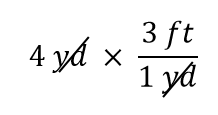
Det är allt vi kan upphäva. Multiplicera och dividera nu alla tal för att få fram det slutliga svaret: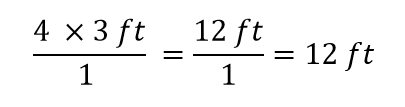
Även här får vi ett svar på 12 ft, precis som vi gjorde från början. Men i det här fallet använde vi ett mer formellt förfarande som kan tillämpas på en mängd olika problem.
Hur många millimeter är det i 14,66 m? För att svara på detta måste vi konstruera en omräkningsfaktor mellan millimeter och meter och tillämpa den korrekt på den ursprungliga kvantiteten. Vi börjar med definitionen av en millimeter, som är
1 mm = 1/1 000 m
Den 1/1 000 är vad prefixet milli- betyder. De flesta människor är mer bekväma med att arbeta utan bråk, så vi skriver om ekvationen genom att föra in 1 000 i täljaren på andra sidan av ekvationen:
1 000 mm = 1 m
Nu konstruerar vi en omräkningsfaktor genom att dividera en kvantitet i båda sidorna. Men nu uppstår en fråga: vilken kvantitet dividerar vi med? Det visar sig att vi har två val, och de två valen ger oss olika omräkningsfaktorer, som båda är lika med 1:
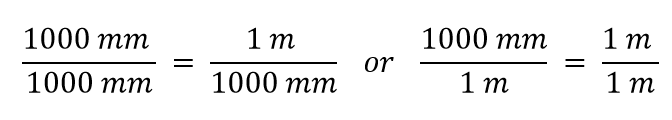
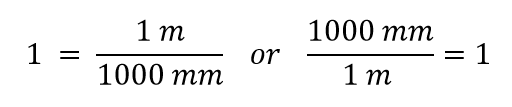
Vilken omräkningsfaktor ska vi använda? Svaret baseras på vilken enhet du vill bli av med i din ursprungliga kvantitet. Den ursprungliga enheten i vår kvantitet är meter, som vi vill konvertera till millimeter. Eftersom den ursprungliga enheten antas finnas i täljaren vill vi, för att bli av med den, ha meterenheten i nämnaren; då kommer de att upphävas. Därför kommer vi att använda den andra omvandlingsfaktorn. Genom att annullera enheterna och utföra matematiken får vi
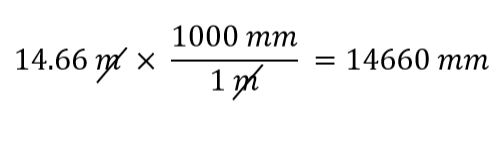
Bemärk hur m annulleras, vilket lämnar kvar mm, som är den intressanta enheten.
Förmågan att konstruera och tillämpa korrekta omräkningsfaktorer är en mycket kraftfull matematisk teknik i kemi. Du måste behärska denna teknik om du ska lyckas i denna och framtida kurser.
Exempel 7
- Konvertera 35,9 kL till liter.
- Konvertera 555 nm till meter.
Lösning
-
Vi kommer att använda det faktum att 1 kL = 1 000 L. Av de två omräkningsfaktorer som kan definieras är den som fungerar 1 000 L/1 kL. Om vi tillämpar denna omräkningsfaktor får vi
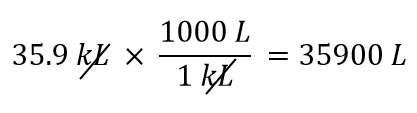
-
Vi kommer att använda oss av det faktum att 1 nm = 1/1 000 000 000 000 000 m, vilket vi kommer att skriva om till 1 000 000 000 000 000 nm = 1 m, eller 109 nm = 1 m. Av de två möjliga omräkningsfaktorerna har den som är lämplig enheten nm i nämnaren: 1 m/109 nm. Genom att tillämpa denna omräkningsfaktor får vi
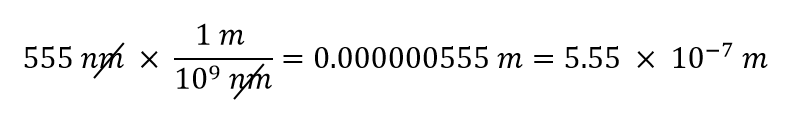
I det sista steget uttryckte vi svaret i vetenskaplig notation.
Testa dig själv
- Konvertera 67.08 μL till liter.
- Konvertera 56,8 m till kilometer.
Svar
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Hur blir det om vi har en härledd enhet som är en produkt av mer än en enhet, till exempel m2? Anta att vi vill konvertera kvadratmeter till kvadratcentimeter? Nyckeln är att komma ihåg att m2 betyder m × m, vilket innebär att vi har två meterenheter i vår härledda enhet. Det betyder att vi måste inkludera två omvandlingsfaktorer, en för varje enhet. För att till exempel konvertera 17,6 m2 till kvadratcentimeter utför vi konverteringen på följande sätt:
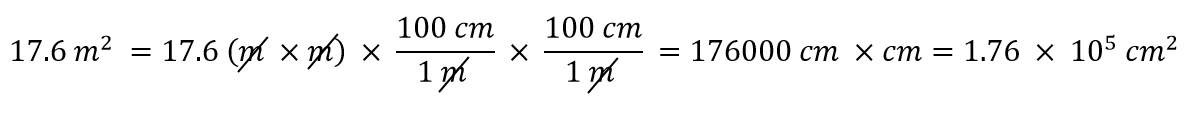
Exempel 8
Hur många kubikcentimeter finns i 0.883 m3?
Lösning
Med en exponent på 3 har vi tre längdenheter, så i förlängningen måste vi använda tre omvandlingsfaktorer mellan meter och centimeter. Vi har alltså
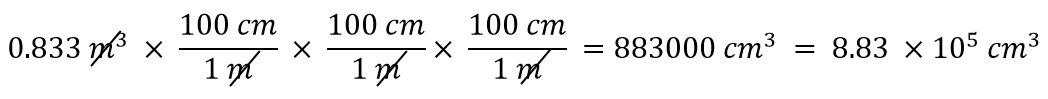
Du bör demonstrera för dig själv att de tre meterenheterna faktiskt upphävs.
Testa dig själv
Hur många kubikmillimeter finns det i 0,0923 m3?
Svar
9,23 × 107 mm3
Förutsatt att enheten du vill omvandla finns i nämnaren av en härledd enhet; vad händer då? I konverteringsfaktorn måste då den enhet som du vill ta bort finnas i täljaren. Detta kommer att upphäva den ursprungliga enheten i nämnaren och införa en ny enhet i nämnaren. Följande exempel illustrerar denna situation:
Exempel 9
Konvertera 88,4 m/min till meter/sekund.
Lösning
Vi vill ändra enheten i nämnaren från minuter till sekunder. Eftersom det finns 60 sekunder i 1 minut (60 s = 1 min) konstruerar vi en omvandlingsfaktor så att enheten vi vill ta bort, minuter, finns i täljaren: 1 min/60 s. Tillämpa och utför matematiken:
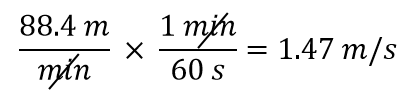
Bemärk hur 88,4 automatiskt hamnar i täljaren. Det beror på att vilket tal som helst kan ses som att det står i täljaren i ett bråk dividerat med 1.
Testa dig själv
Konvertera 0,203 m/min till meter/sekund.
Svar
0.00338 m/s eller 3,38 × 10-3 m/s
Figur 2.8 Hur snabbt är snabbt?
