Introduktion
Enzymernas aktiva platser består vanligen av aminosyrarester; beroende på vilka aminosyrarester som finns kan substratets specificitet variera kraftigt. Beroende på pH-nivån kan de fysiska egenskaperna (främst den elektriska laddningen) hos ett enzym förändras. En förändring av den elektriska laddningen kan förändra interaktionen mellan aminosyraresterna på den aktiva platsen och det inkommande substratet. Med detta sagt kan substratet binda till den aktiva platsen via vätebindning eller van der Waals-krafter. När substratet binder till den aktiva platsen bildar det ett enzym-substratkomplex som sedan deltar i ytterligare kemiska reaktioner.
För att ett enzym ska vara aktivt och energimässigt gynnsamt för att en kemisk reaktion ska kunna fortskrida måste ett substrat binda till enzymets ”aktiva plats”. En aktiv plats kan ses som ett lås och substratet som en nyckel; detta är känt som lås- och nyckelmodellen. Nyckeln (substratet) måste sättas in och vridas (kemisk reaktion), varefter låset (enzymet) öppnas (produktion av produkter). Observera att ett enzym kan ha mer än en aktiv plats. En annan teori om förhållandet mellan aktiv plats och substrat är teorin om inducerad anpassning, som är raka motsatsen till lås- och nyckelteorin (där den aktiva platsen är till synes oflexibel). I teorin om induced fit är enzymets aktiva plats mycket flexibel och ändrar bara sin konformation när substratet binder till den.
Enzymer fungerar som en katalysator genom att sänka Gibbs fria energi för aktivering av enzym-substratkomplexet. Nedan finns två figurer som visar en grundläggande enzymatisk reaktion med och utan katalysator:
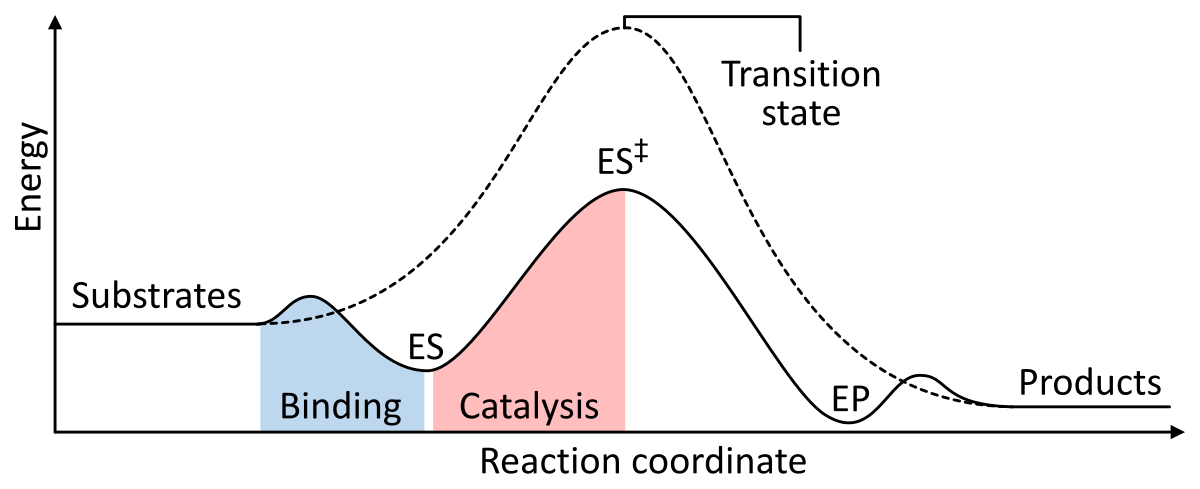
Figur 1: Energierna för stegen i en kemisk reaktion. Utan katalysator (streckad linje) behöver substratet mycket aktiveringsenergi för att nå ett övergångstillstånd, som sedan sönderfaller till produkter med lägre energi. När enzymet katalyseras (heldragen linje) binder enzymet substraten (ES) och stabiliserar sedan övergångstillståndet (ES‡) för att minska den aktiveringsenergi som krävs för att producera produkter (EP) som slutligen frigörs. från Wikipedia.
Enzymets effektivitet kan bestämmas på följande sätt: Betrakta en enkel enzymatisk reaktion:
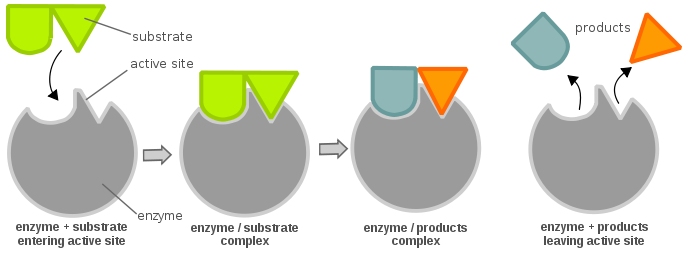
Den tyska biokemisten Leonor Michaelis och den kanadensiska biokemisten Maud Menten har härlett en ekvation som beskriver detta system, senare känd som ”Michaelis-Menten-ekvationen”, som visas nedan:
\}{K_M + } \tag{1}\]
Denna ekvation ger reaktionshastigheten vid en given substratkoncentration, om man antar en känd Vmax, som är den maximala hastighet som reaktionen kan fortskrida med, och KM, Michaelis-konstanten. I en praktisk tillämpning av Michaelis-Menten-ekvationen mäts dock ofta V0 och Vmax observeras som en mättnad eller platå i en dataplott. Eftersom substratkoncentrationen är känd är KM vanligtvis det beräknade värdet av intresse.
För \(K_M\), anta \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}}{2} = V_{max} \tag{3}\]
\ = \dfrac{V_{max}}{\dfrac{V_{max}}{2}}} \tag{4} \]
\ = 2 \tag{5}\]
\ \tag{6}\]
Michaeliskonstanten kan ses som hastigheten med vilken substratet lossnar från enzymet, vilket antingen kan inträffa när substrat-enzymkomplexet blir produkten eller när substratet lossnar från enzymet. KM kan visas som en ekvation:
\
Varvid k-1 är den hastighetskonstant vid vilken substratet blir obundet till enzymet, vilket resulterar i dissociation av enzym-substratkomplexet, k2 är den hastighetskonstant vid vilken substrat-enzymkomplexet försvinner och förvandlas till en produkt, och K1 är hastighetskonstanten för bildandet av substrat-enzymkomplexet. KM kan därför ses som hastigheten för substrat-enzymkomplexets försvinnande dividerat med hastigheten för substrat-enzymkomplexets bildande, vilket är den nivå vid vilken hälften av substratet är bundet till enzymet. KM är en användbar indikator för närvaron av en hämmare eftersom vi kan titta på förändringar i KM och jämföra med vår kontroll (biologiska system som vi vet inte har någon hämmare). KM är en beroende variabel och dess värde kan förändras av många orsaker, bland annat systemets pH-värde, temperatur eller andra förhållanden som kan påverka en kemisk reaktion. En liten KM indikerar att substratet har en hög affinitet för enzymet.
Michaelis-Menten-ekvationen är mest användbar för att mäta enzymeffektiviteten om v0 plottas mot , enligt följande:
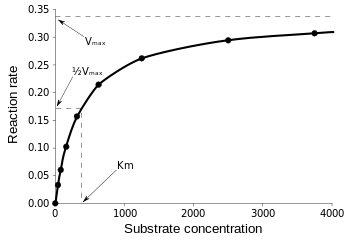
Figur 3: Diagram över reaktionshastighet och Michaelis-Menten-konstant. från Wikipedia.
Vmax är den maximala hastigheten som reaktionen kan löpa, oavsett , vilket innebär att även om du tillsätter mer substrat kan reaktionen inte gå snabbare. Det beror på att vid Vmax är alla aktiva platser på enzymet upptagna. Efter alla förklaringar om olika former av enzymkinetiska ekvationer kommer vi fram till vår slutsats om katalytisk effektivitet. Om vi återknyter till figur 3 har vi:
\_o}{\dfrac{k_{-1} + k_2}{k_1} + }\right) \tag{8}\]
Notera att \(k_2\) beskriver en irreversibel reaktion i motsats till ett jämviktsuttryck, jämfört med k-1 och k1. k2 kallas här också kcat, enzymets katalytiska effektivitet. Från den tidigare diskussionen är v0 den uppmätta reaktionshastigheten, vilket är produktbildningen över tiden, så man kan dra slutsatsen att en ekvation skulle se ut på följande sätt:
\}{dt} = k_2_0 \tag{9}\]
Varvid 0 är den totala enzymkoncentrationen.
Det är också känt att VMax observeras när hela enzym-substratkomplexet försvinner och omvandlas till produkter, så vi kan göra följande antagande:
\_0 \tag{10} \]
och efter omarrangemang får vi denna ekvation:
\_0} \tag{11}\]
Detta är ekvationen för att beräkna katalytisk effektivitet, som ska användas efter att vi har fått data från experiment och efter att ha använt Michaelis-Mentens ekvation. Med en större kcat är enzymet effektivt eftersom det behövs mindre enzym.