Kompressibilitetsfaktor (gaser) - Knowino

Från Knowino

Detta är en kontrollerad version av denna sida

Jump till: Figur 1: Exempel på grafer över gasers kompressibilitetsfaktorer

Kompressibilitetsfaktorn (Z) är en användbar termodynamisk egenskap för att modifiera lagen för ideala gaser så att den tar hänsyn till beteendet hos verkliga gaser. Den är ett mått på hur mycket de termodynamiska egenskaperna hos en verklig gas avviker från dem som förväntas av en idealgas. Det kan ses som förhållandet mellan den faktiska volymen av en verklig gas och den volym som förutses av den ideala gasen vid samma temperatur och tryck som den faktiska volymen.

För en idealgas har Z alltid värdet 1. För verkliga gaser kan värdet avvika positivt eller negativt, beroende på effekten av gasens intermolekylära krafter. Ju närmare en verklig gas är sin kritiska punkt eller sin mättnadspunkt, desto större är gasens avvikelser från det ideala beteendet.

Den övre grafen i figur 1 illustrerar hur kompressibilitetsfaktorn varierar för olika gaser vid samma temperatur och tryck. Den nedre grafen illustrerar hur kompressibilitetsfaktorn för en gas (t.ex. metan) vid ett givet tryck varierar med temperaturen.

Denna artikel behandlar endast kompressibilitetsfaktorn för gaser och fördjupar sig inte i kompressibiliteten för vätskor eller ång-vätskeblandningar.

Innehåll

1 Fastställande av gasers kompressibilitetsvärden
- 1.1 Generaliserade grafer för kompressibilitetsfaktorer för rena gaser
- 1.2 Generaliserade grafer för kompressibilitetsfaktorer för gasblandningar
- 1.3 Van der Waals-ekvationen
  - 1.3.1 Modifierade versioner av van der Waals-ekvationen
    - 1.3.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Virial ekvation för tillståndsförhållanden
- 1.5 Andra ekvationer för tillståndsförhållanden
- 1.6 Notation för gaskonstanten
2 Referenser

Bestämning av gasers kompressibilitetsvärden

Den ideala gaslagen definieras som:

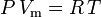
$P\,V_\mathrm{m} = R\,T$

och den ideala gaslagen korrigerad för icke-idealitet definieras som:

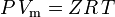
$P\,V_\mathrm{m} = ZR\,T$

varvid:
P	= tryck
Vm	= gasens molära volym
Z	= Komprimeringsfaktor
R	= Universalgaskonstant
T	= temperatur

och därmed:

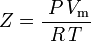
$Z = \frac{\;P\;P\,V_\mathrm{m}}{R\,T}$

vilket är den enklaste och mest använda tillståndsekvationen för verkliga gaser (EOS). Den största begränsningen med denna tillståndsekvation är att komprimerbarhetsfaktorn Z inte är en konstant utan varierar från en gas till en annan samt med temperaturen och trycket för den aktuella gasen. Den måste bestämmas experimentellt.

När experimentella data finns tillgängliga för specifika gaser kan dessa data användas för att ta fram grafer (t.ex. i figur 1) över Z mot trycket vid en konstant temperatur eller över Z mot trycket för olika temperaturer för dessa specifika gaser. Sådana grafer är användbara för att lätt få fram interpolerade värden för Z mellan de experimentellt bestämda värdena.

Kompressibilitetsfaktorn kan som tidigare nämnts också uttryckas som:

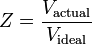
$Z = \frac{V_\mathrm{actual}}{V_\mathrm{ideal}}$

Det finns tre regimer som påverkar kompressibilitetsfaktorn:

värdet av Z tenderar mot 1 när gastrycket närmar sig 0, där alla gaser tenderar mot idealt beteende
värdet av Z är mindre än 1 vid mellanliggande tryck eftersom de intermolekylära attraktionskrafterna gör att de faktiska volymerna är mindre än de ideala värdena
värdet av Z är större än 1 och tenderar slutligen mot oändligheten. vid höga tryck eftersom de intermolekylära repulsiva krafterna gör att de faktiska volymerna blir större än idealvärdena

Generaliserade grafer över kompressibilitetsfaktorn för rena gaser

Det unika förhållandet mellan kompressibilitetsfaktorn och den reducerade temperaturen, Tr, och det reducerade trycket, Pr, uppmärksammades först av van der Waals 1873 och är känt som principen om motsvarande tillstånd med två parametrar. Principen om motsvarande tillstånd uttrycker generaliseringen att de egenskaper hos en gas som är beroende av intermolekylära krafter är relaterade till gasens kritiska egenskaper på ett universellt sätt. Detta ger en mycket viktig grund för att utveckla korrelationer av molekylära egenskaper.

När det gäller gasers kompressibilitet anger principen om motsvarande tillstånd att varje ren gas vid samma reducerade temperatur, Tr, och reducerade tryck, Pr, bör ha samma kompressibilitetsfaktor.

Den reducerade temperaturen och trycket definieras som:

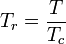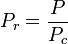
$T_r = \frac{T}{T_c}$ och $P_r = \frac{P}{P_c}$

Tc och Pc är kända som kritisk temperatur och kritiskt tryck för en gas. De är karakteristiska för varje specifik gas där Tc är den temperatur över vilken det inte är möjligt att göra en viss gas flytande och Pc är det lägsta tryck som krävs för att göra en viss gas flytande vid dess kritiska temperatur. Tillsammans definierar de den kritiska punkten för en vätska över vilken det inte finns några skilda flytande och gasformiga faser i en viss vätska.

Tryck-volym-temperaturdata (PVT) för verkliga gaser varierar från en ren gas till en annan. När kompressibilitetsfaktorerna för olika gaser med en enda komponent visas grafiskt mot trycket tillsammans med temperaturisotermer (vilket visas för metan i den nedre grafen i figur 1) uppvisar många av graferna liknande isotermiska former.

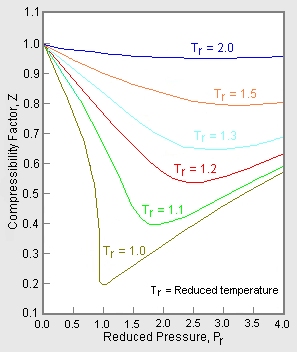
Figur 2: Exempel på en generaliserad graf över kompressibilitetsfaktorn

För att erhålla en generaliserad graf som kan användas för många olika gaser, används det reducerade trycket och den reducerade temperaturen, Pr och Tr, för att normalisera data om kompressibilitetsfaktorer. Figur 2 är ett exempel på en generaliserad graf över kompressibilitetsfaktorn som härrör från hundratals experimentella P-V-T-datapunkter för 10 rena gaser, nämligen metan, etan, etylen, propan, n-butan, i-pentan, n-hexan, kväve, koldioxid och ånga.

Det finns mer detaljerade generaliserade grafer för kompressibilitetsfaktorer som baseras på så många som 25 eller fler olika rena gaser, till exempel Nelson-Obert-graferna. Sådana grafer sägs ha en noggrannhet inom 1-2 procent för Z-värden större än 0,6 och inom 4-6 procent för Z-värden på 0,3-0,6.

De generaliserade graferna för kompressibilitetsfaktorer kan ha betydande fel för starkt polära gaser, vilket är gaser för vilka centrumen för positiv och negativ laddning inte sammanfaller. I sådana fall kan uppskattningen av Z vara felaktig med så mycket som 15-20 procent.

Kvantgaserna väte, helium och neon överensstämmer inte med beteendet för motsvarande tillstånd och det reducerade trycket och den reducerade temperaturen för dessa tre gaser bör omdefinieras på följande sätt för att förbättra noggrannheten i förutsägelsen av deras kompressibilitetsfaktorer när man använder de generaliserade graferna:

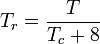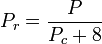
$T_r = \frac{T}{T_c + 8}$ och $P_r = \frac{P}{P_c + 8}$

där temperaturerna är i grader Kelvin och trycken i atmosfärer.

Generaliserade grafer för kompressibilitetsfaktorer för gasblandningar

De generaliserade graferna för kompressibilitetsfaktorer för rena gaser (såsom de exemplifieras i figur 2 eller Nelson-Obert-graferna kan också användas för gasblandningar med hjälp av Kays regel som föreslogs av W. B. Kay 1936. Denna regel förutsäger P-V-T-beteendet hos en gasblandning genom att bestämma kompressibilitetsfaktorn för en gasblandning vid reducerad temperatur och reducerat tryck definierade i termer av den pseudokritiska temperaturen Tpc och det pseudokritiska trycket Ppc, vilka definieras som:

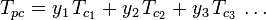
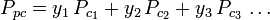
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_c_2} + y_3\,T_{c_3}\,\dots$ $P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_c_2} + y_3\,P_{c_3}\,\dots$

var:
Tpc	= den pseudokritiska temperaturen för gasblandningen
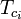$T_{c_i}$	= den kritiska temperaturen för en komponent i gasblandningen
Ppc	= den pseudokritiska temperaturen för en komponent i gasblandningen. trycket i gasblandningen
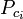$P_{c_i}$	= den kritiska temperaturen för en av gasens beståndsdelar
yi	= mol- (eller volym-) fraktionen av en av gasens beståndsdelar

den pseudoreducerade temperaturen, Tpr, och det pseudoreducerade trycket, Ppr, som ska användas med de generaliserade graferna för kompressibilitetsfaktorer för rena gaser är då:

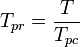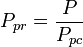
$T_{pr} = \frac{T}{T_{pc}}$ och $P_{pr} = \frac{P}{P_{pc}}$

En kompressibilitetsfaktorgrafik för naturgas (som är en blandning av kolväten och andra gaser) med pseudoreducerade temperaturer och tryck finns tillgänglig på Internet.

Van der Waals ekvation

Van der Waals ekvation utvecklades 1873 och kan uttryckas som:

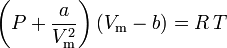
$\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T$

varvid:

a är ett mått på attraktionsstyrkan mellan gasmolekylerna b står för den volym som upptas av gasmolekylerna, vilket minskar den tillgängliga öppna volymen

Van der Waals ekvation kan omformas till följande:

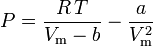
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

och komprimerbarhetsfaktorn kan skrivas som:

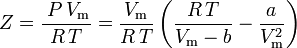
$Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\left(\frac{R\,T}{V_\mathrm{m}} - b} - \frac{a}{V_\mathrm{m}^2}\right)$

och vi har nu en ekvation för att bestämma Z med hjälp av van der Waals parametrarna a och b:

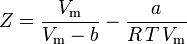
$Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}$

Och även om a och b kallas ”Van der Waals-konstanter” är de inte riktigt konstanter eftersom de varierar från en gas till en annan; de är dock oberoende av P, V och T. Med andra ord är de konstanta för den gas som betraktas. Givet den kritiska temperaturen och det kritiska trycket för en specifik gas kan a och b fås för den specifika gasen från dessa ekvationer:

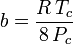
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ och $b = \frac{R\, T_c}{8\, P_c}$

Till exempel är det kritiska trycket för etan 4.884 MPa och den kritiska temperaturen är 305,43 K (32,3˚C). Med hjälp av den universella gaskonstanten R på 8,3145 Pa m3 K-1 mol-1 ger ovanstående ekvationer a = 0,557 m6 Pa mol-2 och b = 6,500×10-5 m3 mol-1.

Tabellerade värden för a och b för olika gaser finns i dessa referenser samt i många andra källor i den tekniska litteraturen.

Modifierade versioner av van der Waals ekvation

Bestämning av kompressibilitetsfaktorer med hjälp av van der Waals tillståndsekvation är en förbättring jämfört med att använda de generaliserade kompressibilitetsdiagrammen. Det finns dock modifierade versioner av van der Waals tillståndsekvation som ger en ännu större förbättring. De kanske vanligaste tillståndsekvationerna som används av ingenjörer som arbetar med oljeraffinering, petrokemisk produktion, behandling av naturgas, kryogen destillation och liknande industrier är Redlich-Kwong-ekvationen som utvecklades 1949, Soave-Redlich-Kwong-ekvationen som utvecklades 1972 och Peng-Robinson-ekvationen som utvecklades 1976. Dessa tre ekvationer är i huvudsak modifierade versioner av van der Waals-ekvationen. De jämförande ekvationerna är:

Redlich-Kwong

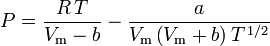
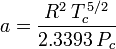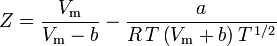
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}$ $a = \frac{R^2\, T_c^{\,5/2}}{2.3393\, P_c}$ och $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}$

Soave-Redlich-Kwong

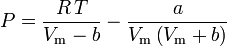
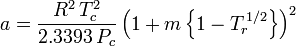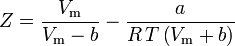
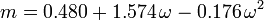
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)}$ $a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big\} \Big)^2$ och $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}$ $m = 0.480 + 1.574\, \omega - 0.176\, \omega^2$

Den acentriska faktorn, ω, som används som en parameter i Soave-Redlich-Kwong och Peng-Robinson ekvationerna introducerades för första gången av Pitzer et al 1955. Den kan uttryckas som:

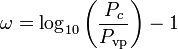
$\omega = \log_{10} \left(\frac{P_c}{P_\mathrm{vp}}\right) - 1$

där Pvp är gasens mättade ångtryck vid en temperatur på 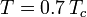$T = 0,7\, T_c$ .

Peng-Robinson

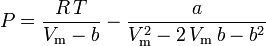
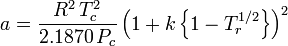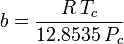
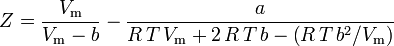
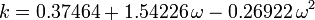
$P = \frac{R\,T}{V_\\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}$ $a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2$ och $b = \frac{R\, T_c}{12.8535\, P_c}$ $Z = \frac{V_\mathrm{m}}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}$ $k = 0.37464 + 1.54226\, \omega - 0.26922\, \omega^2$

Virial tillstånds ekvation

Den mest fundamentala tillstånds ekvationen, i och med att den har den mest solida teoretiska grunden, är virial tillstånds ekvation:

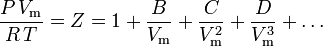
$\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots$

Den föreslogs först på empirisk grund av Thiesen 1885 och vidareutvecklades 1901 av Kamerlingh-Onnes. Ett statistiskt-mekaniskt uttryck för B härleddes först av Ornstein i hans doktorsavhandling. Ekvationen utvecklades därefter på nytt av H.D. Ursell 1927 på en teoretisk grund som härrörde från en statistisk-mekanisk (kluster) analys av intermolekylära krafter.

Parametrarna B, C och D kallas den andra, tredje respektive fjärde virialkoefficienten. Koefficienterna är inte konstanter eftersom de varierar från en gas till en annan samt med temperaturen hos den gas som studeras. De skrivs ibland som B(T), C(T) och D(T) för att ange att de är funktioner av temperaturen. Koefficienternas numeriska värde måste bestämmas experimentellt.

Den andra virialkoefficienten utgör den största delen av korrigeringen för gasens icke-ideala beteende. Av den anledningen avkortas virialekvationen ibland efter den term som innehåller den andra koefficienten. När den tredje koefficienten är tillgänglig brukar dock ekvationen vanligtvis trunkeras efter den term som innehåller den tredje koefficienten. Den fjärde koefficienten är sällan tillgänglig.

En omfattande sammanställning av virialkoefficienter för rena gaser och gasblandningar har utarbetats från virialkoefficientdatabasen vid Thermodynamics Research Center, tidigare vid Texas A&M University, College Station, Texas och numera belägen vid National Institute of Standards and Technology (NIST), Boulder, Colorado. Den senaste versionen av denna sammanställning publicerades 2003. NIST erbjuder också för köp en programvara, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), som innehåller andra och tredje virialkoefficienter samt en mängd andra termodynamiska egenskaper.

Andra tillståndsekvationer

Det finns ett antal andra tillståndsekvationer för att förutsäga beteendet hos verkliga gaser. De kanske mest kända är Beattie-Bridgeman-ekvationen som utvecklades 1929 och Benedict-Rubin-Webb-ekvationen som utvecklades 1940. I allmänhet är de mer komplexa än de ekvationer som diskuteras ovan.

Notation för gaskonstanten

Gaskonstanten som används i denna artikel är den universella gaskonstanten, R, som gäller för alla gaser. Det finns också en specifik gaskonstant, som kan betecknas Rs och definieras som Rs = R / M där M är molekylvikten.

Tyvärr använder många författare i den tekniska litteraturen ibland R som den specifika gaskonstanten utan att beteckna den som sådan eller ange att det är den specifika gaskonstanten. Detta kan och leder till förvirring.

1.0 1.1 1.1 1.2 1.3 1.4 McQuarrie, Donald A. och Simon, John D. (1999). Molekylär termodynamik. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.2 2.3 2.4 Yunus A. Çengal och Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, andra upplagan. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduktion till kemiteknisk termodynamik, sjunde upplagan. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.4 4.5 4.6 Y.V.C. Rao (1997). Termodynamik inom kemiteknik. Universities Press (Indien). ISBN 81-7371-048-1.
5.0 5.1 Gaslagar (föreläsning av professor M.J. Mombourquette vid Queens University, Kanada)
Hong Wei Xiang (2005). Principen om motsvarande stater och dess tillämpning: Termodynamiska, transport- och ytegenskaper hos vätskor. Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946). ”Modifierad lag om motsvarande tillstånd”. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Equations of State (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Equations of State (Föreläsningsmaterial använt av professor Sanford Klein vid University of Wisconsin-Madison, USA)
Richard W. Miller (1996). Handbok för flödesmätningsteknik, tredje upplagan. McGraw-Hill. ISBN 0-0-07-042366-0. (Se figur G-1 på sidan G.145)
Kai-Fui Vincent Wong (2000). Termodynamik för ingenjörer, första upplagan. CRC Press. ISBN 0-8493-0232-3. (Se figur A-2, sidan 278}
Nelson-Obert Generalized Compressibility Charts (Charts tillgängliga på Internet, från webbplatsen för San Diego State University, USA)
W.B.Kay (1936). ”Gaser och ångor vid hög temperatur och högt tryck – Densitet hos kolväten”. Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
Yunus A. Çengal och Michael A. Bowes (2005). Termodynamik: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Lecture material used by Professor R.M. Price at Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). Handbook of Chemistry and Physics, 56th Edition. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Chapter 3: Equations of State (pages 6-8 of 65 pdf pages) (Part of PhD thesis by Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
20.0 20.1 20.2 Jean Vidal (2003). Termodynamik: Tillämpningar inom kemiteknik och oljeindustrin. Editions Technip. ISBN 2-7108-0800-5.
Zakia Nasri och Housam Binous (2007). ”Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica”. Journal of Chemical Engineering of Japan 40 (6): 534-538. Hämtad härifrån.
K.S. Pitzer et al (1955). ”The Volumetric and Thermodynamic Properties of Fluids”. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning och Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
Max F. Thiesen (1885). ”Undersökningar av tillståndsekvationen”. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). ”Expression of the Equation of State of Gases and Liquids by Means of Series”. Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Tillämpning av Gibbs statistiska mekanik på molekylärteoretiska problem), Leiden
H. D. Ursell (1927). ”The Evaluation of Gibbs’ Phase Integral for Imperfect Gases” (23): 685.
J.D. Dymond och R.C. Wilhoit (författare), K.N. Marsch och M. Fenkel (redaktörer) (2003). Virialkoefficienter för rena gaser och blandningar, 1:a upplagan. Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie and O.C. Bridgeman (1929). ”A New Equation of State for Fluids”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb och L.C. Rubin (1940). ”An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures”. J. Chem. Phys. 8: 334-335.

En del av innehållet på denna sida kan tidigare ha funnits på Citizendium.

Hämtat från ”http://knowino.org/wiki/Compressibility_factor_(gases)”

Kategori: Fysik