Un automa cellulare è un insieme di celle “colorate” su una griglia di forma specifica che si evolve attraverso un numero di passi temporali discreti secondo un insieme di regole basate sugli stati delle celle vicine. Le regole sono poi applicate iterativamente per tutti i passi di tempo desiderati. von Neumann fu una delle prime persone a considerare un tale modello, e incorporò un modello cellulare nel suo “costruttore universale”. Gli automi cellulari sono stati studiati nei primi anni ’50 come un possibile modello per i sistemi biologici (Wolfram 2002, p. 48). Studi completi sugli automi cellulari sono stati eseguiti da S. Wolfram a partire dagli anni ’80, e la ricerca fondamentale di Wolfram nel campo è culminata nella pubblicazione del suo libro A New Kind of Science (Wolfram 2002) in cui Wolfram presenta una gigantesca collezione di risultati riguardanti gli automi, tra cui una serie di nuove scoperte rivoluzionarie.
L’episodio della stagione 2 “Scommettitore o peggio” (2006) del telefilm NUMB3RS menziona gli automi cellulari unidimensionali.
Gli automi cellulari sono disponibili in una varietà di forme e varietà. Una delle proprietà più fondamentali di un automa cellulare è il tipo di griglia su cui è calcolato. La “griglia” più semplice è una linea unidimensionale. In due dimensioni, si possono considerare griglie quadrate, triangolari ed esagonali. Gli automi cellulari possono anche essere costruiti su griglie cartesiane in un numero arbitrario di dimensioni, con il reticolo intero 
dimensionale 
come scelta più comune. Gli automi cellulari su un reticolo intero 
dimensionale sono implementati nel linguaggio Wolfram come CellularAutomaton.
Il numero di colori (o stati distinti) 
che un automa cellulare può assumere deve anche essere specificato. Questo numero è tipicamente un intero, con 
(binario) che è la scelta più semplice. Per un automa binario, il colore 0 è comunemente chiamato “bianco”, e il colore 1 è comunemente chiamato “nero”. Tuttavia, possono essere considerati anche automi cellulari che hanno una gamma continua di valori possibili.
Oltre alla griglia su cui vive un automa cellulare e ai colori che possono assumere le sue celle, deve essere specificato anche il quartiere in cui le celle si influenzano a vicenda. La scelta più semplice è quella dei “vicini più prossimi”, in cui solo le celle direttamente adiacenti ad una data cella possono essere influenzate ad ogni passo temporale. Due quartieri comuni nel caso di un automa cellulare bidimensionale su una griglia quadrata sono il cosiddetto quartiere di Moore (un quartiere quadrato) e il quartiere di von Neumann (un quartiere a forma di diamante).
Il tipo più semplice di automa cellulare è un automa binario, nearest-neighbor, unidimensionale. Tali automi sono stati chiamati “automi cellulari elementari” da S. Wolfram, che ha ampiamente studiato le loro sorprendenti proprietà (Wolfram 1983; 2002, p. 57). Ci sono 256 automi di questo tipo, ognuno dei quali può essere indicizzato da un unico numero binario la cui rappresentazione decimale è nota come la “regola” per quel particolare automa. Un’illustrazione della regola 30 è mostrata qui sopra insieme all’evoluzione che produce dopo 15 passi partendo da una singola cella nera.
Una classe leggermente più complicata di automi cellulari sono gli automi cellulari totalistici monodimensionali a più vicini, 
colori. In tali automi, è la media delle celle adiacenti che determina l’evoluzione, e i più semplici esempi non banali hanno 
colori. Per questi automi, l’insieme delle regole che descrivono il comportamento può essere codificato come un 
numero 
-ario conosciuto come “codice”. Le regole e i 300 passi dell’automa ternario (
) del codice 912 sono illustrati sopra.
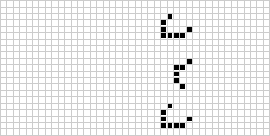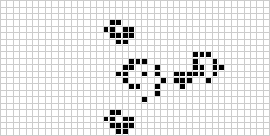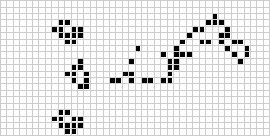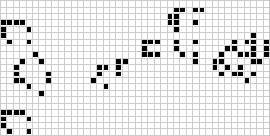
In due dimensioni, l’automa cellulare più conosciuto è il gioco della vita di Conway, scoperto da J. H. Conway nel 1970 e divulgato nelle colonne di Martin Gardner su Scientific American. Il gioco della vita è un automa cellulare binario (
) totalistico con un quartiere di Moore di range 
. Anche se il calcolo delle generazioni successive del gioco della vita è stato originariamente fatto a mano, la rivoluzione del computer è arrivata presto e ha permesso di studiare e propagare modelli più estesi. Un’animazione della costruzione del gioco della vita conosciuta come un treno puffer è illustrata sopra.
WireWorld è un altro comune automa cellulare bidimensionale.
La teoria degli automi cellulari è immensamente ricca, con semplici regole e strutture capaci di produrre una grande varietà di comportamenti inaspettati. Per esempio, esistono automi cellulari universali che sono in grado di simulare il comportamento di qualsiasi altro automa cellulare o macchina di Turing. È stato persino dimostrato da Gacs (2001) che esistono automi cellulari universali tolleranti agli errori, la cui capacità di simulare altri automi cellulari non è ostacolata da perturbazioni casuali, a condizione che tali perturbazioni siano sufficientemente rade.