Biografia

Brahmagupta (598-668 CE)
Il grande matematico e astronomo indiano del VII secolo Brahmagupta scrisse alcune importanti opere di matematica e astronomia. Veniva dallo stato del Rajasthan nel nord-ovest dell’India (è spesso indicato come Bhillamalacarya, il maestro di Bhillamala), e più tardi divenne il capo dell’osservatorio astronomico di Ujjain nell’India centrale. La maggior parte delle sue opere sono composte in versi ellittici, una pratica comune nella matematica indiana dell’epoca, e di conseguenza hanno qualcosa di poetico.
Sembra probabile che le opere di Brahmagupta, specialmente il suo testo più famoso, il “Brahmasphutasiddhanta”, siano state portate dal califfo abbaside dell’VIII secolo Al-Mansur al suo centro di apprendimento appena fondato a Baghdad, sulle rive del Tigri, fornendo un importante collegamento tra la matematica e l’astronomia indiana e la nascente ascesa della scienza e della matematica nel mondo islamico.
Nella sua opera sull’aritmetica, Brahmagupta spiegò come trovare il cubo e la radice cubica di un intero e diede regole che facilitavano il calcolo dei quadrati e delle radici quadrate. Ha anche dato regole per trattare cinque tipi di combinazioni di frazioni. Ha dato la somma dei quadrati dei primi n numeri naturali come n(n + 1)(2n + 1)⁄6 e la somma dei cubi dei primi n numeri naturali come (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Trattare lo zero come un numero

Le regole di Brahmagupta per trattare lo zero e i numeri negativi
Il genio di Brahmagupta, però, venne nel suo trattamento del concetto di (allora relativamente nuovo) numero zero. Anche se spesso attribuito al matematico indiano Bhaskara I del settimo secolo, il suo “Brahmasphutasiddhanta” è probabilmente il primo testo conosciuto a trattare lo zero come un numero a sé stante, piuttosto che come una semplice cifra segnaposto come facevano i babilonesi, o come un simbolo di mancanza di quantità come facevano i greci e i romani.
Brahmagupta stabilì le regole matematiche di base per trattare lo zero (1 + 0 = 1; 1 – 0 = 1; e 1 x 0 = 0), sebbene la sua comprensione della divisione per zero fosse incompleta (pensava che 1 ÷ 0 = 0). Quasi 500 anni dopo, nel XII secolo, un altro matematico indiano, Bhaskara II, mostrò che la risposta doveva essere infinito, non zero (sulla base del fatto che 1 può essere diviso in un numero infinito di pezzi di dimensione zero), una risposta che fu considerata corretta per secoli. Tuttavia, questa logica non spiega perché 2 ÷ 0, 7 ÷ 0, ecc, dovrebbe anche essere zero – l’opinione moderna è che un numero diviso per zero è in realtà “indefinito” (cioè non ha senso).
La visione di Brahmagupta dei numeri come entità astratta, piuttosto che solo per contare e misurare, gli permise di fare un altro enorme salto concettuale che avrebbe avuto profonde conseguenze per la matematica futura. In precedenza, la somma 3 – 4, per esempio, era considerata senza significato o, nel migliore dei casi, solo zero. Brahmagupta, tuttavia, si rese conto che poteva esistere una cosa come un numero negativo, che chiamò “debito” in opposizione a “proprietà”. Ha esposto le regole per trattare con i numeri negativi (ad esempio, un negativo per un negativo è un positivo, un negativo per un positivo è un negativo, ecc).
Inoltre, ha sottolineato, le equazioni quadratiche (del tipo x2 + 2 = 11, per esempio) potrebbero in teoria avere due possibili soluzioni, una delle quali potrebbe essere negativa, perché 32 = 9 e -32 = 9. Oltre al suo lavoro sulle soluzioni delle equazioni lineari generali e delle equazioni quadratiche, Brahmagupta andò ancora oltre considerando i sistemi di equazioni simultanee (insieme di equazioni contenenti più variabili), e risolvendo le equazioni quadratiche con due incognite, qualcosa che non fu nemmeno considerato in Occidente fino a mille anni dopo, quando Fermat stava considerando problemi simili nel 1657.
Teorema di Brahmagupta sui quadrilateri ciclici
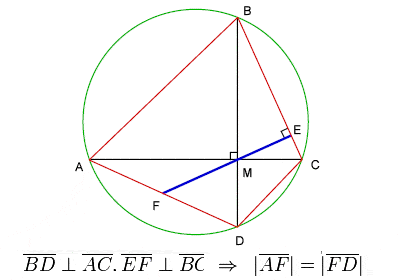
Teorema di Brahmagupta sui quadrilateri ciclici
Brahmagupta tentò persino di scrivere questi concetti piuttosto astratti, usando le iniziali dei nomi dei colori per rappresentare le incognite nelle sue equazioni, uno dei primi accenni di ciò che oggi conosciamo come algebra.
Brahmagupta dedicò una parte sostanziale del suo lavoro alla geometria e alla trigonometria. Stabilì √10 (3,162277) come una buona approssimazione pratica per π (3,141593), e diede una formula, ora nota come Formula di Brahmagupta, per l’area di un quadrilatero ciclico, così come un celebre teorema sulle diagonali di un quadrilatero ciclico, solitamente indicato come Teorema di Brahmagupta.
| << Torna a Matematica indiana | Avanti a Madhava >> |