Obiettivo di apprendimento
1. Convertire da un’unità a un’altra unità dello stesso tipo.
Nella Sezione 2.2 “Esprimere le unità”, abbiamo mostrato alcuni esempi di come sostituire le unità iniziali con altre unità dello stesso tipo per ottenere un valore numerico che sia più facile da comprendere. In questa sezione, formalizzeremo il processo.
Considerate un semplice esempio: quanti piedi ci sono in 4 iarde? La maggior parte delle persone risponderà quasi automaticamente che ci sono 12 piedi in 4 metri. Come avete fatto a fare questa determinazione? Bene, se ci sono 3 piedi in 1 iarda e ci sono 4 iarde, allora ci sono 4 × 3 = 12 piedi in 4 iarde.
Questo è corretto, naturalmente, ma è informale. Formalizziamolo in un modo che possa essere applicato più in generale. Sappiamo che 1 yard (yd) è uguale a 3 piedi (ft):
1 yd = 3 ft
In matematica, questa espressione si chiama uguaglianza. Le regole dell’algebra dicono che si può cambiare (cioè moltiplicare o dividere o aggiungere o sottrarre) l’uguaglianza (finché non si divide per zero) e la nuova espressione sarà ancora un’uguaglianza. Per esempio, se dividiamo entrambi i lati per 2, otteniamo
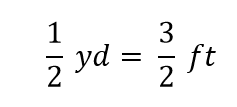
Vediamo che la metà di una yard è uguale a 3/2, o un piede e mezzo, qualcosa che sappiamo anche essere vero, quindi l’equazione di cui sopra è ancora un’uguaglianza. Tornando all’uguaglianza originale, supponiamo di dividere entrambi i lati dell’equazione per 1 iarda (numero e unità):
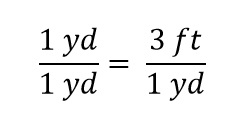
L’espressione è ancora un’uguaglianza, secondo le regole dell’algebra. La frazione di sinistra è uguale a 1. Ha la stessa quantità nel numeratore e nel denominatore, quindi deve essere uguale a 1. Le quantità nel numeratore e nel denominatore si annullano, sia il numero che l’unità:
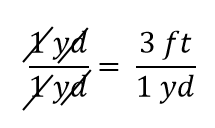
Quando tutto si annulla in una frazione, la frazione si riduce a 1:
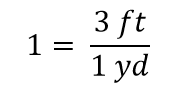
Abbiamo un’espressione, 3 ft1 yd, che è uguale a 1. Questo è un modo strano di scrivere 1, ma ha senso: 3 ft equivalgono a 1 yd, quindi le quantità nel numeratore e nel denominatore sono la stessa quantità, solo espressa con unità diverse. L’espressione 3 ft1 yd è chiamata fattore di conversione, e viene usata per cambiare formalmente l’unità di una quantità in un’altra unità. (Il processo di conversione delle unità in questo modo formale è a volte chiamato analisi dimensionale o metodo dell’etichetta del fattore.)
Per vedere come questo accade, iniziamo con la quantità originale:
4 yd
Ora moltiplichiamo questa quantità per 1. Quando si moltiplica qualcosa per 1, non si cambia il valore della quantità. Invece di moltiplicare solo per 1, scriviamo 1 come 3 ft1 yd:
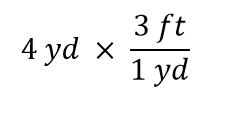
Il termine 4 yd può essere pensato come 4 yd/1; cioè, può essere pensato come una frazione con 1 nel denominatore. Stiamo essenzialmente moltiplicando frazioni. Se la stessa cosa appare nel numeratore e nel denominatore di una frazione, si annullano. In questo caso, ciò che si annulla è l’unità yard:
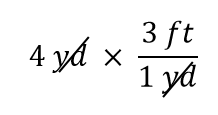
Questo è tutto ciò che possiamo annullare. Ora, moltiplichiamo e dividiamo tutti i numeri per ottenere la risposta finale: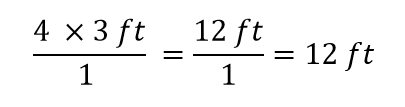
Ancora una volta, otteniamo una risposta di 12 ft, proprio come abbiamo fatto inizialmente. Ma in questo caso, abbiamo usato una procedura più formale che è applicabile a una varietà di problemi.
Quanti millimetri ci sono in 14,66 m? Per rispondere, dobbiamo costruire un fattore di conversione tra millimetri e metri e applicarlo correttamente alla quantità originale. Iniziamo con la definizione di millimetro, che è
1 mm = 1/1.000 m
L’1/1.000 è il significato del prefisso milli-. La maggior parte delle persone si trova più a suo agio lavorando senza frazioni, quindi riscriveremo questa equazione portando il 1.000 nel numeratore dell’altro lato dell’equazione:
1.000 mm = 1 m
Ora costruiamo un fattore di conversione dividendo una quantità in entrambi i lati. Ma ora sorge una domanda: per quale quantità dividiamo? Si scopre che abbiamo due scelte, e le due scelte ci daranno diversi fattori di conversione, entrambi uguali a 1:
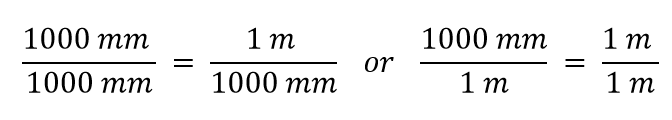
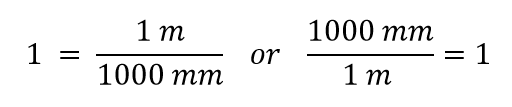
Quale fattore di conversione usiamo? La risposta si basa su quale unità si vuole eliminare nella quantità iniziale. L’unità originale della nostra quantità è metri, che vogliamo convertire in millimetri. Poiché l’unità originale si presume sia nel numeratore, per liberarcene vogliamo l’unità metro nel denominatore; poi si annulleranno. Pertanto, useremo il secondo fattore di conversione. Annullando le unità ed eseguendo la matematica, otteniamo
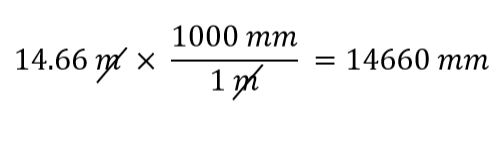
Nota come m si annulla, lasciando mm, che è l’unità di interesse.
La capacità di costruire e applicare fattori di conversione appropriati è una tecnica matematica molto potente in chimica. Devi padroneggiare questa tecnica se vuoi avere successo in questo e nei futuri corsi.
Esempio 7
- Convertire 35,9 kL in litri.
- Convertire 555 nm in metri.
Soluzione
-
Utilizzeremo il fatto che 1 kL = 1.000 L. Dei due fattori di conversione che possono essere definiti, quello che funziona è 1.000 L/1 kL. Applicando questo fattore di conversione, otteniamo
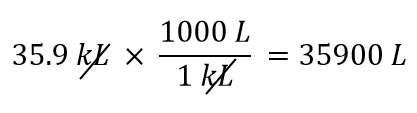
-
Utilizzeremo il fatto che 1 nm = 1/1.000.000.000 m, che riscriveremo come 1.000.000.000 nm = 1 m, o 109 nm = 1 m. Dei due possibili fattori di conversione, quello appropriato ha l’unità nm al denominatore: 1 m/109 nm. Applicando questo fattore di conversione, otteniamo
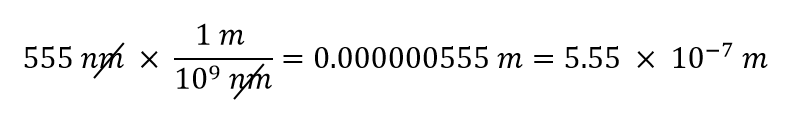
Nel passaggio finale, abbiamo espresso la risposta in notazione scientifica.
Test Yourself
- Converti 67.08 μL in litri.
- Convertire 56,8 m in chilometri.
Risposte
- 6,708 × 10-5 L
- 5,68 × 10-2 km
E se abbiamo un’unità derivata che è il prodotto di più unità, come m2? Supponiamo di voler convertire i metri quadrati in centimetri quadrati? La chiave è ricordare che m2 significa m × m, il che significa che abbiamo due unità di metri nella nostra unità derivata. Ciò significa che dobbiamo includere due fattori di conversione, uno per ogni unità. Per esempio, per convertire 17,6 m2 in centimetri quadrati, eseguiamo la conversione come segue:
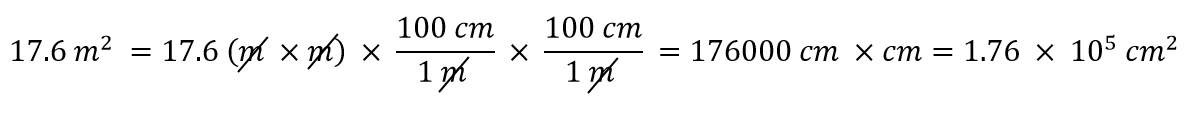
Esempio 8
Quanti centimetri cubi ci sono in 0.883 m3?
Soluzione
Con un esponente di 3, abbiamo tre unità di lunghezza, quindi per estensione dobbiamo usare tre fattori di conversione tra metri e centimetri. Così, abbiamo
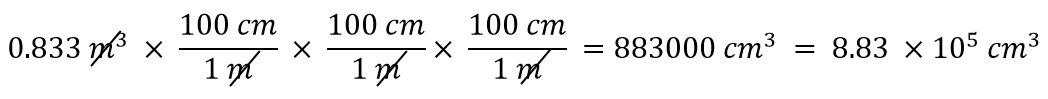
Devi dimostrare a te stesso che le tre unità di misura si annullano davvero.
Test Yourself
Quanti millimetri cubi sono presenti in 0,0923 m3?
Risposta
9,23 × 107 mm3
Supponiamo che l’unità che vuoi convertire sia nel denominatore di un’unità derivata; cosa allora? Allora, nel fattore di conversione, l’unità che si vuole rimuovere deve essere nel numeratore. Questo si annullerà con l’unità originale nel denominatore e introdurrà una nuova unità nel denominatore. Il seguente esempio illustra questa situazione.
Esempio 9
Convertire 88,4 m/min in metri/secondo.
Soluzione
Vogliamo cambiare l’unità nel denominatore da minuti a secondi. Poiché ci sono 60 secondi in 1 minuto (60 s = 1 min), costruiamo un fattore di conversione in modo che l’unità che vogliamo rimuovere, i minuti, sia al numeratore: 1 min/60 s. Applichiamo ed eseguiamo la matematica:
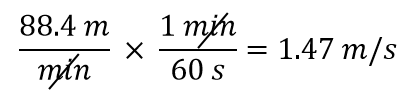
Nota come l’88.4 va automaticamente al numeratore. Questo perché qualsiasi numero può essere pensato come se fosse nel numeratore di una frazione diviso per 1.
Test Yourself
Convertire 0,203 m/min in metri/secondo.
Risposta
0.00338 m/s o 3,38 × 10-3 m/s
Figura 2.8 How Fast Is Fast?

Fonte: “Grapevine snail “di Jürgen Schoneris sotto licenza Creative Commons Attribution-Share Alike 3.0 Unported license.