Coordinate baricentriche

di
Geometria > CoordinateGeometria >
Geometria > Geometria piana > Triangoli > Proprietà dei triangoli >

Le coordinate baricentriche sono triple di numeri (t_1,t_2,t_3) corrispondenti a masse poste ai vertici di un triangolo di riferimento DeltaA_1A_2A_3. Queste masse determinano poi un punto P, che è il centroide geometrico delle tre masse ed è identificato con le coordinate (t_1,t_2,t_3). I vertici del triangolo sono dati da (1,0,0), (0,1,0), e (0,0,1). Le coordinate baricentriche furono scoperte da Möbius nel 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).

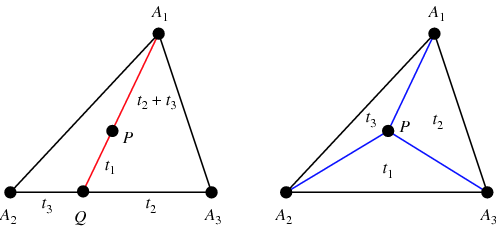
Barycentric

Per trovare le coordinate baricentriche di un punto arbitrario P, trovare t_2 e t_3 dal punto Q all’intersezione della linea A_1P con il lato A_2A_3, e poi determinare t_1 come la massa a A_1 che bilancerà una massa t_2+t_3 a Q, rendendo così P il centroide (figura a sinistra). Inoltre, le aree dei triangoli DeltaA_1A_2P, DeltaA_1A_3P, e DeltaA_2A_3P sono proporzionali alle coordinate baricentriche t_3, t_2, e t_1 di P (figura destra; Coxeter 1969, p. 217).

Le coordinate baricentriche sono omogenee, quindi

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

per mu!=0.

Le coordinate baricentriche normalizzate in modo che diventino le aree reali dei sottotriangoli sono chiamate coordinate baricentriche omogenee. Le coordinate baricentriche normalizzate in modo che

t_1+t_2+t_3=1,
(2)

in modo che le coordinate diano le aree dei sottotriangoli normalizzate per l’area del triangolo originale sono chiamate coordinate areali (Coxeter 1969, p. 218). Le coordinate baricentriche e areali possono fornire prove particolarmente eleganti di teoremi geometrici come il teorema di Routh, il teorema di Ceva e il teorema di Menelao (Coxeter 1969, pp. 219-221).

(Non necessariamente omogenee) le coordinate baricentriche per una serie di centri comuni sono riassunte nella tabella seguente. Nella tabella, a, b, e c sono le lunghezze dei lati del triangolo e s è il suo semiperimetro.

centro del triangolo coordinate baricentriche
circocentro O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
punto Gergonne Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
Nagel point Na (s-a,s-b,s-c)
ortocentro H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
punto simmetrico K (a^2,b^2,c^2)
centroide del triangolo G (1,1,1)

In coordinate baricentriche, una linea ha una equazione lineare omogenea. In particolare, la retta che unisce i punti (r_1,r_2,r_3) e (s_1,s_2,s_3) ha equazione

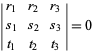|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 e 57; Coxeter 1969, p. 219; Bottema 1982). Se i vertici P_i di un triangolo DeltaP_1P_2P_3 hanno coordinate baricentriche (x_i,y_i,z_i), allora l’area del triangolo è

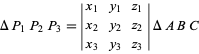DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Lascia un commento