Barycentrické souřadnice

autor:
Geometrie > Souřadnicová geometrie >
Geometrie > Rovinná geometrie > Trojúhelníky > Vlastnosti trojúhelníků >

Barycentrické souřadnice jsou trojice čísel (t_1,t_2,t_3) odpovídající hmotám umístěným ve vrcholech vztažného trojúhelníku DeltaA_1A_2A_3. Tyto hmotnosti pak určují bod P, který je geometrickým středem těchto tří hmotností a je identifikován souřadnicemi (t_1,t_2,t_3). Vrcholy trojúhelníku jsou dány souřadnicemi (1,0,0), (0,1,0) a (0,0,1). Barycentrické souřadnice objevil Möbius v roce 1827 (Coxeter 1969, s. 217; Fauvel et al. 1993).

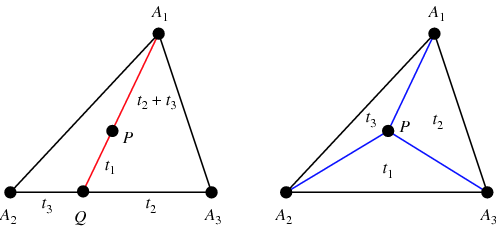
Barycentric

Chcete-li najít barycentrické souřadnice pro libovolný bod P, najděte t_2 a t_3 z bodu Q v průsečíku přímky A_1P se stranou A_2A_3, a pak určete t_1 jako těleso v bodě A_1, které vyváží těleso t_2+t_3 v bodě Q, čímž se P stane středem (levý obrázek). Dále jsou plochy trojúhelníků DeltaA_1A_2P, DeltaA_1A_3P a DeltaA_2A_3P úměrné barycentrickým souřadnicím t_3, t_2 a t_1 P (pravý obrázek; Coxeter 1969, str. 217).

Barycentrické souřadnice jsou homogenní, takže

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

pro mu!=0.

Barycentrické souřadnice normalizované tak, aby se staly skutečnými plochami podúhelníků, se nazývají homogenní barycentrické souřadnice. Barycentrické souřadnice normalizované tak, že

t_1+t_2+t_3=1,
(2)

tak, že souřadnice udávají plochy podúhelníků normalizované plochou původního trojúhelníku, se nazývají areálové souřadnice (Coxeter 1969, s. 218). Barycentrické a areálové souřadnice mohou poskytnout zvláště elegantní důkazy geometrických tvrzení, jako je Routhova věta, Cevova věta a Menelova věta (Coxeter 1969, s. 219-221).

(Ne nutně homogenní) barycentrické souřadnice pro řadu běžných středů shrnuje následující tabulka. V tabulce jsou a, b a c délky stran trojúhelníku a s je jeho poloměr.

střed trojúhelníku barycentrické souřadnice
obvodový střed O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a,b,c)
excenter J_B (a,-b,c)
excenter J_C (a,b,-c)
Gergonův bod Ge ((s-b)(s-c), (s-c)(s-a), (s-a)(s-b))
incenter I (a,b,c)
Nagelův bod Na (s-a,s-b,s-c)
ortocentr H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symetrický bod K (a^2,b^2,c^2)
centroid trojúhelníku G (1,1,1)

V barycentrických souřadnicích má přímka lineární homogenní rovnici. Konkrétně přímka spojující body (r_1,r_2,r_3) a (s_1,s_2,s_3) má rovnici

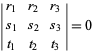|r_1 r_2 r_3; s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, str. 39 a 57; Coxeter 1969, s. 219; Bottema 1982). Jestliže vrcholy P_i trojúhelníku DeltaP_1P_2P_3 mají barycentrické souřadnice (x_i,y_i,z_i), pak plocha trojúhelníku je

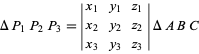DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000).

Napsat komentář