Jedná se o stochastické procesy učení s rekurentní strukturou, které jsou základem prvních optimalizačních technik používaných v ANN. Boltzmannův stroj vynalezli Geoffrey Hinton a Terry Sejnowski v roce 1985. Větší názornost lze vypozorovat z Hintonových slov o Boltzmannově stroji.
„Překvapivou vlastností této sítě je, že využívá pouze lokálně dostupné informace. Změna váhy závisí pouze na chování dvou jednotek, které spojuje, i když tato změna optimalizuje globální míru.“ – Ackley, Hinton 1985.
Několik důležitých bodů o Boltzmannově stroji –
-
Využívají rekurentní strukturu.
-
Skládají se ze stochastických neuronů, které mají jeden ze dvou možných stavů, buď 1, nebo 0.
-
Využívají rekurentní strukturu.
-
Některé neurony v ní jsou adaptivní (volný stav) a některé jsou upnuté (zamrzlý stav).
-
Pokud bychom na diskrétní Hopfieldovu síť aplikovali simulované žíhání, pak by se z ní stal Boltzmannův stroj.
Cíl Boltzmannova stroje
Hlavním cílem Boltzmannova stroje je optimalizace řešení problému. Úkolem Boltzmannova stroje je optimalizovat váhy a množství související s daným problémem.
Architektura
Následující schéma ukazuje architekturu Boltzmannova stroje. Z diagramu je zřejmé, že se jedná o dvourozměrné pole jednotek. Zde jsou váhy na propojeních mezi jednotkami -p, kde p > 0. Váhy vlastních propojení jsou dány b, kde b > 0.
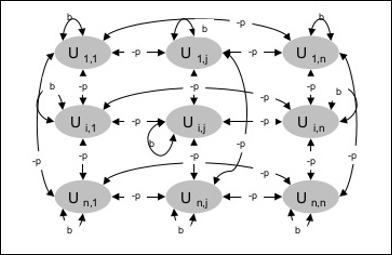
Tréninkový algoritmus
Jak víme, Boltzmannovy stroje mají pevné váhy, tudíž nebude existovat žádný tréninkový algoritmus, protože nepotřebujeme aktualizovat váhy v síti. Pro testování sítě však musíme nastavit váhy a také najít funkci shody (CF).
Boltzmannův stroj má množinu jednotek Ui a Uj a má na nich obousměrná spojení.
-
Uvažujeme pevnou váhu řekněme wij.
-
wij ≠ 0, pokud jsou Ui a Uj propojeny.
-
Existuje také symetrie ve váženém propojení, tj.tj. wij = wji.
-
wii také existuje, tj. existovalo by samopropojení mezi jednotkami.
-
Pro každou jednotku Ui by její stav ui byl buď 1, nebo 0.
Hlavním cílem Boltzmannova stroje je maximalizace konsenzuální funkce (CF), kterou lze zadat následujícím vztahem
$$CF\:=\:\displaystyle\sum\limits_{i}. \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Nyní, když se stav změní z 1 na 0 nebo z 0 na 1, pak změna konsensu může být dána následujícím vztahem –
$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Tady ui je aktuální stav Ui.
Změna koeficientu (1 – 2ui) je dána následujícím vztahem –
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}:je\:aktuálně\:off\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
Obvykle jednotka Ui nemění svůj stav, ale pokud ano, pak by informace byla lokální pro danou jednotku. S touto změnou by také došlo ke zvýšení konsensu sítě.
Pravděpodobnost, že síť přijme změnu stavu jednotky, je dána následujícím vztahem –
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$
Tady je T řídícím parametrem. Bude se snižovat, jakmile CF dosáhne maximální hodnoty.
Testovací algoritmus
Krok 1 – Pro zahájení trénování inicializujte následující –
- Váhy představující omezení problému
- Řídicí parametr T
Krok 2 – Pokračujte v krocích 3-8, pokud není splněna podmínka zastavení.
Krok 3 – Proveďte kroky 4-7.
Krok 4 – Předpokládejte, že jeden ze stavů změnil váhu, a zvolte celá čísla I, J jako náhodné hodnoty mezi 1 a n.
Krok 5 – Vypočítejte změnu konsensu takto –
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Krok 6 – Vypočítejte pravděpodobnost, že tato síť přijme změnu stavu
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp}$$
Krok 7 – Přijměte nebo odmítněte tuto změnu takto –
Případ I – pokud R < AF, změnu přijměte.
Případ II – pokud R ≥ AF, změnu zamítněte.
Zde je R náhodné číslo mezi 0 a 1.
Krok 8 – Snižte řídicí parametr (teplotu) následujícím způsobem –
T(new) = 0.95T(old)
Krok 9 – Otestujte podmínky zastavení, které mohou být následující –
- Teplota dosáhne zadané hodnoty
- Po zadaný počet iterací nedojde ke změně stavu
Reklama.
-