Buněčný automat

Buněčný automat je soubor „barevných“ buněk na mřížce určitého tvaru, který se vyvíjí v řadě diskrétních časových kroků podle souboru pravidel založených na stavech sousedních buněk. Pravidla se pak aplikují iterativně po libovolný počet časových kroků. von Neumann byl jedním z prvních, kdo o takovém modelu uvažoval, a buněčný model začlenil do svého „univerzálního konstruktoru“. Buněčné automaty byly studovány na počátku 50. let 20. století jako možný model biologických systémů (Wolfram 2002, s. 48). Komplexní studie buněčných automatů prováděl S. Wolfram od 80. let 20. století a Wolframův základní výzkum v této oblasti vyvrcholil vydáním knihy A New Kind of Science (Wolfram 2002), v níž Wolfram předkládá gigantickou sbírku výsledků týkajících se automatů, mezi nimiž je řada nových převratných objevů.

O jednorozměrných buněčných automatech se zmiňuje epizoda 2. série „Sázkař nebo něco horšího“ (2006) televizního kriminálního seriálu NUMB3RS.

Buněčné automaty mají různé tvary a odrůdy. Jednou z nejzákladnějších vlastností celulárního automatu je typ mřížky, na které se počítá. Nejjednodušší takovou „mřížkou“ je jednorozměrná čára. Ve dvou rozměrech lze uvažovat čtvercové, trojúhelníkové a šestiúhelníkové mřížky. Buněčné automaty lze také konstruovat na kartézských mřížkách v libovolném počtu rozměrů, přičemž nejčastější volbou je rozměrná celočíselná mřížka . Buněčné automaty na dimenzionální celočíselné mřížce jsou ve Wolframově jazyce implementovány jako CellularAutomaton.

Je třeba také zadat počet barev (nebo odlišných stavů) , které může buněčný automat nabývat. Toto číslo je obvykle celé číslo, přičemž (binární) je nejjednodušší volbou. U binárního automatu se barva 0 běžně nazývá „bílá“ a barva 1 se běžně nazývá „černá“. Lze však uvažovat i o celulárních automatech, které mají spojitý rozsah možných hodnot.

Kromě mřížky, na které celulární automat žije, a barev, které mohou jeho buňky nabývat, je třeba určit i okolí, ve kterém se buňky navzájem ovlivňují. Nejjednodušší volbou je „nejbližší sousedství“, kdy mohou být v každém časovém kroku ovlivněny pouze buňky přímo sousedící s danou buňkou. Dvě běžná okolí v případě dvourozměrného celulárního automatu na čtvercové mřížce jsou takzvané Moorovo okolí (čtvercové okolí) a von Neumannovo okolí (okolí ve tvaru kosočtverce).

Nejjednodušším typem celulárního automatu je binární jednorozměrný automat s nejbližšími sousedy. Takové automaty nazval S. Wolfram „elementárními celulárními automaty“, který se rozsáhle zabýval jejich úžasnými vlastnostmi (Wolfram 1983; 2002, s. 57). Existuje 256 takových automatů, z nichž každý lze indexovat jedinečným binárním číslem, jehož desítková reprezentace je známa jako „pravidlo“ pro daný automat. Ilustrace pravidla 30 je uvedena výše spolu s vývojem, který vytvoří po 15 krocích počínaje jedinou černou buňkou.

Mírně komplikovanější třídou celulárních automatů jsou jednorozměrné totalitní celulární automaty s nejbližším sousedem, barev. V takových automatech určuje vývoj průměr sousedních buněk a nejjednodušší netriviální příklady mají barev. U těchto automatů lze soubor pravidel popisujících chování zakódovat jako místné -ární číslo známé jako „kód“. Pravidla a 300 kroků ternárního () kódu automatu 912 jsou znázorněny výše.

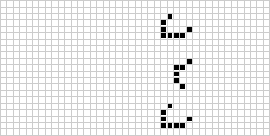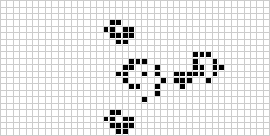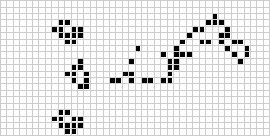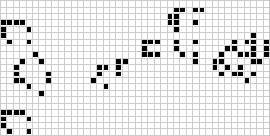
Ve dvou dimenzích je nejznámějším celulárním automatem Conwayova hra života, kterou objevil J. H. Conway v roce 1970 a kterou zpopularizoval Martin Gardner ve svých sloupcích v Scientific American. Hra o život je binární () totalitní celulární automat s Moorovým okolím o rozsahu . Ačkoli se výpočet po sobě jdoucích generací hry života původně prováděl ručně, brzy přišla počítačová revoluce, která umožnila studovat a šířit rozsáhlejší vzory. Výše je znázorněna animace konstrukce hry života známé jako puffer train.

WireWorld je další běžný dvourozměrný celulárníautomat.

Teorie celulárních automatů je nesmírně bohatá, přičemž jednoduchá pravidla a struktury jsou schopny vytvářet velké množství neočekávaných chování. Existují například univerzální celulární automaty, které jsou schopny simulovat chování jakéhokoli jiného celulárního automatu nebo Turingova stroje. Gacs (2001) dokonce dokázal, že existují univerzální celulární automaty odolné vůči poruchám, jejichž schopnosti simulovat jiné celulární automaty nebrání náhodné poruchy za předpokladu, že jsou tyto poruchy dostatečně řídké.

.