Faktor stlačitelnosti (plyny)

autor:
Z Knowino
Toto je ověřená verze této stránky

Přejít na:

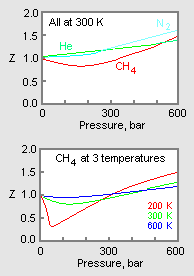
Obrázek 1: Příklady grafů faktorů stlačitelnosti plynu

Faktor stlačitelnosti (Z) je užitečná termodynamická vlastnost pro modifikaci zákona ideálního plynu, aby zohledňoval chování reálných plynů. Je to míra toho, jak moc se termodynamické vlastnosti reálného plynu odchylují od vlastností očekávaných u ideálního plynu. Lze si ji představit jako poměr skutečného objemu reálného plynu k objemu předpovězenému ideálním plynem při stejné teplotě a tlaku, jako je skutečný objem.

Pro ideální plyn má Z vždy hodnotu 1. U reálných plynů se může hodnota odchýlit kladně nebo záporně v závislosti na vlivu mezimolekulárních sil plynu. Čím blíže je reálný plyn svému kritickému bodu nebo bodu nasycení, tím větší jsou odchylky plynu od ideálního chování.

Horní graf na obrázku 1 znázorňuje, jak se mění faktor stlačitelnosti pro různé plyny při stejné teplotě a tlaku. Dolní graf znázorňuje, jak se faktor stlačitelnosti plynu (například metanu) při daném tlaku mění s teplotou.

Tento článek se zabývá pouze faktorem stlačitelnosti plynů a nezabývá se stlačitelností kapalin nebo směsí par a kapalin.

  • 1 Stanovení hodnot stlačitelnosti plynů
    • 1. Stlačitelnost plynů.1. Zobecněné grafy faktorů stlačitelnosti pro čisté plyny
    • 1.2. Zobecněné grafy faktorů stlačitelnosti pro směsi plynů
    • 1.3. Van der Waalsova rovnice
      • 1.3.1 Modifikované verze van der Waalsovy rovnice
        • 1.3.1.1 Redlich-Kwong
        • 1.3.1.2 Soave-Redlich-Kwong
        • 1.3.1.3 Peng-Robinson
    • 1.4 Viriální stavová rovnice
    • 1.5 Další stavové rovnice
    • 1.6 Zápis plynové konstanty
  • 2 Odkazy

Určení hodnot stlačitelnosti plynu

Zákon o ideálním plynu je definován jako:

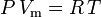
P\,V_\mathrm{m} = R\,T

a zákon ideálního plynu korigovaný na neideálnost je definován takto:

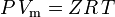
P\,V_\mathrm{m} = ZR\,T

kde:
P = tlak
Vm = molární objem plynu
Z = faktor stlačitelnosti
R = univerzální plynová konstanta
T = teplota

a tedy:

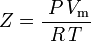
Z = \frac{\;P\,V_\mathrm{m}}{R\,T}

což je nejjednodušší a nejpoužívanější stavová rovnice reálného plynu (EOS). Hlavním omezením této stavové rovnice je, že faktor stlačitelnosti plynu, Z, není konstantní, ale mění se u jednotlivých plynů i v závislosti na teplotě a tlaku uvažovaného plynu. Musí být stanoven experimentálně.

Pokud jsou k dispozici experimentální údaje pro konkrétní plyny, lze je použít k vytvoření grafů (jako je obrázek 1) závislosti Z na tlaku při konstantní teplotě nebo závislosti Z na tlaku pro různé teploty těchto konkrétních plynů. Takové grafy jsou užitečné pro snadné získání interpolovaných hodnot Z mezi experimentálně stanovenými hodnotami.

Faktor stlačitelnosti, jak již bylo uvedeno, lze také vyjádřit takto:

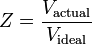
Z = \frac{V_\mathrm{aktuální}}{V_\mathrm{ideální}}

Existují tři režimy, které ovlivňují faktor stlačitelnosti:

  1. hodnota Z směřuje k 1, když se tlak plynu blíží k nule, kdy všechny plyny směřují k ideálnímu chování
  2. hodnota Z je při středních tlacích menší než 1, protože mezimolekulární přitažlivé síly způsobují, že skutečné objemy jsou menší než ideální hodnoty
  3. hodnota Z je větší než 1 a nakonec směřuje k nekonečnu při vysokých tlacích, protože mezimolekulární odpudivé síly způsobují, že skutečné objemy jsou větší než ideální hodnoty

Zobecněné grafy faktoru stlačitelnosti pro čisté plyny

Jedinečný vztah mezi faktorem stlačitelnosti a redukovanou teplotou, Tr a redukovaným tlakem, Pr, poprvé rozpoznal van der Waals v roce 1873 a je znám jako dvouparametrový princip odpovídajících stavů. Princip odpovídajících stavů vyjadřuje zobecnění, že vlastnosti plynu, které jsou závislé na mezimolekulárních silách, souvisejí s kritickými vlastnostmi plynu univerzálním způsobem. To poskytuje nejdůležitější základ pro vývoj korelací molekulárních vlastností.

Pokud jde o stlačitelnost plynů, princip odpovídajících stavů naznačuje, že každý čistý plyn při stejné redukované teplotě Tr a redukovaném tlaku Pr by měl mít stejný faktor stlačitelnosti.

Redukovaná teplota a tlak jsou definovány takto:

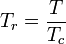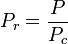
T_r = \frac{T}{T_c}aP_r = \frac{P}{P_c}

Tc a Pc jsou známy jako kritická teplota a kritický tlak plynu. Jsou to charakteristiky každého konkrétního plynu, přičemž Tc je teplota, nad kterou není možné daný plyn zkapalnit, a Pc je minimální tlak potřebný ke zkapalnění daného plynu při jeho kritické teplotě. Společně definují kritický bod kapaliny, nad kterým neexistují odlišné kapalné a plynné fáze dané kapaliny.

Údaje o tlaku-objemu-teplotě (PVT) pro reálné plyny se u jednotlivých čistých plynů liší. Když se však graficky znázorní faktory stlačitelnosti různých jednosložkových plynů v závislosti na tlaku spolu s teplotními izotermami (jak je znázorněno pro metan v dolním grafu na obrázku 1), mnoho grafů vykazuje podobné tvary izoterm.

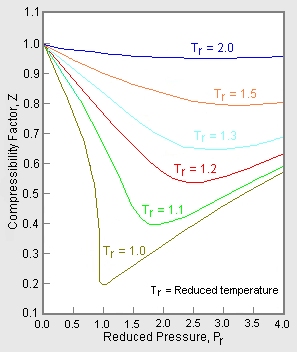
Obrázek 2: Příklad zobecněného grafu faktoru stlačitelnosti

Pro získání zobecněného grafu, který lze použít pro mnoho různých plynů, se k normalizaci údajů o faktoru stlačitelnosti používají redukované hodnoty tlaku a teploty, Pr a Tr. Na obrázku 2 je příklad zobecněného grafu faktoru stlačitelnosti získaného ze stovek experimentálních datových bodů P-V-T deseti čistých plynů, konkrétně metanu, ethanu, ethylenu, propanu, n-butanu, i-pentanu, n-hexanu, dusíku, oxidu uhličitého a páry.

Existují podrobnější zobecněné grafy faktoru stlačitelnosti založené až na 25 nebo více různých čistých plynech, například Nelson-Obertovy grafy. Uvádí se, že tyto grafy mají přesnost v rozmezí 1 až 2 % pro hodnoty Z větší než 0,6 a v rozmezí 4 až 6 % pro hodnoty Z 0,3 až 0,6.

Zobecněné grafy faktoru stlačitelnosti mohou být značně chybné pro silně polární plyny, což jsou plyny, u nichž se středy kladného a záporného náboje neshodují. V takových případech může být odhad pro Z chybný až o 15-20 %.

Kvantové plyny vodík, helium a neon neodpovídají chování odpovídajících stavů a redukovaný tlak a teplota pro tyto tři plyny by měly být nově definovány následujícím způsobem, aby se zlepšila přesnost předpovědi jejich faktorů stlačitelnosti při použití zobecněných grafů:

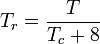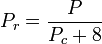
T_r = \frac{T}{T_c + 8}aP_r = \frac{P}{P_c + 8}

kde teploty jsou ve stupních Kelvina a tlaky v atmosférách.

Zobecněné grafy faktorů stlačitelnosti pro směsi plynů

Zobecněné grafy faktorů stlačitelnosti pro čisté plyny (jako je příklad na obrázku 2 nebo Nelson-Obertovy grafy lze použít také pro směsi plynů pomocí Kayova pravidla navrženého W. B. Kayem v roce 1936. Toto pravidlo předpovídá P-V-T chování směsi plynů určením faktoru stlačitelnosti pro směs plynů při snížené teplotě a sníženém tlaku definovaných jako pseudokritická teplota Tpc a pseudokritický tlak Ppc, které jsou definovány jako:

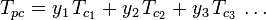
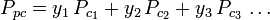
T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3}\,\dotsP_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3}\,\dots

.

kde:
Tpc = pseudokritická teplota směsi plynů
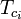T_{c_i} = kritická teplota složky plynné směsi
Ppc = pseudokritická teplota tlak plynné směsi
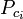P_{c_i} = kritická teplota složky plynu
yi = molární (nebo objemový) zlomek složky plynu

Pseudoredukovaná teplota, Tpr a pseudoredukovaný tlak Ppr, které se použijí s grafy zobecněného faktoru stlačitelnosti pro čisté plyny, jsou pak:

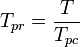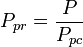
T_{pr} = \frac{T}{T_{pc}}aP_{pr} = \frac{P}{P_{pc}}

Na internetu je k dispozici graf faktoru stlačitelnosti pro zemní plyn (který je směsí uhlovodíku a jiných plynů) s použitím pseudoredukovaných teplot a tlaků.

Van der Waalsova rovnice

Van der Waalsova rovnice byla vyvinuta v roce 1873 a lze ji vyjádřit takto:

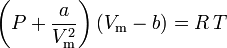
\left(P + \frac{a}{V_\mathrm{m}^2}\right)\left(V_\mathrm{m} - b\right) = R\,T

kde:

a je mírou síly přitažlivosti mezi molekulami plynu b zohledňuje objem obsazený molekulami plynu, což snižuje dostupný volný objem

Van der Waalsovu rovnici lze přeformulovat takto:

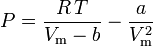
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}

a faktor stlačitelnosti lze zapsat jako:

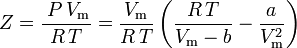
Z = \frac{\;P\,V_\mathrm{m}}{R\,T} = \frac{V_\mathrm{m}}{R\,T}\levice(\frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2}\pravice)

a nyní máme rovnici pro určení Z pomocí van der Waalsových parametrů a a b:

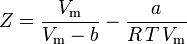
Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}

Ačkoli se a a a b označují jako „Van der Waalsovy konstanty“, nejsou to skutečné konstanty, protože se v jednotlivých plynech liší; jsou však nezávislé na P, V a T. Jinými slovy, jsou konstantní pro uvažovaný plyn. Vzhledem ke kritické teplotě a tlaku konkrétního plynu lze a a b pro tento konkrétní plyn získat z těchto rovnic:

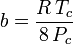
a = \frac{27\, R^2\, T_c^2}{64\, P_c}ab = \frac{R\, T_c}{8\, P_c}

Například kritický tlak ethanu je 4.884 MPa a kritická teplota je 305,43 K (32,3˚C). Při použití univerzální plynové konstanty R 8,3145 Pa m3 K-1 mol-1 dostaneme z výše uvedených rovnic a = 0,557 m6 Pa mol-2 a b = 6,500×10-5 m3 mol-1.

Tabulkové hodnoty a a b pro různé plyny jsou k dispozici v těchto odkazech i v mnoha dalších zdrojích odborné literatury.

Modifikované verze van der Waalsovy rovnice

Stanovení faktorů stlačitelnosti pomocí van der Waalsovy stavové rovnice představuje zlepšení oproti použití zobecněných tabulek stlačitelnosti. Existují však modifikované verze van der Waalsovy stavové rovnice, které poskytují ještě větší zlepšení. Snad nejčastěji používané stavové rovnice inženýry pracujícími v oblasti rafinace ropy, petrochemické výroby, zpracování zemního plynu, kryogenní destilace a příbuzných odvětvích jsou: Redlichova-Kwongova rovnice vyvinutá v roce 1949, Soaveova-Redlichova-Kwongova rovnice vyvinutá v roce 1972 a Pengova-Robinsonova rovnice vyvinutá v roce 1976. Tyto tři rovnice jsou v podstatě modifikovanými verzemi van der Waalsovy rovnice. Srovnávací rovnice jsou následující:

Redlich-Kwong

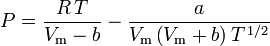
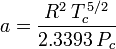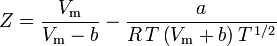
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}\left(V_\mathrm {m} + b\right)T^{\,1/2}}a = \frac{R^2\, T_c^{\,5/2}}{2.3393\, P_c}ab = \frac{R\, T_c}{11.5420\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)T^{\,1/2}}

Soave-Redlich-Kwong

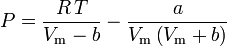
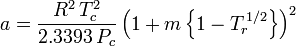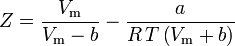
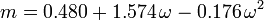
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}levá(V_\mathrm {m} + b\pravá)}a = \frac{R^2\,T_c^2}{2.3393\,P_c}\, \Big(1 + m\, \Big\{1 - T_r^{\,1/2} \Big\} \Big)^2ab = \frac{R\, T_c}{11.5420\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\, T\left(V_\mathrm {m} + b\right)}m = 0.480 + 1,574\, \omega - 0,176\, \omega^2

Acentrický faktor, ω, používaný jako parametr v Soave-Redlich-Kwongově a Peng-Robinsonově rovnici, byl poprvé zaveden Pitzerem a spol. v roce 1955. Lze jej vyjádřit takto:

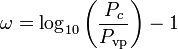
\omega = \log_{10}. \left(\frac{P_c}{P_\mathrm{vp}}\right) - 1

kde Pvp je tlak nasycených par plynu při teplotě 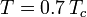T = 0,7\, T_c.

Peng-Robinson

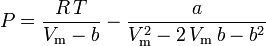
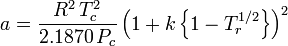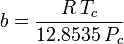
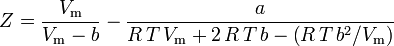
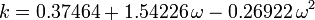
P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}\, b - b^2}a = \frac{R^2\,T_c^2}{2.1870\,P_c}\, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2ab = \frac{R\, T_c}{12,8535\, P_c}Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m} + 2\,R\,T\,b - \left(R\,T\, b^2/V_\mathrm{m}\right)}k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2

Viriální stavová rovnice

Nejzákladnější stavovou rovnicí, která má nejpevnější teoretický základ, je viriální stavová rovnice:

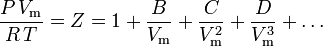
\frac{P\,V_\mathrm{m}}{R\,T} = Z = 1 + \frac{B}{V_\mathrm{m}} + \frac{C}{V_\mathrm{m}^2} + \frac{D}{V_\mathrm{m}^3} + \dots

Poprvé ji na empirickém základě navrhl Thiesen v roce 1885 a dále ji rozvinul v roce 1901 Kamerlingh-Onnes. Statisticko-mechanický výraz pro B poprvé odvodil Ornstein ve své doktorské práci. Rovnici následně přepracoval H. D. Ursell v roce 1927 na teoretickém základě odvozeném ze statisticko-mechanické (klastrové) analýzy mezimolekulárních sil.

Parametry B, C a D se označují jako druhý, třetí a čtvrtý viriální koeficient. Tyto koeficienty nejsou konstanty, protože se liší v závislosti na jednotlivých plynech i na teplotě uvažovaného plynu. Někdy se zapisují jako B(T), C(T) a D(T), aby se označilo, že jsou funkcemi teploty. Číselnou hodnotu koeficientů je třeba určit experimentálně.

Druhý viriální koeficient poskytuje největší část korekce na neideální chování plynu. Z tohoto důvodu se někdy viriální rovnice za členem obsahujícím druhý koeficient zkracuje. Pokud je však k dispozici třetí koeficient, rovnice se obvykle zkracuje za členem obsahujícím třetí koeficient. Čtvrtý koeficient je k dispozici jen zřídka.

Rozsáhlá kompilace viriálních koeficientů pro čisté plyny a směsi plynů byla připravena z databáze viriálních koeficientů ve Výzkumném centru termodynamiky, které dříve působilo na Texaské univerzitě A&M v College Station v Texasu a nyní se nachází v Národním institutu pro standardy a technologie (NIST) v Boulderu v Coloradu. Poslední verze této kompilace byla zveřejněna v roce 2003. NIST také nabízí ke koupi softwarový program NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), který obsahuje druhý a třetí viriální koeficient a řadu dalších termodynamických vlastností.

Další stavové rovnice

Existuje řada dalších stavových rovnic pro předpověď chování reálných plynů. Asi nejznámější jsou Beattieho-Bridgemanova rovnice vyvinutá v roce 1929 a Benedictova-Rubinova-Webbova rovnice vyvinutá v roce 1940. Obecně jsou složitější než výše uvedené rovnice.

Zápis plynové konstanty

Plynová konstanta používaná v tomto článku je univerzální plynová konstanta R, která platí pro jakýkoli plyn. Existuje také specifická plynová konstanta, kterou lze označit jako Rs a je definována jako Rs = R / M, kde M je molekulová hmotnost.

Naneštěstí mnoho autorů v odborné literatuře někdy používá R jako specifickou plynovou konstantu, aniž by ji takto označili nebo uvedli, že se jedná o specifickou plynovou konstantu. To může vést a vede k záměně.

  1. 1,0 1,1 1,2 1,3 1,4 McQuarrie, Donald A. a Simon, John D. (1999). Molekulární termodynamika. University Science Books. ISBN 1-891389-05-X.
  2. 2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal a Robert H. Turner (2004). Fundamentals of Thermal-Fluid Sciences, 2. vydání. McGraw-Hill Professional. ISBN 0-07-245426-1.
  3. 3.0 3.1 3.2 3.3 3.4 Smith, J.M. a další (2005). Introduction to Chemical Engineering Thermodynamics, Sedmé vydání. McGraw Hill. ISBN 0-07-310445-0.
  4. 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Chemická inženýrská termodynamika. Universities Press (Indie). ISBN 81-7371-048-1.
  5. 5.0 5.1 Plynové zákony (přednáška profesora M.J. Mombourquetta na Queens University, Kanada)
  6. Hong Wei Xiang (2005). Princip odpovídajících stavů a jeho uplatnění v praxi: Thermodynamic, Transport and Surface Properties of Fluids (Termodynamické, transportní a povrchové vlastnosti kapalin). Elsevier. ISBN 0-444-52062-7.
  7. Zlatá kniha IUPAC
  8. Gouq-Jen Su (1946). „Modifikovaný zákon odpovídajících stavů“. Průmyslová & inženýrská chemie 38 (8): 803-806. ISSN 0096-4484.
  9. 9.0 9.1 Stavové rovnice (profesor Lyes Kadem, Concordia University, Kanada)
  10. 10.0 10.1 Stavové rovnice (přednáškový materiál použitý profesorem Sanfordem Kleinem na University of Wisconsin-Madison, USA)
  11. Richard W. Miller (1996). Inženýrská příručka pro měření průtoku, 3. vydání. McGraw-Hill. ISBN 0-07-042366-0. (Viz obrázek G-1 na straně G.145)
  12. Kai-Fui Vincent Wong (2000). Thermodynamics for Engineers, 1. vydání. CRC Press. ISBN 0-8493-0232-3. (Viz obrázek A-2 na straně 278)
  13. Nelson-Obertovy zobecněné grafy stlačitelnosti (Grafy jsou k dispozici na internetu, z webových stránek San Diego State University, USA)
  14. W.B.Kay (1936). „Gases and Vapors At High Temperature and Pressure – Density of Hydrocarbon“ (Plyny a páry při vysoké teplotě a tlaku – hustota uhlovodíků). Industrial Engineering & Chemistry 28:1014. ISSN 0096-4484.
  15. Yunus A. Çengal a Michael A. Bowes (2005). Termodynamika: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
  16. Real Gases (Lecture material used by Professor R.M. Price at Christian Brothers University, U.S.A.)
  17. Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
  18. Robert C. Weast (Editor) (1975). Příručka chemie a fyziky, 56. vydání. CRC Press. ISBN 0-87819-455-X.
  19. 19.0 19.1 19.2 Chapter 3: Equations of State (pages 6-8 of 65 pdf pages) (Part of PhD thesis by Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
  20. 20.0 20.1 20.2 Jean Vidal (2003). Thermodynamics: The Thermodynamika: aplikace v chemickém inženýrství a ropném průmyslu. Editions Technip. ISBN 2-7108-0800-5.
  21. Zakia Nasri a Housam Binous (2007). „Applications of the Soave-Redlich-Kwong Equation of State Using Mathematica“. Journal of Chemical Engineering of Japan 40 (6): 534-538. Převzato odtud.
  22. K.S. Pitzer et al (1955). „The Volumetric and Thermodynamic Properties of Fluids“ (Objemové a termodynamické vlastnosti kapalin). Journal of the American Chemical Society 77: 3427-3440.
  23. Francis S. Manning a Richard E. Thompson (1991). Oilfield Processing of Petroleum (Zpracování ropy na ropných polích). Pennwell Books. ISBN 0-87814-343-2.
  24. Definice centrického faktoru (Physical Property Sources Index, PPSI, Švýcarského federálního technologického institutu v Curychu)
  25. Max F. Thiesen (1885). „Vyšetřování stavové rovnice“. Annalen der Physik und Chemie (24): 467-492.
  26. Heike Kamerlingh-Onnes (1901). „Expression of the Equation of State of Gases and Liquids by Means of Series“ (Vyjádření stavové rovnice plynů a kapalin pomocí řad). Commun. Phys. Lab. Leiden (71).
  27. S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Aplikace Gibbsovy statistické mechaniky na molekulárněteoretické problémy), Leiden
  28. H. D. Ursell (1927). „The Evaluation of Gibbs‘ Phase Integral for Imperfect Gases“ (Vyhodnocení Gibbsova fázového integrálu pro nedokonalé plyny) (23): 685.
  29. J. D. Dymond a R. C. Wilhoit (autoři), K. N. Marsch a M. Fenkel (editoři) (2003). Virial Coefficients of Pure gases and Mixtures, 1. vydání. Springer. ISBN 3-540-44340-1.
  30. NIST Standard Reference Database 23
  31. J.A. Beattie a O.C. Bridgeman (1929). „A New Equation of State for Fluids“ (Nová stavová rovnice pro kapaliny). Proc. Amer. Acad. Arts Sci. (63): 229-305.
  32. M. Benedict, G.B. Webb a L.C. Rubin (1940). „An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures“ (Empirická rovnice pro termodynamické vlastnosti lehkých uhlovodíků a jejich směsí). J. Chem. Phys. 8: 334-335.
Information.svg Některý obsah této stránky se již dříve mohl objevit na serveru Citizendium.
Převzato z „http://knowino.org/wiki/Compressibility_factor_(gases)“
Kategorie: Fyzika

Napsat komentář