Cíl výuky
1. Převést z jedné jednotky na jinou jednotku stejného typu
V části 2.2 „Vyjadřování jednotek“ jsme si ukázali několik příkladů, jak nahradit počáteční jednotky jinými jednotkami stejného typu a získat tak číselnou hodnotu, která je srozumitelnější. V této části tento postup formalizujeme.
Podívejte se na jednoduchý příklad: Kolik stop je ve 4 yardech? Většina lidí téměř automaticky odpoví, že ve 4 yardech je 12 stop. Jak jste toto určení provedli? No, pokud jsou na 1 yard 3 stopy a na 4 yardy jsou 4 stopy, pak je na 4 yardy 4 × 3 = 12 stop.
To je samozřejmě správně, ale je to neformální. Formalizujme ji způsobem, který lze použít obecněji. Víme, že 1 yard (yd) se rovná 3 stopám (ft):
1 yd = 3 ft
V matematice se tomuto výrazu říká rovnost. Pravidla algebry říkají, že rovnost můžete změnit (tj. vynásobit nebo vydělit nebo přičíst či odečíst) (pokud nedělíte nulou) a nový výraz bude stále rovností. Například vydělíme-li obě strany dvěma, dostaneme
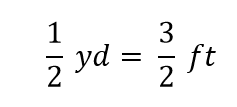
Vidíme, že polovina yardu se rovná 3/2 neboli jeden a půl stopy – což také víme, že je pravda, takže výše uvedená rovnice je stále rovností. Vrátíme-li se k původní rovnosti, předpokládejme, že obě strany rovnice vydělíme 1 yardem (číslem a jednotkou):
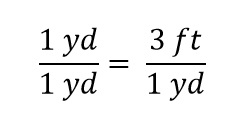
Výraz je podle pravidel algebry stále rovností. Levý zlomek se rovná 1. Má stejné množství v čitateli i jmenovateli, proto se musí rovnat 1. Veličiny v čitateli a jmenovateli se ruší, a to jak číslo, tak jednotka:
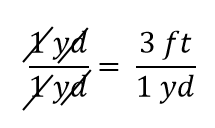
Když se ve zlomku vše ruší, zlomek se redukuje na 1:
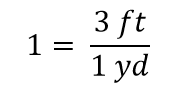
Máme výraz 3 ft1 yd, který se rovná 1. Je to zvláštní způsob zápisu 1, ale dává smysl: 3 ft se rovnají 1 yd, takže veličiny v čitateli a jmenovateli jsou stejné veličiny, jen vyjádřené jinými jednotkami. Výraz 3 ft1 yd se nazývá převodní koeficient a používá se k formální změně jednotky veličiny na jinou jednotku. (Proces převodu jednotek tímto formálním způsobem se někdy nazývá rozměrová analýza nebo metoda označování faktorů)
Abychom viděli, jak se to děje, začněme s původní veličinou:
4 yd
Nyní tuto veličinu vynásobíme 1. Když cokoli vynásobíme 1, hodnotu veličiny nezměníme. Místo toho, abychom násobili pouze 1, zapíšeme 1 jako 3 stopy1 yd:
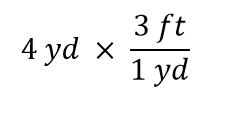
Výraz 4 yd si můžeme představit jako 4 yd/1; to znamená, že si ho můžeme představit jako zlomek s 1 ve jmenovateli. V podstatě násobíme zlomky. Pokud se v čitateli a jmenovateli zlomku vyskytuje stejná věc, ruší se. V tomto případě to, co se ruší, je jednotka yard:
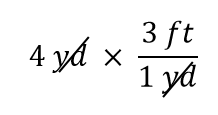
To je vše, co můžeme zrušit. Nyní všechna čísla vynásobíme a vydělíme, abychom dostali konečnou odpověď: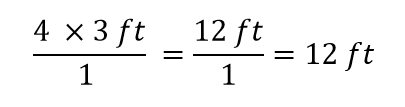
Znovu dostaneme odpověď 12 ft, stejně jako původně. V tomto případě jsme však použili formálnější postup, který je použitelný pro různé problémy.
Kolik milimetrů je v délce 14,66 m? Abychom mohli odpovědět, musíme sestrojit převodní koeficient mezi milimetry a metry a správně ho aplikovat na původní veličinu. Začneme definicí milimetru, která zní
1 mm = 1/1 000 m
Těch 1/1 000 znamená předpona mili-. Většině lidí se lépe pracuje bez zlomků, proto tuto rovnici přepíšeme tak, že 1 000 přeneseme do čitatele druhé strany rovnice:
1 000 mm = 1 m
Nyní sestrojíme převodní koeficient tak, že jednu veličinu rozdělíme na obě strany. Nyní však vyvstává otázka: kterou veličinou dělíme? Ukazuje se, že máme dvě možnosti a obě možnosti nám dají různé převodní koeficienty, přičemž oba se rovnají 1:
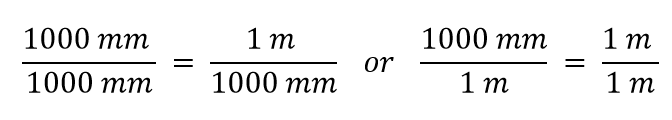
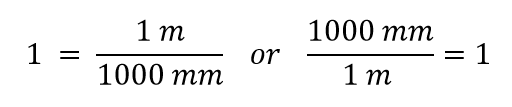
Který převodní koeficient použijeme? Odpověď vychází z toho, jaké jednotky se chceme zbavit ve výchozí veličině. Původní jednotkou naší veličiny jsou metry, které chceme převést na milimetry. Protože se předpokládá, že původní jednotka je v čitateli, chceme-li se jí zbavit, chceme jednotku metr ve jmenovateli; pak se zruší. Proto použijeme druhý převodní činitel. Zrušením jednotek a provedením matematických úkonů dostaneme
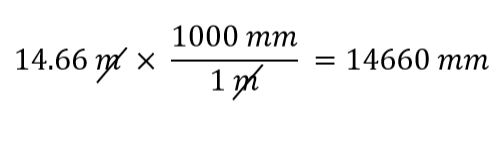
Všimněte si, jak se m ruší a zůstávají mm, což je jednotka, která nás zajímá.
Schopnost sestavit a použít správné převodní koeficienty je v chemii velmi mocnou matematickou technikou. Pokud chcete být úspěšní v tomto i budoucích kurzech, musíte tuto techniku ovládat.
Příklad 7
- Převeďte 35,9 kL na litry.
- Převeďte 555 nm na metry.
Řešení
-
Použijeme skutečnost, že 1 kL = 1 000 L. Ze dvou převodních koeficientů, které lze definovat, bude fungovat ten, který je 1 000 L/1 kL. Při použití tohoto převodního činitele dostaneme
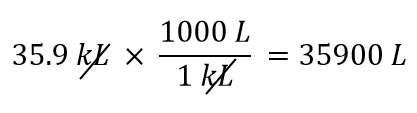
-
Použijeme skutečnost, že 1 nm = 1/1 000 000 000 m, což přepíšeme jako 1 000 000 000 nm = 1 m, nebo 109 nm = 1 m. Ze dvou možných převodních činitelů má ten vhodný ve jmenovateli jednotku nm: 1 m/109 nm. Při použití tohoto převodního činitele dostaneme
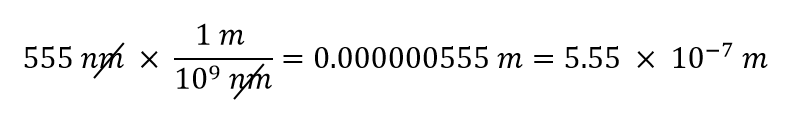
V posledním kroku jsme odpověď vyjádřili ve vědeckém zápisu.
Vyzkoušejte si
- Převod 67.08 μL na litry.
- Převeďte 56,8 m na kilometry.
Odpovědi
- 6,708 × 10-5 L
- 5,68 × 10-2 km
Co když máme odvozenou jednotku, která je součinem více jednotek, například m2? Předpokládejme, že chceme převést metry čtvereční na centimetry čtvereční? Klíčem je uvědomit si, že m2 znamená m × m, což znamená, že v naší odvozené jednotce máme dva metry. To znamená, že musíme zahrnout dva převodní koeficienty, pro každou jednotku jeden. Chceme-li například převést 17,6 m2 na čtvereční centimetry, provedeme převod takto:
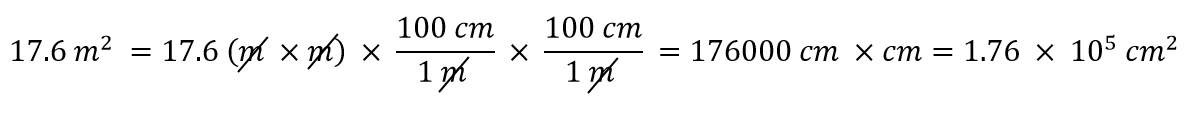
Příklad 8
Kolik centimetrů krychlových je v 0.883 m3?
Řešení
Při exponentu 3 máme tři délkové jednotky, takže následně musíme použít tři převodní koeficienty mezi metry a centimetry. Máme tedy
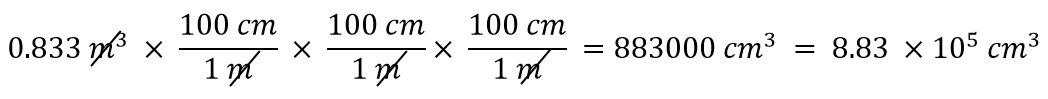
Měli byste si ukázat, že tři jednotky metrů se skutečně ruší.
Vyzkoušejte si
Kolik milimetrů krychlových je přítomno v 0,0923 m3
Odpověď
9,23 × 107 mm3
Předpokládejte, že jednotka, kterou chcete převést, je ve jmenovateli odvozené jednotky; jaká pak? Pak v převodním součiniteli musí být jednotka, kterou chcete odstranit, v čitateli. Tím se zruší původní jednotka ve jmenovateli a zavede se nová jednotka ve jmenovateli. Tuto situaci ilustruje následující příklad:
Příklad 9
Převod 88,4 m/min na metry/sekundu.
Řešení
Chceme změnit jednotku ve jmenovateli z minut na sekundy. Protože v 1 minutě je 60 sekund (60 s = 1 min), sestrojíme převodní koeficient tak, aby jednotka, kterou chceme odstranit, minuty, byla v čitateli: 1 min/60 s. Aplikujte a proveďte výpočet:
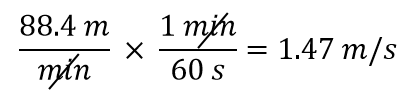
Všimněte si, jak 88,4 automaticky přechází do čitatele. To proto, že jakékoli číslo si můžeme představit jako číslo v čitateli zlomku dělené 1.
Vyzkoušejte si
Převeďte 0,203 m/min na metry/sekundu.
Odpověď
0.00338 m/s neboli 3,38 × 10-3 m/s
Obrázek 2.8 Jak rychlý je rychlý?

Zdroj: „Jürgen Schoneris pod licencí Creative Commons Attribution-Share Alike 3.0 Unported.
.