Matrice záměny je tabulka, která se často používá k popisu výkonnosti klasifikačního modelu (nebo „klasifikátoru“) na souboru testovacích dat, u nichž jsou známy pravdivé hodnoty. Samotná matice zmatení je poměrně jednoduchá na pochopení, ale související terminologie může být matoucí.
Chtěl jsem vytvořit „rychlou referenční příručku“ pro terminologii matice zmatení, protože jsem nemohl najít existující zdroj, který by vyhovoval mým požadavkům: kompaktní prezentace, použití čísel namísto libovolných proměnných a vysvětlení ve formě vzorců i vět.
Začněme příkladem matice záměny pro binární klasifikátor (i když ji lze snadno rozšířit na případ více než dvou tříd):
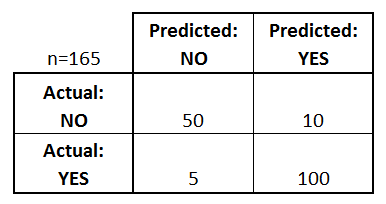
Co se z této matice můžeme dozvědět?
- Existují dvě možné predikované třídy: „ano“ a „ne“. Pokud bychom například předpovídali přítomnost nějaké nemoci, „ano“ by znamenalo, že danou nemoc mají, a „ne“ by znamenalo, že danou nemoc nemají.
- Klasifikátor provedl celkem 165 předpovědí (např, 165 pacientů bylo testováno na přítomnost dané nemoci).
- Z těchto 165 případů klasifikátor 110krát předpověděl „ano“ a 55krát „ne“.
- Ve skutečnosti 105 pacientů ve vzorku danou nemoc má a 60 pacientů ji nemá.
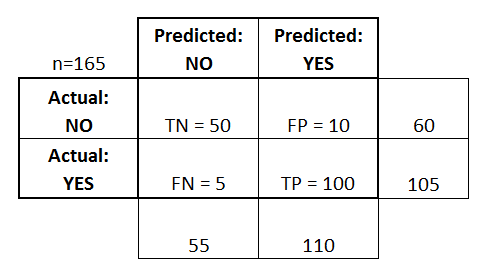
Definujme nyní nejzákladnější pojmy, které jsou celými čísly (nikoliv poměry):
- pravdivě pozitivní (TP):
- pravdivě negativní (TN):
- falešně pozitivní (FP): Předpověděli jsme, že ano, ale ve skutečnosti nemoc nemají. (Známé také jako „chyba typu I“.)
- falešně negativní (FN): Předpověděli jsme ne, ale ve skutečnosti nemoc mají. (Známé také jako „chyba typu II“.)
Doplnil jsem tyto výrazy do matice záměny a přidal také součty řádků a sloupců:
Toto je seznam sazeb, které se často počítají z matice záměny pro binární klasifikátor:
- Přesnost:
- (TP+TN)/celkem = (100+50)/165 = 0,91
- Míra chybné klasifikace:
- (FP+FN)/celkem = (10+5)/165 = 0,09
- ekvivalentní 1 minus Accuracy
- známá také jako „Error Rate“
- True Positive Rate: Když je to skutečně ano, jak často předpovídá ano?
- TP/skutečné ano = 100/105 = 0,95
- známý také jako „Sensitivity“ nebo „Recall“
- False Positive Rate: Když je to ve skutečnosti ne, jak často předpovídá ano?
- FP/skutečné ne = 10/60 = 0,17
- Míra pravdivé negativity: Když je to skutečně ne, jak často předpovídá ne?
- TN/skutečné ne = 50/60 = 0,83
- rovná se 1 minus míra falešně pozitivních výsledků
- známá také jako „specifičnost“
- Přesnost: Když předpovídá ano, jak často je správná?
- TP/předpovězené ano = 100/110 = 0,91
- Prevalence:
- skutečné ano/celkem = 105/165 = 0,64
Za zmínku stojí i několik dalších pojmů:
- Nulová chybovost: Jedná se o to, jak často byste se mýlili, kdybyste vždy předpovídali většinovou třídu. (V našem příkladu by nulová chybovost byla 60/165=0,36, protože kdybyste vždy předpovídali „ano“, mýlili byste se pouze v 60 případech „ne“). To může být užitečná základní metrika pro porovnání vašeho klasifikátoru. Nejlepší klasifikátor pro konkrétní aplikaci však někdy bude mít vyšší chybovost než nulová chybovost, jak ukazuje paradox přesnosti.
- Cohenovo kappa: Jedná se v podstatě o míru toho, jak dobře klasifikátor fungoval ve srovnání s tím, jak dobře by fungoval prostě náhodně. Jinými slovy, model bude mít vysoké skóre Kappa, pokud je velký rozdíl mezi přesností a nulovou chybovostí. (Další podrobnosti o Cohenově kappa.)
- F skóre: Jedná se o vážený průměr míry pravdivé pozitivity (recall) a přesnosti. (Další podrobnosti o skóre F.)
- Křivka ROC: Jedná se o běžně používaný graf, který shrnuje výkon klasifikátoru pro všechny možné prahové hodnoty. Vytváří se vykreslením poměru pravdivě pozitivních výsledků (osa y) a poměru falešně pozitivních výsledků (osa x) při změně prahové hodnoty pro přiřazení pozorování k dané třídě. (Další podrobnosti o křivkách ROC.)
A nakonec pro ty z vás, kteří jste ze světa bayesovské statistiky, přinášíme stručné shrnutí těchto pojmů z knihy Applied Predictive Modeling:
V souvislosti s bayesovskou statistikou jsou citlivost a specifičnost podmíněné pravděpodobnosti, prevalence je priorita a pozitivní/negativní předpovězené hodnoty jsou posteriorní pravděpodobnosti.
Chcete se dozvědět více?
V mém novém 35minutovém videu Making sense of the confusion matrix vysvětluji tyto pojmy hlouběji a zabývám se pokročilejšími tématy:
- Jak vypočítat přesnost a odvolávku pro problémy více tříd
- Jak analyzovat matici záměny 10 tříd
- Jak vybrat správnou metriku hodnocení pro váš problém
- Proč je přesnost často zavádějící metrikou
Dejte mi vědět, pokud máte nějaké otázky!