Úvod
Aktivní místa enzymů jsou obvykle tvořena aminokyselinovými zbytky; v závislosti na tom, které aminokyselinové zbytky jsou přítomny, se může značně lišit specifita substrátu. V závislosti na úrovni pH se mohou měnit fyzikální vlastnosti (především elektrický náboj) enzymu. Změna elektrického náboje může změnit interakci mezi aminokyselinovými zbytky aktivního místa a vstupujícím substrátem. Díky tomu se substrát může vázat na aktivní místo prostřednictvím vodíkové vazby nebo van der Waalsových sil. Jakmile se substrát naváže na aktivní místo, vytvoří komplex enzym-substrát, který se pak podílí na dalších chemických reakcích.
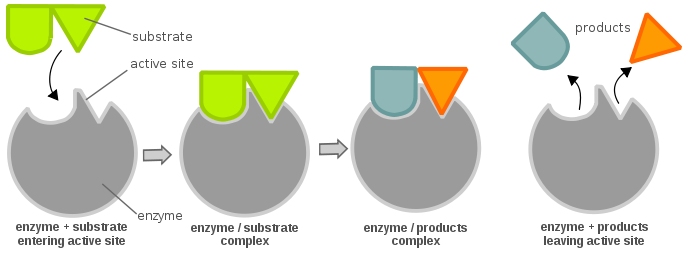
Aby byl enzym aktivní a energeticky příznivý, aby chemická reakce mohla pokračovat, musí se substrát vázat na „aktivní místo“ enzymu. Aktivní místo si lze představit jako zámek a substrát jako klíč; tento model je znám jako model zámku a klíče. Klíč (substrát) musí být vložen a otočen (chemická reakce), poté se zámek (enzym) otevře (produkce produktů). Všimněte si, že enzym může mít více než jedno aktivní místo. Další teorií o vztahu aktivního místa a substrátu je teorie indukovaného uložení, která je zcela opačná než teorie zámku a klíče (kde je aktivní místo zdánlivě nepružné). Podle teorie indukovaného přizpůsobení je aktivní místo enzymu velmi flexibilní a mění svou konformaci pouze tehdy, když se na něj naváže substrát.
Enzymy fungují jako katalyzátor tím, že snižují Gibbsovu volnou energii aktivace komplexu enzym-substrát. Níže jsou uvedeny dva obrázky znázorňující základní enzymatickou reakci s katalyzátorem a bez něj:
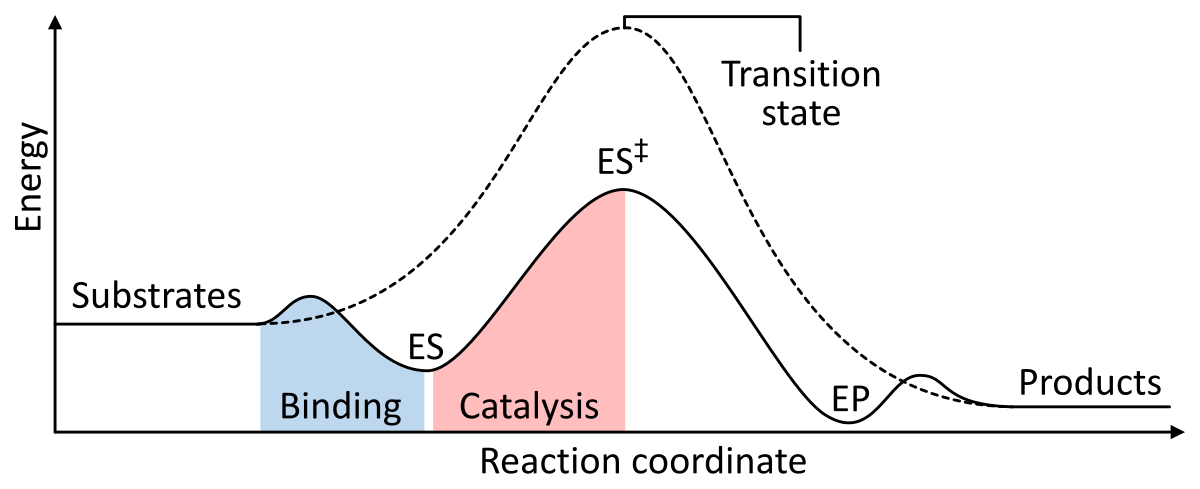
Obrázek 1: Energie jednotlivých fází chemické reakce. Nekatalyzované (čárkovaná čára) substráty potřebují velkou aktivační energii k dosažení přechodného stavu, který se pak rozpadá na produkty s nižší energií. Při enzymové katalýze (plná čára) enzym váže substráty (ES), poté stabilizuje přechodný stav (ES‡), aby se snížila aktivační energie potřebná ke vzniku produktů (EP), které se nakonec uvolní. z Wikipedie.
Účinnost enzymu lze určit takto: uvažujme jednoduchou enzymatickou reakci:
Německý biochemik Leonor Michaelis a kanadská biochemička Maud Mentenová odvodili rovnici popisující tento systém, později známou jako „Michaelis-Mentenova rovnice“, která je uvedena níže:
\}{K_M + } \tag{1}\]
Tato rovnice udává rychlost reakce při dané koncentraci substrátu za předpokladu známé Vmax, což je maximální rychlost, kterou může reakce probíhat, a KM, Michaelisovy konstanty. Při praktickém použití Michaelisovy-Mentenovy rovnice se však často měří V0 a Vmax se pozoruje jako nasycení nebo plošina v grafu dat. Protože je známa koncentrace substrátu, KM je obvykle vypočtená hodnota, která nás zajímá.
Pro \(K_M\) předpokládejte \(V_0= \dfrac{V_{max}}{2}\):
\}{K_M + } \tag{2}\]
\) \dfrac{V_{max}}{2} = V_{max} \tag{3}\]
\ = \dfrac{V_{max}}{\dfrac{V_{max}}{2}} \tag{4} \]
\ = 2 \tag{5}\]
\ \tag{6}\]
Michaelisovu konstantu si lze představit jako rychlost, s jakou se substrát odpoutává od enzymu, což může nastat buď tak, že se komplex substrát-enzym stane produktem, nebo se substrát odpoutá od enzymu. KM lze znázornit jako rovnici.
\
Kde k-1 je rychlostní konstanta, při níž se substrát odváže od enzymu, což vede k disociaci komplexu enzym-substrát, k2 je rychlostní konstanta, při níž komplex substrát-enzym zaniká a mění se v produkt, a K1 je rychlostní konstanta pro vznik komplexu substrát-enzym. Na KM lze tedy pohlížet jako na rychlost zániku komplexu substrát-enzym dělenou rychlostí tvorby komplexu substrát-enzym, což je úroveň, při níž je polovina substrátu vázána na enzym. KM je užitečným indikátorem přítomnosti inhibitoru, protože můžeme sledovat změny KM a porovnávat je s naší kontrolou (biologické systémy, o kterých víme, že v nich inhibitor není přítomen). KM je závisle proměnná a její hodnota se může měnit z mnoha důvodů, včetně úrovně pH systému, teploty nebo jiných podmínek, které mohou ovlivnit chemickou reakci. Malá KM znamená, že substrát má k enzymu vysokou afinitu.
Michaelisova-Mentenova rovnice je nejužitečnější pro měření účinnosti enzymu, pokud se v0 vynese do grafu proti , takto:
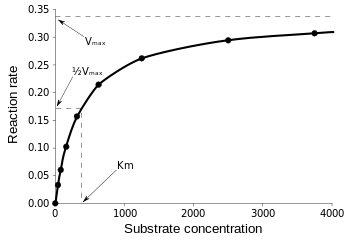
Obrázek 3: Diagram reakční rychlosti a Michaelisovy-Mentenovy konstanty. z Wikipedie.
Vmax je maximální rychlost, kterou může reakce probíhat bez ohledu na , což znamená, že i když přidáte více substrátu, reakce nemůže probíhat rychleji. Je to proto, že při Vmax jsou obsazena všechna aktivní místa na enzymu. Po všech výkladech o různých podobách kinetických rovnic enzymů dojdeme k našemu závěru o katalytické účinnosti. Vrátíme-li se k obr. 3, máme:
\_o}{\dfrac{k_{-1} + k_2}{k_1} + }\right) \tag{8}\]
Všimněte si, že \(k_2\) popisuje nevratnou reakci na rozdíl od rovnovážného vyjádření ve srovnání s k-1 a k1. k2 je zde také znám jako kcat, katalytická účinnost enzymu. Z předchozí diskuse vyplývá, že v0 je naměřená rychlost reakce, což je tvorba produktu v čase, takže lze vyvodit, že rovnice bude vypadat takto:
\}{dt} = k_2_0 \tag{9}\]
Kde 0 je celková koncentrace enzymu.
Je také známo, že VMax nastává, když veškerý komplex enzym-substrát zmizí a změní se na produkty, takže můžeme učinit následující předpoklad:
\_0 \tag{10} \]
a po přeuspořádání máme tuto rovnici:
\_0} \tag{11}\]
To je rovnice pro výpočet katalytické účinnosti, kterou použijeme po získání dat z experimentů a po použití Michaelisovy-Mentenovy rovnice. Při větším kcat je enzym účinný, protože je potřeba méně enzymu
.