Bravais-Gitter

Wissenschaft >Chemie >Festkörper >Bravais-Gitter

In diesem Artikel werden wir die Strukturen der Bravais-Gitter untersuchen.

Ein Kristall ist ein homogener Teil einer festen Substanz, der aus einem regelmäßigen Muster von Struktureinheiten besteht, die durch ebene Flächen verbunden sind, die einen bestimmten Winkel zueinander bilden.

Einheitszelle:

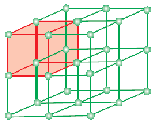
Eine Einheitszelle ist die kleinste strukturelle Wiederholungseinheit eines kristallinen Festkörpers (Raumgitter). Wenn sich Einheitszellen desselben kristallinen Stoffes im Raum in allen Richtungen wiederholen, entsteht ein kristalliner Festkörper. Die Einheitszelle wird auf dem Papier durch Linien dargestellt, die die Zentren der einzelnen Teilchen verbinden.

Die geometrische Form, die nur aus einer regelmäßigen Anordnung von Punkten im Raum besteht, wird als Gitter oder Raumgitter bezeichnet. Es kann als eine Anordnung von Punkten definiert werden, die zeigt, wie Moleküle, Atome oder Ionen an verschiedenen Stellen im dreidimensionalen Raum angeordnet sind. Jeder Punkt am Schnittpunkt der Linien in der Einheitszelle stellt ein Teilchen dar, nämlich ein Molekül, ein Atom oder ein Ion. Dieser Schnittpunkt der Linien in der Einheitszelle wird als Gitterpunkt oder Gitterstelle bezeichnet.

Anmerkung: Jeder Gitterpunkt im Kristallgitter hat die gleiche Umgebung oder Umgebung. Zwei oder mehr kristalline Substanzen können denselben Gitterplatz haben. Jedes einzelne Teilchen in der Anordnung wird immer durch einen Gitterpunkt in der dreidimensionalen Anordnung repräsentiert.

Merkmale des Kristallgitters:

• Das Kristallgitter ist eine regelmäßige Anordnung der Bestandteile eines kristallinen Festkörpers im dreidimensionalen Raum.
• Es besteht aus einer großen Anzahl von Einheitszellen.
• Das Kristallgitter wird durch die Eigenschaften der Einheitszelle definiert.
• Beim Zerfall bildet es zahlreiche Einheitszellen.
• Ein Kristallgitter kann in einem Laboratorium durch Experimente gewonnen, bearbeitet und untersucht werden.
• Es ist eine makroskopische Eigenschaft.

Merkmale der Einheitszelle:

• Eine Einheitszelle ist die kleinste strukturelle Wiederholungseinheit eines kristallinen Festkörpers.
• Es ist die fundamentale Einheit des Kristallgitters, die alle Eigenschaften des Kristalls besitzt.
• Einheitszelle definiert fundamentale Eigenschaften des Kristallgitters.
• Einheitszellen sind eine fundamentale Einheit und können daher nicht weiter unterteilt werden.
• Eine Einheitszelle ist ein hypothetisches Konzept und kann daher nicht durch Experimente erhalten werden.
• Es handelt sich um eine mikroskopische Eigenschaft.

Arten von Raumgittern:

Eindimensionales Gitter:

In diesem Gitter gibt es eine Menge von Punkten, die in gleichen Abständen angeordnet sind.

Zweidimensionales Gitter:

Bei diesem Typ sind zwei Seiten und der Winkel zwischen ihnen angegeben. Es gibt fünf Arten von zweidimensionalen Gittern.

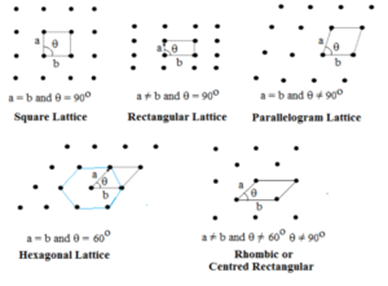
Das sechseckige Gitter ist ein Rhombus mit θ = 60°

Bravais-Gitter:

Lassen Sie die Längen der drei Kanten der Einheitszelle a, b und c sein. Sei α der Winkel zwischen den Seiten b und c. Sei β der Winkel zwischen den Seiten a und c. Sei γ der Winkel zwischen den Seiten a und b.

Der französische Mathematiker Bravais sagte, dass für verschiedene Werte von a, b, c und α, β, γ, maximal vierzehn (14) Strukturen möglich sind. Diese Anordnungen werden Bravais-Gitter genannt.

14 Bravais-Gitter:

Sr. No.	Kristall System	Raumgitter Typ	Diagramm	Kantenlängen	Winkel	Beispiele
	Kubisch	Einfach Primitiv		a = b = c	α = β = γ = 90°	Polonium (Po)
	Kubisch	Körperzentriert		a = b = c	α = β = γ = 90°	Eisen (Fe), Rubidium (Rb), Natrium (Na), Titan (Ti), Wolfram (W), Uran (U), Zirkonium (Zr)
	Kubisch	Flächenzentriert		a = b = c	α = β = γ = 90°	Kupfer (Cu), Aluminium (Al), Nickel (Ni), Gold (Au), Silber (Ag), Platin (Pt)
	Tetragonal	Einfach primitiv		a = b ≠ c	α = β = γ = 90°	SnO2
	Tetragonal	Körper zentriert		a = b ≠ c	α = β = γ = 90°	Ti, O2, CaSO4
	Orthorhombisch	Einfach primitiv		a ≠ b ≠ c	α = β = γ = 90°	Rhombischer Schwefel
	Orthorhombischer	Körper zentriert		a ≠ b ≠ c	α = β = γ = 90°	KNO3
	Orthorhombisch	Fläche zentriert		a ≠ b ≠ c	α = β = γ = 90°	BaSO4
	Orthorhombisch	Ende zentriert		a ≠ b ≠ c	α = β = γ = 90°	MgSO4, 7H2O
	Monoklin	Einfach primitiv		a ≠ b ≠ c	α =γ = 90° und β ≠ 90°	Monokliner Schwefel
	Monoklin	Ende zentriert		a ≠ b ≠ c	α =γ = 90° und β ≠ 90	Na2SO4. 10H2O
	Triclinisch	einfach primitiv		a ≠ b ≠ c	α =γ = 90° und β ≠ 90°	K2Cr2O7, H3BO3
	Hexagonal	Einfach primitiv		a = b ≠ c	α = β = 90° und γ = 120°	ZnO, BeO, CoS, SnS
	Rhomboedrisch	Einfach Primitiv		a ≠ b ≠ c	α = β = γ ≠ 90°	Calcit, NaNO3, FeCO3

Teilchen am Eck:

Das Teilchen an der Ecke der Einheitszelle wird von 8 Einheitszellen geteilt (4 Schichten unten und 4 Schichten oben). Daher ist jede Einheitszelle 1/8 Teilchen.

Teilchen an der Fläche:

Das Teilchen an der Fläche der Einheitszelle wird von 2 benachbarten Einheitszellen geteilt. Daher ist jede Einheitszelle 1/2 Teilchen.

Teilchen am Rand:

Das Teilchen am Rand der Einheitszelle wird von 4 Einheitszellen geteilt (2 Schichten darunter und 2 Schichten darüber). Daher ist jede Einheitszelle 1/4 Teilchen.

Koordinationszahl:

Die Koordinationszahl des konstituierenden Teilchens des Kristallgitters ist die Anzahl der Teilchen, die ein einzelnes Teilchen in einem Kristallgitter umgeben.

Mehr Koordinationszahl bedeutet, dass die Teilchen im Kristallgitter dichter gepackt sind. Die Koordinationszahl ist das Maß für die Härte des Kristalls.

Anzahl der Teilchen in der Einheitszelle und Koordinationszahl

Einfache kubische Struktur (scc):

Aus der Struktur können wir ersehen, dass es 8 Teilchen an 8 Ecken der Einheitszelle gibt.Jedes Eckteilchen wird von 8 benachbarten Einheitszellen geteilt. Jedes Eckteilchen wird von 8 benachbarten Einheitszellen geteilt, so dass jede Einheitszelle 1/8 des Teilchens an ihrer Ecke enthält.
Anzahl der Ecken = 8, daher Anzahl der Teilchen in der Einheitszelle = 1/8x 8 = 1

Jedes Teilchen in dieser Struktur steht in direktem Kontakt mit vier anderen Teilchen in seiner Ebene und je einem Teilchen in der Schicht darüber und in der Schicht darunter. Die Koordinationszahl für die einfache kubische Struktur ist 4+ 1+ 1 = 6

Körperzentrierte kubische Struktur (bcc):

Aus der Struktur können wir ersehen, dass es 8 Teilchen an den 8 Ecken der Einheitszelle gibt.Jedes Eckteilchen wird von 8 benachbarten Einheitszellen geteilt. Somit enthält jede Einheitszelle 1/8 des Teilchens an ihrer Ecke. Anzahl der Ecken = 8, daher Anzahl der Teilchen in der Einheitszelle an den Ecken = 1/8 x 8 = 1

Gleichzeitig befindet sich ein Atom im Zentrum der Zelle, daher die Anzahl der Teilchen in der Einheitszelle 1 + 1 = 2

Jedes Teilchen in dieser Struktur steht in direktem Kontakt mit vier anderen Teilchen in der Schicht darüber und vier Teilchen in der Schicht darunter. Die Koordinationszahl für die körperzentrierte kubische Struktur ist also 4 + 4 = 8

Flächenzentrierte kubische Struktur (fcc):

Aus der Struktur können wir ersehen, dass es 8 Teilchen an 8 Ecken der Einheitszelle gibt. Jedes Eckteilchen wird von 8 anderen benachbarten Einheitszellen geteilt. Somit enthält jede Einheitszelle 1/8 des Teilchens an ihrer Ecke. Die Anzahl der Ecken ist 8. Daher ist die Anzahl der Teilchen in einer Einheitszelle an den Ecken = 1/8 x 8 = 1

Es gibt 6 Teilchen an 6 Flächen der Einheitszelle. Jedes Teilchen einer Fläche wird von 2 benachbarten Einheitszellen geteilt. Daher enthält jede Einheitszelle 1/2 der Teilchen auf ihrer Fläche.
Die Anzahl der Flächen = 6. Daher ist die Anzahl der Teilchen auf der Fläche = 1/2 x 6 = 3

Daher ist die Anzahl der Teilchen in der Einheitszelle 1 + 3 = 4

Jedes Teilchen in dieser Struktur steht in direktem Kontakt mit 4 anderen Teilchen in seiner Schicht und mit 4 Teilchen in der Schicht darüber und 4 Teilchen in der Schicht darunter. Daher ist die Koordinationszahl für die flächenzentrierte kubische Struktur 4 + 4 + 4 = 12

Anmerkungen:

Für das kantenzentrierte Teilchen wird es von 4 Einheitszellen geteilt. Daher besteht jede Einheitszelle aus 1/4 Teilchen. Die Anzahl der Atome pro Einheitszelle steht im gleichen Verhältnis wie die Stöchiometrie der Verbindung. Sie hilft also bei der Vorhersage der Formel der Verbindung.

Wissenschaft > Chemie > Festkörper > Bravais-Gitter