Zentren von Dreiecken

Wo ist das Zentrum eines Dreiecks?

Es gibt tatsächlich Tausende von Zentren!

Hier sind die 4 beliebtesten:

Centroid, Circumcenter, Incenter und Orthocenter

Für jedes dieser Zentren ist das „Zentrum“ dort, wo sich spezielle Linien kreuzen, es hängt also alles von diesen Linien ab!

Schauen wir uns jede dieser Linien an:

Zentroid

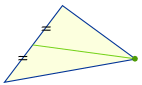Ziehe eine Linie (genannt „Median“) von jeder Ecke zum Mittelpunkt der gegenüberliegenden Seite. Der Schnittpunkt aller drei Linien ist der Schwerpunkt, der auch das „Zentrum der Masse“ ist:

Versuch dies: Schneide ein Dreieck aus Pappe aus, zeichne die Mediane. Treffen sie sich alle in einem Punkt? Kannst du das Dreieck an diesem Punkt ausbalancieren?

Circumcenter

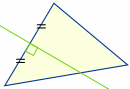Zeichne eine Linie (eine sogenannte „Mittelsenkrechte“) im rechten Winkel zum Mittelpunkt jeder Seite. Der Punkt, an dem sich alle drei Linien schneiden, ist der Mittelpunkt des „Umkreises“ eines Dreiecks, den man „Zirkumzentrum“ nennt:

Versuchen Sie Folgendes: Ziehen Sie die obigen Punkte so lange, bis Sie ein rechtwinkliges Dreieck erhalten (nur nach Augenmaß ist OK). Wo befindet sich der Mittelpunkt des Dreiecks? Und warum?

Umkreismittelpunkt

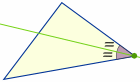Ziehe eine Linie (die sogenannte „Winkelhalbierende“) von einer Ecke aus so, dass sie den Winkel in zwei Hälften teilt Der Punkt, an dem sich alle drei Linien schneiden, ist der Mittelpunkt des „Inkreises“ eines Dreiecks, der „Umkreismittelpunkt“:

Versuch dies: Finde den Mittelpunkt eines Dreiecks mit einem Zirkel und einem Lineal bei: Einzeichnen eines Kreises in ein Dreieck

Ortsmittelpunkt

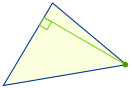Zeichne ein Liniensegment (genannt „Höhe“) im rechten Winkel zu einer Seite, die zur gegenüberliegenden Ecke führt. Der Punkt, an dem sich alle drei Linien schneiden, ist der „orthocenter“:

Beachte, dass manchmal die Kanten des Dreiecks außerhalb des Dreiecks verlängert werden müssen, um die Höhen zu zeichnen. Dann liegt das Orthozentrum ebenfalls außerhalb des Dreiecks.