Fattore di compressibilità (gas) - Knowino

Da Knowino

Questa è una versione controllata di questa pagina

Salta a: navigazione,ricerca

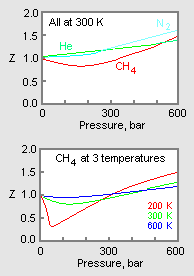
Figura 1: Grafici di esempio dei fattori di compressibilità dei gas

Il fattore di compressibilità (Z) è una proprietà termodinamica utile per modificare la legge dei gas ideali per tenere conto del comportamento dei gas reali. È una misura di quanto le proprietà termodinamiche di un gas reale deviano da quelle previste per un gas ideale. Può essere pensato come il rapporto tra il volume reale di un gas reale e il volume previsto dal gas ideale alla stessa temperatura e pressione del volume reale.

Per un gas ideale, Z ha sempre un valore di 1. Per i gas reali, il valore può deviare positivamente o negativamente, a seconda dell’effetto delle forze intermolecolari del gas. Più un gas reale è vicino al suo punto critico o al suo punto di saturazione, più grandi sono le deviazioni del gas dal comportamento ideale.

Il grafico superiore nella figura 1 illustra come varia il fattore di compressibilità per diversi gas alla stessa temperatura e pressione. Il grafico inferiore illustra come il fattore di compressibilità di un gas (per esempio, il metano) a una data pressione varia con la temperatura.

Questo articolo si occupa solo del fattore di compressibilità dei gas e non approfondisce la compressibilità dei liquidi o delle miscele vapore-liquido.

Contenuti

1 Determinazione dei valori di compressibilità dei gas
- 1.1 Grafici del fattore di compressibilità generalizzato per i gas puri
- 1.2 Grafici del fattore di compressibilità generalizzato per le miscele di gas
- 1.3 L’equazione di van der Waals
  - 1.3.1 Versioni modificate dell’equazione di van der Waals
    - 1.3.1.1 Redlich-Kwong
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
- 1.4 Equazione di stato viriale
- 1.5 Altre equazioni di stato
- 1.6 Notazione per la costante dei gas
2 Riferimenti

Determinazione dei valori di compressibilità dei gas

La legge dei gas ideali è definita come:

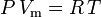
$P\V_mathrm{m} = R\,T$

e la legge dei gas ideali corretta per la non-idealità è definita come:

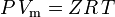
$P\,V_mathrm{m} = ZR\,T$

dove:
P	= pressione
Vm	= volume molare del gas
Z	= fattore di compressibilità
R	= costante universale dei gas
T	= temperatura

e quindi:

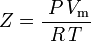
$Z = \frac{\P\,V_\mathrm{m}}{R\T}$

che è l’equazione di stato dei gas reali (EOS) più semplice e più usata. La principale limitazione di questa equazione di stato è che il fattore di compressibilità del gas, Z, non è una costante ma varia da un gas all’altro e con la temperatura e la pressione del gas in esame. Deve essere determinato sperimentalmente.

Qualora siano disponibili dati sperimentali per gas specifici, tali dati possono essere utilizzati per produrre grafici (come nella figura 1) di Z contro la pressione a una temperatura costante o di Z contro la pressione per varie temperature per quei gas specifici. Tali grafici sono utili per ottenere facilmente valori interpolati di Z tra i valori determinati sperimentalmente.

Il fattore di compressibilità, come detto prima, può anche essere espresso come:

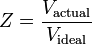
$Z = \frac{V_\mathrm{actual}}{V_\mathrm{ideal}}$

Ci sono tre regimi che influenzano il fattore di compressibilità:

il valore di Z tende a 1 quando la pressione del gas si avvicina a 0, dove tutti i gas tendono al comportamento ideale
il valore di Z è inferiore a 1 a pressioni intermedie perché le forze di attrazione intermolecolari fanno sì che i volumi reali siano inferiori ai valori ideali
il valore di Z è maggiore di 1 e alla fine tende all’infinito alle alte pressioni perché le forze repulsive intermolecolari fanno sì che i volumi reali siano maggiori dei valori ideali

Grafici generalizzati dei fattori di compressibilità per i gas puri

La relazione unica tra il fattore di compressibilità e la temperatura ridotta, Tr, e la pressione ridotta, Pr, è stata riconosciuta per la prima volta da van der Waals nel 1873 ed è conosciuta come il principio dei due parametri degli stati corrispondenti. Il principio degli stati corrispondenti esprime la generalizzazione che le proprietà di un gas che dipendono dalle forze intermolecolari sono legate alle proprietà critiche del gas in modo universale. Ciò fornisce una base importantissima per sviluppare correlazioni di proprietà molecolari.

Per quanto riguarda la compressibilità dei gas, il principio degli stati corrispondenti indica che qualsiasi gas puro alla stessa temperatura ridotta, Tr, e pressione ridotta, Pr, dovrebbe avere lo stesso fattore di compressibilità.

La temperatura e la pressione ridotte sono definite come:

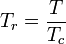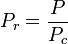
$T_r = \frac{T}{T_c}$ e $P_r = \frac{P}{P_c}$

Tc e Pc sono note come la temperatura critica e la pressione critica di un gas. Sono caratteristiche di ogni gas specifico con Tc che è la temperatura al di sopra della quale non è possibile liquefare un dato gas e Pc è la pressione minima richiesta per liquefare un dato gas alla sua temperatura critica. Insieme definiscono il punto critico di un fluido al di sopra del quale non esistono fasi liquide e gassose distinte di un dato fluido.

I dati di pressione-volume-temperatura (PVT) per i gas reali variano da un gas puro all’altro. Tuttavia, quando i fattori di compressibilità di vari gas monocomponenti sono graficizzati rispetto alla pressione insieme alle isoterme di temperatura (come mostrato per il metano nel grafico inferiore della Figura 1), molti dei grafici mostrano forme di isoterme simili.

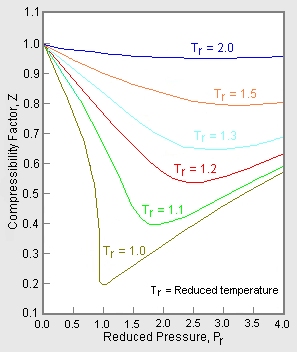
Figura 2: Esempio di un grafico generalizzato del fattore di compressibilità

Per ottenere un grafico generalizzato che può essere usato per molti gas diversi, la pressione e la temperatura ridotta, Pr e Tr, sono usate per normalizzare i dati del fattore di compressibilità. La figura 2 è un esempio di un grafico generalizzato del fattore di compressibilità derivato da centinaia di punti dati sperimentali P-V-T di 10 gas puri, cioè metano, etano, etilene, propano, n-butano, i-pentano, n-esano, azoto, anidride carbonica e vapore.

Esistono grafici più dettagliati dei fattori di compressibilità generalizzati basati su ben 25 o più gas puri diversi, come i grafici di Nelson-Obert. Tali grafici sono detti avere un’accuratezza entro 1-2 per cento per i valori Z maggiori di 0,6 ed entro 4-6 per cento per i valori Z di 0,3-0,6.

I grafici generalizzati del fattore di compressibilità possono essere considerevolmente in errore per i gas fortemente polari che sono gas per i quali i centri di carica positiva e negativa non coincidono. In questi casi la stima di Z può essere in errore anche del 15-20%.

I gas quantici idrogeno, elio e neon non sono conformi al comportamento degli stati corrispondenti e la pressione ridotta e la temperatura per questi tre gas dovrebbero essere ridefiniti nel modo seguente per migliorare la precisione della previsione dei loro fattori di compressibilità quando si usano i grafici generalizzati:

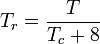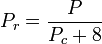
$T_r = \frac{T}{T_c + 8}$ e $P_r = \frac{P}{P_c + 8}$

dove le temperature sono in gradi Kelvin e le pressioni sono in atmosfere.

Grafici del fattore di compressibilità generalizzato per le miscele di gas

I grafici del fattore di compressibilità generalizzato per i gas puri (come esemplificato nella figura 2 o i grafici di Nelson-Obert possono anche essere usati per le miscele di gas usando la regola di Kay proposta da W. B. Kay nel 1936. Questa regola predice il comportamento P-V-T di una miscela di gas determinando il fattore di compressibilità per una miscela di gas a temperatura e pressione ridotte definite in termini di temperatura pseudocritica, Tpc e pressione pseudocritica, Ppc che sono definite come:

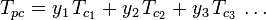
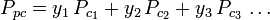
$T_{pc} = y_1\,T_{c_1} + y_2\,T_{c_2} + y_3\,T_{c_3},\punti$ $P_{pc} = y_1\,P_{c_1} + y_2\,P_{c_2} + y_3\,P_{c_3},\punti$

dove:
Tpc	= la temperatura pseudocritica della miscela di gas
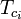$T_{c_i}$	= la temperatura critica di un componente della miscela di gas
Ppc	= la pressione pseudocritica pressione della miscela di gas
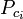$P_{c_i}$	= la temperatura critica di un componente del gas
yi	= la frazione mole (o volume) di un componente del gas

La temperatura pseudoridotta, Tpr, e la pressione pseudoridotta, Ppr, da usare con i grafici del fattore di compressibilità generalizzato per i gas puri sono quindi:

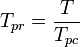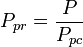
$T_{pr} = \frac{T}{T_{pc}}$ e $P_{pr} = \frac{P}{P_{pc}}$

Su Internet è disponibile un grafico del fattore di compressibilità per il gas naturale (che è una miscela di idrocarburi e altri gas) che utilizza temperature e pressioni pseudoridotte.

L’equazione di van der Waals

L’equazione di van der Waals è stata sviluppata nel 1873 e può essere espressa come:

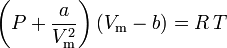
$sinistra(P + \frac{a}{V_mathrm{m}^2}} a destra)\sinistra(V_\mathrm{m} - b a destra) = R\,T$

dove:

a è una misura della forza di attrazione tra le molecole di gas b tiene conto del volume occupato dalle molecole di gas, che diminuisce il volume aperto disponibile

L’equazione di van der Waals può essere riorganizzata come:

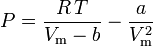
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac {a}{V_\mathrm{m}^2}$

e il fattore di compressibilità può essere scritto come:

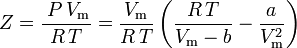
$Z = \frac{;P\,V_mathrm{m}}{R\,T} = \frac{V_mathrm{m}{R\,T} a sinistra(\frac{R\,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2} a destra)$

e ora abbiamo un’equazione per determinare Z usando i parametri a e b di van der Waals:

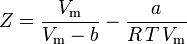
$Z = \frac{V_\mathrm{m}}{V_\mathrm{m} - b} - \frac{a}{R\,T\,V_\mathrm{m}}$

Anche se a e b sono indicati come “le costanti di Van der Waals”, non sono veramente costanti perché variano da un gas all’altro; sono, comunque, indipendenti da P, V e T. In altre parole, sono costanti per il gas considerato. Date la temperatura e la pressione critiche per un gas specifico, a e b possono essere ottenute per quel gas specifico da queste equazioni:

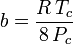
$a = \frac{27\, R^2\, T_c^2}{64\, P_c}$ e $b = \frac{R\, T_c}{8\, P_c}$

Ad esempio, la pressione critica dell’etano è 4.884 MPa e la temperatura critica è 305,43 K (32,3˚C). Usando la costante universale dei gas, R, di 8,3145 Pa m3 K-1 mol-1, le equazioni di cui sopra producono a = 0,557 m6 Pa mol-2 e b = 6,500×10-5 m3 mol-1.

I valori tabulati di a e b per vari gas sono disponibili in questi riferimenti e in molte altre fonti della letteratura tecnica.

Versioni modificate dell’equazione di van der Waals

La determinazione dei fattori di compressibilità usando l’equazione di stato di van der Waals è un miglioramento rispetto all’uso delle tabelle di compressibilità generalizzate. Tuttavia, ci sono versioni modificate dell’equazione di stato di van der Waals che forniscono un miglioramento ancora maggiore. Forse le equazioni di stato più comunemente usate dagli ingegneri che lavorano nella raffinazione del petrolio, nella produzione petrolchimica, nel trattamento del gas naturale, nella distillazione criogenica e nelle industrie correlate sono: l’equazione Redlich-Kwong sviluppata nel 1949, l’equazione Soave-Redlich-Kwong sviluppata nel 1972 e l’equazione Peng-Robinson sviluppata nel 1976. Queste tre equazioni sono essenzialmente versioni modificate dell’equazione di van der Waals. Le equazioni comparative sono:

Redlich-Kwong

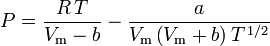
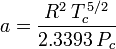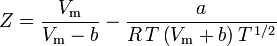
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}left(V_\mathrm {m} + b\right)T^{\mathrm,1/2}$ $a = \frac{R^2\, T_c^{\mathrm,5/2}{2.3393\, P_c}$ e $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_mathrm{m}}{V_mathrm{m} - b} - \frac{a}{R\, T\left(V_mathrm {m} + b\right)T^{\,1/2}$

Soave-Redlich-Kwong

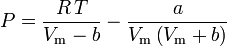
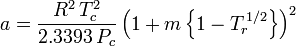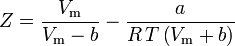
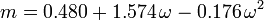
$P = \frac{R\,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m} a sinistra(V_\mathrm {m} + b\right)}$ $a = \frac{R^2\,T_c^2}{2.3393\,P_c}, \Big(1 + m\, \Big\{1 - T_r^{\ 1/2} \Big\} \Big)^2$ e $b = \frac{R\, T_c}{11.5420\, P_c}$ $Z = \frac{V_mathrm{m}}{V_mathrm{m} - b} - \frac{a}{R\, T\left(V_mathrm {m} + b\destra)}$ $m = 0.480 + 1.574\, \omega - 0.176\, \omega^2$

Il fattore acentrico, ω, usato come parametro nelle equazioni di Soave-Redlich-Kwong e Peng-Robinson fu introdotto per la prima volta da Pitzer et al nel 1955. Può essere espresso come:

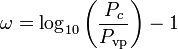
$omega = \log_{10} \sinistra(\frac{P_c}{P_mathrm{vp}}}destra) - 1$

dove Pvp è la pressione di vapore satura del gas ad una temperatura di 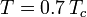$T = 0.7\, T_c$ .

Peng-Robinson

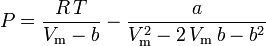
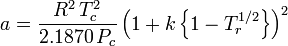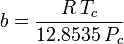
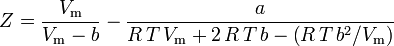
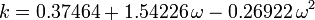
$P = \frac{R,T}{V_\mathrm{m} - b} - \frac{a}{V_\mathrm{m}^2 - 2\,V_\mathrm{m}, b - b^2}$ $a = \frac{R^2\,T_c^2}{2.1870\,P_c}, \Big(1 + k\, \Big\{1 - T_r^{1/2} \Big\} \Big)^2$ e $b = \frac{R\, T_c}{12.8535\, P_c}$ $Z = \frac{V_mathrm{m}{V_mathrm{m} - b} - \frac{a}{R\,T\,V_mathrm{m} + 2\R,R\T\,b - \sinistra(R\T\, b^2/V_mathrm{m}destra)}$ $k = 0,37464 + 1,54226\, \omega - 0,26922\, \omega^2$

Equazione di stato viriale

L’equazione di stato più fondamentale, in quanto ha il fondamento teorico più solido, è l’equazione di stato viriale:

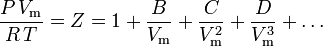
$frac{P\P\,V_mathrm{m}{R\T} = Z = 1 + \frac{B}{V_mathrm{m} + \frac{C}{V_mathrm{m}^2} + \frac{D}{V_mathrm{m}^3} \punti$

È stato proposto per la prima volta su base empirica da Thiesen nel 1885 e ulteriormente sviluppato nel 1901 da Kamerlingh-Onnes. Un’espressione statistico-meccanica per B fu derivata per la prima volta da Ornstein nella sua tesi di dottorato. L’equazione fu successivamente sviluppata nuovamente da H.D. Ursell nel 1927 su una base teorica derivata da un’analisi statistico-meccanica (cluster) delle forze intermolecolari.

I parametri B, C e D sono indicati come il secondo, terzo e quarto coefficiente viriale, rispettivamente. I coefficienti non sono costanti poiché variano da un gas all’altro così come la temperatura del gas in esame. A volte sono scritti come B(T), C(T) e D(T) per indicare che sono funzioni della temperatura. Il valore numerico dei coefficienti deve essere determinato sperimentalmente.

Il secondo coefficiente viriale fornisce la maggior parte della correzione per il comportamento non ideale di un gas. Per questo motivo, l’equazione viriale è talvolta troncata dopo il termine contenente il secondo coefficiente. Tuttavia, quando il terzo coefficiente è disponibile, l’equazione è solitamente troncata dopo il termine contenente il terzo coefficiente. Il quarto coefficiente è raramente disponibile.

Un’ampia compilazione di coefficienti viriali per gas puri e miscele di gas è stata preparata dal database dei coefficienti viriali presso il Thermodynamics Research Center, precedentemente presso la Texas A&M University, College Station, Texas e ora situato presso il National Institute of Standards and Technology (NIST), Boulder, Colorado. L’ultima versione di questa compilazione è stata pubblicata nel 2003. Il NIST offre anche per l’acquisto un programma software, NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP), che include i coefficienti di secondo e terzo viriale così come una serie di altre proprietà termodinamiche.

Altre equazioni di stato

Ci sono una serie di altre equazioni di stato per prevedere il comportamento dei gas reali. Forse, le più note sono l’equazione Beattie-Bridgeman sviluppata nel 1929 e l’equazione Benedict-Rubin-Webb sviluppata nel 1940. In generale, sono più complesse delle equazioni discusse sopra.

Notazione per la costante dei gas

La costante dei gas usata in questo articolo è la costante dei gas universale, R, che si applica a qualsiasi gas. C’è anche una costante dei gas specifica, che può essere indicata come Rs, ed è definita come Rs = R / M dove M è il peso molecolare.

Purtroppo, molti autori nella letteratura tecnica a volte usano R come costante specifica dei gas senza denotarla come tale o dichiarare che è la costante specifica dei gas. Questo può e porta a confusione.

1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. e Simon, John D. (1999). Termodinamica molecolare. University Science Books. ISBN 1-891389-05-X.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal e Robert H. Turner (2004). Fondamenti di scienze termo-fluidiche, 2a edizione. McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M. et al. (2005). Introduzione alla termodinamica dell’ingegneria chimica, settima edizione. McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). Termodinamica dell’ingegneria chimica. Universities Press (India). ISBN 81-7371-048-1.
5.0 5.1 Leggi dei gas (Conferenza del Professor M.J. Mombourquette alla Queens University, Canada)
Hong Wei Xiang (2005). Il principio degli stati corrispondenti e la sua pratica: Proprietà termodinamiche, di trasporto e di superficie dei fluidi. Elsevier. ISBN 0-444-52062-7.
Goldbook IUPAC
Gouq-Jen Su (1946). “Legge modificata degli stati corrispondenti”. Industrial & Engineering Chemistry 38 (8): 803-806. ISSN 0096-4484.
9.0 9.1 Equazioni di stato (Professor Lyes Kadem, Concordia University, Canada)
10.0 10.1 Equazioni di stato (materiale di lezione usato dal Professor Sanford Klein all’Università del Wisconsin-Madison, USA)
Richard W. Miller (1996). Flow Measurement Engineering Handbook, 3a edizione. McGraw-Hill. ISBN 0-07-042366-0. (Vedi Figura G-1 a pagina G.145)
Kai-Fui Vincent Wong (2000). Termodinamica per gli ingegneri, 1a edizione. CRC Press. ISBN 0-8493-0232-3. (Vedi Figura A-2, pagina 278}
Grafici di compressibilità generalizzata Nelson-Obert (Grafici disponibili su Internet, dal sito web della San Diego State University, USA)
W.B.Kay (1936). “Gas e vapori ad alta temperatura e pressione – Densità degli idrocarburi”. Ingegneria industriale & Chimica 28:1014. ISSN 0096-4484.
Yunus A. Çengal e Michael A. Bowes (2005). Termodinamica: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (materiale di lezione usato dal Professor R.M. Price alla Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). Manuale di chimica e fisica, 56a edizione. CRC Press. ISBN 0-87819-455-X.
19.0 19.1 19.2 Capitolo 3: Equazioni di stato (pagine 6-8 di 65 pagine pdf) (Parte della tesi di dottorato di Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
20.0 20.1 20.2 Jean Vidal (2003). Termodinamica: Applicazioni nell’ingegneria chimica e nell’industria petrolifera. Edizioni Technip. ISBN 2-7108-0800-5.
Zakia Nasri e Housam Binous (2007). “Applicazioni dell’equazione di stato Soave-Redlich-Kwong usando Mathematica”. Giornale di Ingegneria Chimica del Giappone 40 (6): 534-538. Recuperato da qui.
K.S. Pitzer et al (1955). “Le proprietà volumetriche e termodinamiche dei fluidi”. Journal of the American Chemical Society 77: 3427-3440.
Francis S. Manning e Richard E. Thompson (1991). Oilfield Processing of Petroleum. Pennwell Books. ISBN 0-87814-343-2.
Definizione del fattore acentrico (Physical Property Sources Index, PPSI, del Politecnico federale di Zurigo)
Max F. Thiesen (1885). “Indagini sull’equazione di stato”. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901). “Espressione dell’equazione di stato dei gas e dei liquidi per mezzo di serie”. Commun. Laboratorio di Fisica. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Applicazione della meccanica statistica di Gibbs su problemi di teoria molecolare), Leiden
H. D. Ursell (1927). “La valutazione dell’integrale di fase di Gibbs per i gas imperfetti” (23): 685.
J.D. Dymond e R.C. Wilhoit (Autori), K.N. Marsch e M. Fenkel (Editori) (2003). Coefficienti Viriali dei gas puri e delle miscele, 1a Edizione. Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie e O.C. Bridgeman (1929). “Una nuova equazione di stato per i fluidi”. Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb e L.C. Rubin (1940). “Un’equazione empirica per le proprietà termodinamiche degli idrocarburi leggeri e delle loro miscele”. J. Chem. Phys. 8: 334-335.

Alcuni contenuti di questa pagina potrebbero essere precedentemente apparsi su Citizendium.

Recuperato da “http://knowino.org/wiki/Compressibility_factor_(gases)”

Categoria: Fisica