Centres des triangles

Où se trouve le centre d’un triangle ?

Il existe en fait des milliers de centres !

Voici les 4 plus populaires :

Centroïde, Circumcentre, Incentre et Orthocentre

Pour chacun d’eux, le « centre » est l’endroit où se croisent des lignes spéciales, donc tout dépend de ces lignes !

Regardons chacun d’eux :

Centroïde

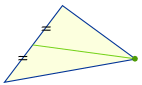Dessinez une ligne (appelée « médiane ») de chaque coin au point médian du côté opposé. L’endroit où les trois lignes se croisent est le centroïde, qui est aussi le « centre de masse » :

Essayez ceci : découpez un triangle dans du carton, tracez les médianes. Se rejoignent-elles toutes en un point ? Pouvez-vous équilibrer le triangle en ce point ?

Circumcenter

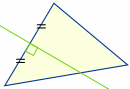Dessinez une ligne (appelée « bissectrice perpendiculaire ») à angle droit avec le point médian de chaque côté. L’endroit où les trois lignes se croisent est le centre de la « circonférence » d’un triangle, appelé « centre circonférentiel »:

Essayez ceci : faites glisser les points ci-dessus jusqu’à ce que vous obteniez un triangle rectangle (juste à l’œil est OK). Où se trouve le centre de gravité ? Pourquoi ?

Incentre

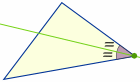Tracez une ligne (appelée « bissectrice d’angle ») à partir d’un angle de façon à ce qu’elle divise l’angle en deux L’endroit où les trois lignes se croisent est le centre de « l’incercle » d’un triangle, appelé « incentre » :

Essayez : trouvez l’incentre d’un triangle en utilisant un compas et une règle à.. : Inscrire un cercle dans un triangle

Orthocentre

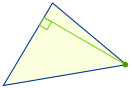Tracer un segment de droite (appelé « altitude ») à angle droit avec un côté qui va vers le coin opposé. L’endroit où les trois lignes se croisent est l' »orthocentre »:

Notez que parfois les bords du triangle doivent être prolongés à l’extérieur du triangle pour dessiner les altitudes. Alors l’orthocentre est aussi à l’extérieur du triangle.