Una matrice di confusione è una tabella che viene spesso utilizzata per descrivere le prestazioni di un modello di classificazione (o “classificatore”) su un insieme di dati di test per i quali sono noti i valori veri. La matrice di confusione in sé è relativamente semplice da capire, ma la relativa terminologia può confondere.
Ho voluto creare una “guida di riferimento rapido” per la terminologia della matrice di confusione perché non sono riuscito a trovare una risorsa esistente che soddisfacesse i miei requisiti: una presentazione compatta, usando numeri invece di variabili arbitrarie, e spiegata sia in termini di formule che di frasi.
Iniziamo con un esempio di matrice di confusione per un classificatore binario (anche se può essere facilmente esteso al caso di più di due classi):
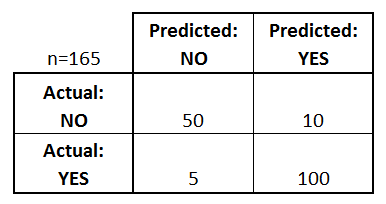
Cosa possiamo imparare da questa matrice?
- Ci sono due possibili classi previste: “sì” e “no”. Se stessimo predicendo la presenza di una malattia, per esempio, “sì” significherebbe che hanno la malattia, e “no” significherebbe che non hanno la malattia.
- Il classificatore ha fatto un totale di 165 previsioni (es, 165 pazienti sono stati testati per la presenza di quella malattia).
- Di questi 165 casi, il classificatore ha predetto “sì” 110 volte, e “no” 55 volte.
- In realtà, 105 pazienti nel campione hanno la malattia, e 60 pazienti no.
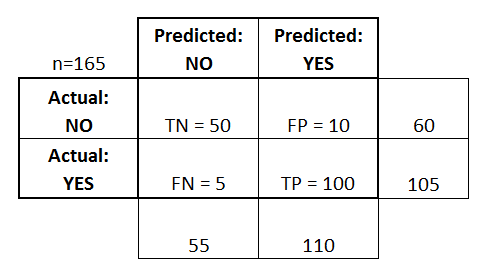
Definiamo ora i termini più fondamentali, che sono numeri interi (non tassi):
- veri positivi (TP): Questi sono casi in cui abbiamo predetto sì (hanno la malattia), e hanno la malattia.
- veri negativi (TN): Abbiamo predetto di no, e non hanno la malattia.
- falsi positivi (FP): Abbiamo predetto di sì, ma in realtà non hanno la malattia. (Conosciuto anche come “errore di tipo I”.)
- falsi negativi (FN): Abbiamo predetto di no, ma in realtà hanno la malattia. (Conosciuto anche come “errore di tipo II”)
Ho aggiunto questi termini alla matrice di confusione, e ho anche aggiunto i totali di riga e colonna:
Questa è una lista di tassi che sono spesso calcolati da una matrice di confusione per un classificatore binario:
- Accuratezza: Complessivamente, quanto spesso il classificatore è corretto?
- (TP+TN)/totale = (100+50)/165 = 0,91
- (FP+FN)/totale = (10+5)/165 = 0,09
- equivalente a 1 meno la precisione
- conosciuto anche come “tasso di errore”
- TP/sì effettivo = 100/105 = 0,95
- conosciuto anche come “Sensibilità” o “Recall”
- FP/attuale no = 10/60 = 0,17
- TN/attuale no = 50/60 = 0,83
- equivalente a 1 meno il False Positive Rate
- anche conosciuto come “Specificità”
- TP/predetto sì = 100/110 = 0,91
Vanno menzionati anche un paio di altri termini:
- Tasso di errore nullo: Questo è quanto spesso vi sbagliereste se prevedeste sempre la classe di maggioranza. (Nel nostro esempio, il tasso di errore nullo sarebbe 60/165=0,36 perché se tu predicessi sempre sì, avresti sbagliato solo per i 60 casi “no”). Questa può essere un’utile metrica di base con cui confrontare il vostro classificatore. Tuttavia, il miglior classificatore per una particolare applicazione a volte avrà un tasso di errore più alto del tasso di errore nullo, come dimostrato dal paradosso della precisione.
- Kappa di Cohen: Questa è essenzialmente una misura di quanto bene il classificatore ha eseguito rispetto a quanto bene avrebbe eseguito semplicemente per caso. In altre parole, un modello avrà un alto punteggio Kappa se c’è una grande differenza tra l’accuratezza e il tasso di errore nullo. (Maggiori dettagli sul Kappa di Cohen.)
- Punteggio F: Questa è una media ponderata del tasso di vero positivo (recall) e della precisione. (Maggiori dettagli sul punteggio F.)
- Curva ROC: Questo è un grafico comunemente usato che riassume le prestazioni di un classificatore su tutte le possibili soglie. Viene generato tracciando il tasso di vero positivo (asse y) contro il tasso di falso positivo (asse x) al variare della soglia di assegnazione delle osservazioni a una data classe. (Maggiori dettagli sulle curve ROC.)
E infine, per quelli di voi provenienti dal mondo della statistica bayesiana, ecco un rapido riassunto di questi termini da Applied Predictive Modeling:
In relazione alla statistica bayesiana, la sensibilità e la specificità sono le probabilità condizionali, la prevalenza è il priore, e i valori positivi/negativi previsti sono le probabilità posteriori.
Vuoi saperne di più?
Nel mio nuovo video di 35 minuti, Making sense of the confusion matrix, spiego questi concetti in modo più approfondito e copro argomenti più avanzati:
- Come calcolare precisione e richiamo per problemi multiclasse
- Come analizzare una matrice di confusione a 10 classi
- Come scegliere la giusta metrica di valutazione per il tuo problema
- Perché la precisione è spesso una metrica fuorviante
Fammi sapere se hai delle domande!