Tudomány > Kémia > Szilárdtestek > Bravais rácsok
Ebben a cikkben a Bravais rácsok szerkezetét fogjuk tanulmányozni.
A kristály egy szilárd anyag homogén része, amely az egymással meghatározott szöget bezáró síkfelületek által kötött szerkezeti egységek szabályos mintázatából áll.
Egységcella:
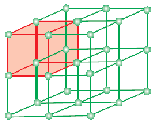
Az egységcella a kristályos szilárd anyag legkisebb szerkezeti ismétlődő egysége (térrács). Ha ugyanannak a kristályos anyagnak az egységcellái a térben minden irányban ismétlődnek, akkor kristályos szilárd anyag jön létre. Az egységcellát papíron az alkotórészecskék középpontjait összekötő vonalak rajzolásával ábrázoljuk.
A csak pontok szabályos térbeli elrendezéséből álló geometriai formát rácsnak vagy térrácsnak nevezzük. Ez pontok olyan tömbjeként definiálható, amely megmutatja, hogy a molekulák, atomok vagy ionok hogyan helyezkednek el különböző helyeken, háromdimenziós térben. Az egységcellában lévő vonalak metszéspontjában minden egyes pont alkotó részecskét, azaz molekulát, atomot vagy iont jelöl. Az egységcellában a vonalak metszéspontját rácspontnak vagy rácshelynek nevezzük.
Megjegyzés: A kristályrácsban minden rácspontnak ugyanaz a környezete vagy környezete. Két vagy több kristályos anyagnak is lehet ugyanolyan rácshelye. A tömb minden egyes részecskéje mindig egy rácspontot képvisel a háromdimenziós tömbben.
A kristályrács jellemzői:
- A kristályrács egy kristályos szilárd anyag alkotórészecskéinek szabályos elrendeződése a háromdimenziós térben.
- Nagyszámú egységcellából áll.
- A kristályrácsot az egységcellák tulajdonságai alapján határozzuk meg.
- Töréskor számos egységcellát alkot.
- A kristályrácsot laboratóriumban, kísérletek során lehet előállítani, kezelni és tanulmányozni.
- Ez egy makroszkopikus tulajdonság.
Az egységcella jellemzői:
- Az egységcella a kristályos szilárd anyag legkisebb szerkezeti ismétlődő egysége.
- A kristályrács alapvető egysége, amely a kristály minden tulajdonságával rendelkezik.
- Az egységcella meghatározza a kristályrács alapvető tulajdonságait.
- Az egységcella alapvető egység, ezért nem osztható tovább.
- Az egységcella hipotetikus fogalom Ezért a kísérletek során nem kapható.
- Ez egy mikroszkopikus tulajdonság.
Térrácsok típusai:
Egydimenziós rács:
Ebben a rácsban egyenlő távolságban elhelyezett pontok halmaza létezik.

Kétdimenziós rács:
Ebben a típusban két oldal és a köztük lévő szög van megadva. A kétdimenziós rácsnak öt típusa van.
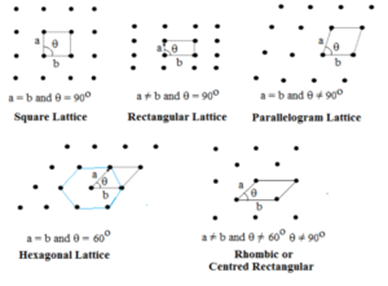
A hexagonális rács egy rombusz, amelynek θ = 60°
Bravais rácsok:

Legyen az egységcella három élének hossza a, b és c. Legyen α a b és c oldal közötti szög. β legyen az a és c oldal közötti szög. γ legyen az a és b oldal közötti szög.
A francia matematikus Bravais szerint a, b, c és α, β, γ különböző értékei esetén legfeljebb tizennégy (14) szerkezet lehetséges. Ezeket az elrendezéseket Bravais rácsoknak nevezik.
14 Bravais rács:
|
Sr. No. |
Kristály Rendszer |
Térrács Típus |
Diagram |
Sarkok hossza |
Szögek |
Példák |
|
Kubikus |
Simple primitív |
 |
a = b = c |
α = β = γ = 90° |
Polonium (Po) |
|
|
Kocka |
Testközpontú |
 |
a = b = c |
α = β = γ = 90° |
A vas (Fe), Rubídium (Rb), Nátrium (Na), Titán (Ti), Volfram (W), Urán (U), Cirkónium (Zr) |
|
|
Cubic |
Face centred |
 |
a = b = c |
α = β = γ = 90° |
Réz (Cu), Alumínium (Al), Nikkel (Ni), arany (Au), ezüst (Ag), Platina (Pt) |
|
|
Tetragonális |
egyszerű . primitív |
 |
a = b ≠ c |
α = β = γ = 90° |
SnO2 |
|
|
Tetragonális |
test. centrikus |
 |
a = b ≠ c |
α = β = γ = 90° |
Ti, O2, CaSO4 |
|
|
Orthorombikus |
Simple primitív |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
Rhombikus kén |
|
|
Orthorhombikus |
test. centrikus |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
KNO3 |
|
|
Orthorombikus |
Face centrikus |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
BaSO4 |
|
|
Orthorombikus |
End centrikus |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
MgSO4, 7H2O |
|
|
Monoklin |
egyszerű . primitív |
 |
a ≠ b ≠ c |
α =γ = 90° és β ≠ 90° |
Monoklin kén |
|
|
Monoklin |
End centrikus |
 |
a ≠ b ≠ c |
α =γ = 90° és β ≠ 90 |
Na2SO4. 10H2O |
|
|
Triklin |
egyszerű primitív |
 |
a ≠ b ≠ c |
α =γ = 90° és β ≠ 90° |
K2Cr2O7, H3BO3 |
|
|
Exagonális |
egyszerű primitív |
 |
a = b ≠ c |
α = β = 90° és γ = 120° |
ZnO, BeO, CoS, SnS |
|
|
Rhomboéder |
Simple primitív . |
 |
a ≠ b ≠ c |
α = β = γ ≠ 90° |
Kalcit, NaNO3, FeCO3 |
Részecske a sarokban:

A részecske az egységcella sarkán 8 egységcellán osztozik (4 réteg alatt és 4 réteg felett). Ezért minden egyes egységcella 1/8 részecske.
Részecske az arcnál:

Az egységcella arcánál lévő részecskén 2 szomszédos egységcella osztozik. Ezért minden egységcella 1/2 részecske.
Részecske az élen:

A részecskét az egységcella szélén 4 egységcella osztja meg (2 réteg alatt és2 réteg felett). Ezért minden egyes egységcella 1/4 részecske.
Koordinációs szám:
A kristályrács alkotórészecskéjének koordinációs száma a kristályrácsban egyetlen részecskét körülvevő részecskék száma.
Mennél nagyobb a koordinációs szám, annál sűrűbben vannak a részecskék a kristályrácsban elhelyezve. A koordinációs szám a kristály keménységének a mértéke.
A részecskék száma az egységcellában és a koordinációs szám
egyszerű kubikus szerkezet (scc):

A szerkezetből látható, hogy az egységcella 8 sarkában 8 részecske van.Minden sarokrészecskén 8 szomszédos egységcella osztozik. Ezért minden egyes egységcellában 1/8 részecske van a sarkában.
Sarkok száma = 8, Ezért a részecskék száma az egységcellában = 1/8x 8 = 1
Minden részecske ebben a szerkezetben közvetlenül érintkezik négy másik részecskével a síkjában és egy-egy részecskével a felette és az alatta lévő rétegben. Hencethe koordinációs szám az egyszerű köbös szerkezetre 4+ 1+ 1 = 6

Testközpontú köbös szerkezet (bcc):

A szerkezetből látható, hogy az egységcella 8 sarkában 8 részecske van.Minden sarokrészecske 8 szomszédos egységcellán osztozik. Ezért minden egyes egységcella 1/8-od részecskét tartalmaz a sarkán. A sarkok száma = 8,ezért a sarkokban lévő részecskék száma az egységcellában = 1/8 x 8 = 1
Az egységcella közepén ugyanakkor egy atom van, Ezért a részecskék száma az egységcellában 1 + 1 = 2
A szerkezetben minden részecske közvetlenül érintkezik négy másik részecskével a fenti rétegben és négy részecskével az alsó rétegben. Ezért a koordinációs szám a testközpontú köbös szerkezetnél 4 + 4 = 8

FaceCentered Cubic Structure (fcc):

A szerkezetből látható, hogy az egységcella 8 sarkában 8 részecske van. Minden sarokrészecske 8 másik szomszédos egységcellán osztozik. Ezért minden egyes egységcella 1/8-od részecskét tartalmaz a sarkában. A sarkok száma = 8. Ezért az egységcellában a sarkoknál lévő részecskék száma = 1/8 x 8 = 1
Az egységcella 6 felületén 6 részecske van. Minden felület részecskéjén 2szomszédos egységcella osztozik. Ezért minden egyes egységcella 1/2 részecskét tartalmaz az arcán.
Az arcok száma = 6. Ezért az arcokon lévő részecskék száma = 1/2 x 6 = 3
Az egységcellában lévő részecskék száma 1 + 3 = 4
Minden részecske ebben a szerkezetben közvetlenül érintkezik 4 másik részecskével a saját rétegében, valamint 4 részecskével a felette lévő rétegben és4 részecskével az alatta lévő rétegben. Ezért a koordinációs szám az élközpontú köbös szerkezet esetében 4 + 4 + 4 = 12

Megjegyzések:
Az élközpontú részecske esetében 4 egységcellán osztozik. Ezért minden egyes egységcella 1/4 részecskéből áll Az atomok száma egységcellánként a vegyület sztöchiometriájával megegyező arányban van. Ezért segít megjósolni a vegyület képletét.
Tudományok > Kémia > Szilárdtestek > Bravais rácsok