バリセントリック座標

by
幾何学 > CoordinateGeometry >
Geometry > Plane Geometry > Triangle > Triangle Properties >

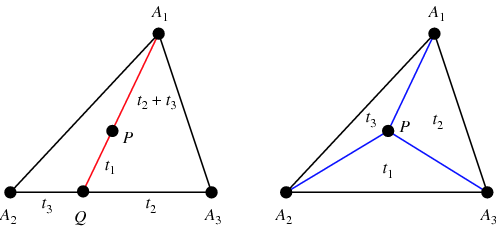
Barycentric coordinates are triple of number (t_1),t_2,t_3)は、基準三角形DeltaA_1A_2A_3の頂点に置かれた質点に対応する。 これらの質量は次に点Pを決定し、それは3つの質量の幾何学的重心であり、座標（t_1,t_2,t_3）と同定される。 三角形の頂点は (1,0,0), (0,1,0), (0,0,1) で示される。 バリセントリック座標は1827年にメビウスが発見した（Coxeter 1969, p.217; Fauvel et al.1993）。 Barycentric

任意の点Pのバリセントリック座標を求めるには、直線A_1Pと辺A_2A_3との交点Qからt_2、t_3と求める。 で、Qにある質量t_2+t_3と釣り合うA_1の質量をt_1とし、Pを重心とする（左図参照）。 さらに三角形 DeltaA_1A_2P, DeltaA_1A_3P, DeltaA_2A_3P の面積は P のバリセントリック座標 t_3, t_2, t_1 と比例する (右図; Coxeter 1969, p. 217).

バリセントリック座標は同次なので

(t_1,t_2,t_3)=(mut_1,mut_2,mut_3)
(1)

for mu!=0.

副三角形の実際の面積になるように正規化したバリセントリック座標をホモジニアス・バリセントリック座標という。

t_1+t_2+t_3=1,
(2)

そうすると元の三角形の面積で正規化した部分三角形の面積となるので、これを面積座標という（Coxeter 1969, p. 218)。 バリセントリック座標と面座標は、Routhの定理、Cevaの定理、Menelausの定理などの幾何学的定理の特にエレガントな証明を提供できる（Coxeter 1969, pp.219-221）

（必ずしも均質ではない）多くの共通中心に対するバリセントリック座標を次の表にまとめた。 表中、a、b、cは三角形の辺の長さ、sはその半周期である。

三角形の中心 バリセントリック座標
円心O (a^2(b^2+c^2-a^2), b^2(c^2+a^2-b^2), c^2(a^2+b^2-c^2))
excenter J_A (-a.-)(-a,b,c)
エキセンタ J_B (a,-b,c)
エキセンタ J_C (a,b,-c)
Gergonne 点 Ge ((s-b)(s-c), (s-c)(s-a))． (s-a)(s-b))
インセンタ I (a,b,c)
Nagel point Na (s-a,s-b,s-c)
orthocenter H ((a^2+b^2-c^2)(c^2+a^2-b^2), (b^2+c^2-a^2)(a^2+b^2-c^2), (c^2+a^2-b^2)(b^2+c^2-a^2))
symmedian point K （a^2,b^2,c^2)
三角形のセントロイド G (1,1,1)

バリセントリック座標において、直線は線形同次方程式を持つ。 特に点(r_1,r_2,r_3)と(s_1,s_2,s_3)を結ぶ線は方程式

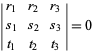|r_1 r_2 r_3 を有する。 s_1 s_2 s_3; t_1 t_2 t_3|=0
(3)

(Loney 1962, pp. 39 and 57; Coxeter 1969, p. 219; Bottema 1982)。 三角形DeltaP_1P_2P_3の頂点P_iがバリセントリック座標(x_i,y_i,z_i)であれば、その面積は

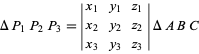DeltaP_1P_2P_3=|x_1 y_1 z_1; x_2 y_2 z_2; x_3 y_3 z_3|DeltaABC
(4)

(Bottema 1982, Yiu 2000) となる。

コメントする