圧縮率（気体）

From Knowino

へジャンプすることができます。 navigation,search

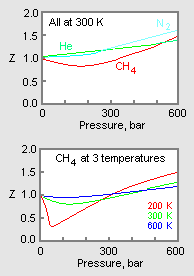
Figure 1: ガス圧縮率のグラフ例

圧縮率（Z）は理想気体の法則を修正して、実際の気体の挙動を説明するのに都合のよい熱力学的性質である。これは実際の気体の熱力学的性質が理想気体で予想される性質からどの程度ずれているかを示す指標である。理想気体の体積と同じ温度と圧力で予測される体積に対する実際の気体の体積の比と考えることができる。

理想気体の場合、Zの値は常に1であるが、実際の気体の場合、気体の分子間力の影響により正または負にずれることがある。図1の上のグラフは、同じ温度と圧力で、異なる気体の圧縮率がどのように変化するかを示したもので、圧縮率が大きいほど理想的な挙動を示す。

本稿では気体の圧縮率のみを扱い、液体や気液混合物の圧縮率には踏み込まない。

1 気体圧縮率の値を決定するには。1 純ガスの一般化圧縮率グラフ
1.2 混合ガスの一般化圧縮率グラフ
1.3 van der Waals 式
- 1.3.1 van der Waals式の修正版
  - 1.3.1 混合ガスの一般化圧縮率グラフ
  - 1.2 混合ガスの一般化圧縮率グラフ
  - 1.3 van der Waals式
    - 1.1 純ガスの一般化圧縮率グラフ
    - 1.3.1.2 Soave-Redlich-Kwong
    - 1.3.1.3 Peng-Robinson
    1.4 Virial equation of state
  - 1.5 その他の状態方程式
  - 1.3.3 状態方程式
- 1.4 状態方程式
- 1.3.2 状態方程式
- 1.4 状態方程式
- 1.1.1 状態方程式
2 参考文献

気体の圧縮率値の決定

理想気体の法則は次のように定義されている。

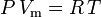
$Penta,V_mathrm{m} = Renta,T$

そして非理想性を補正した理想気体の法則は次のように定義される：

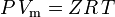
$Penta,V_mathrm{m} = ZR,T$

そこで。
P	= 圧力
Vm	= 気体のモル体積
Z	= 圧縮率
R	=普遍気体定数
T	=温度

となり、こうなる。

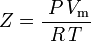
$Z = \frac{P;V_mathrm}}{R,T}$

これは最も簡単で広く使われている気体の状態方程式である。この状態方程式の大きな欠点は、気体の圧縮率Zが定数ではなく、気体ごとに、また対象とする気体の温度や圧力によって変化することである。これは実験的に決定されなければならない。

特定のガスについての実験データが利用可能である場合、そのデータは、それらの特定のガスについての一定温度での圧力に対するZまたは様々な温度での圧力に対するZのグラフ（図1のような）を作成するために使用されるかもしれません。このようなグラフは、実験的に決定された値の間のZの補間値を容易に得るために有用である。

圧縮率は前述のように次のように表すこともできる：

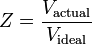
$Z = \frac{V_mathrm{actual}{V_mathrm{ideal}}$

圧縮率に影響を与える領域は3つある。

気体圧力が0に近づくとZの値は1になる傾向がある。すべての気体が理想的な振る舞いをする傾向がある場合
中間圧力では分子間引力によって実際の体積が理想値より小さくなるためZの値は1より小さくなり
Zの値は1より大きく、最終的には無限大となる傾向がある場合。高圧下では分子間反発力によって実際の体積が理想値より大きくなるため

純ガスの圧縮率グラフの一般化

圧縮率と還元温度との間には独特の関係があること。 Tr、および還元圧力Prは、1873年にファンデルワールスによって初めて認識され、対応状態の2パラメータ原理として知られています。対応状態の原理は、分子間力に依存する気体の性質は、気体の臨界特性に普遍的に関係するという一般論を表現したものである。気体の圧縮性に関しても、対応状態の原理から、同じ還元温度Tr、還元圧力Prの純粋気体は同じ圧縮率になるはずであることが示されている。

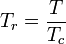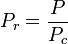
還元温度と圧力は次のように定義される。 $T_r = \frac{T}{T_c}$ , $P_r = \frac{P}{P_c}$

TcとPcは気体の限界温度と限界圧力として知られている。 Tcはある気体がそれ以上では液化できない温度、Pcはある気体がその臨界温度で液化するために必要な最小圧力で、それぞれ特定の気体の特性である。

実際の気体の圧力-体積-温度(PVT)データは、純粋な気体によってさまざまである。しかし、さまざまな単成分の気体の圧縮率を温度等温線とともに圧力に対してグラフにすると（図1下段のメタンのグラフのように）、多くのグラフは似たような等温線形状を示す。

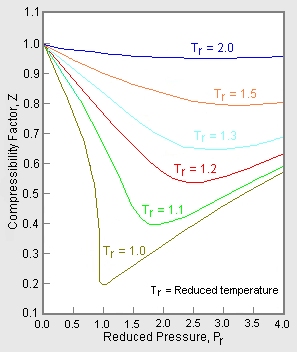
図2 一般化した圧縮率グラフの例

多くの異なるガスに対して使用できる一般化したグラフを得るために、圧縮率データの正規化に還元圧力と温度、PrとTrが使用されている。図2は、メタン、エタン、エチレン、プロパン、n-ブタン、i-ペンタン、n-ヘキサン、窒素、二酸化炭素、水蒸気の10種類の純ガスの数百のP-V-T実験データポイントから得られた一般化圧縮性係数グラフの一例である。

25種類以上の純ガスに基づく、より詳細な一般化圧縮率グラフ、例えばNelson-Obertグラフがある。このようなグラフは、Z値が0.6より大きい場合は1～2％以内、Z値が0.3～0.6の場合は4～6％以内の精度と言われている。

一般化圧縮率グラフは、正と負の電荷中心が一致していない気体である強極性気体ではかなりの誤差がある場合がある。このような場合、Zの推定値は15-20%程度の誤差が生じる可能性があります。

量子気体の水素、ヘリウム、ネオンは対応状態の振る舞いに従わないので、一般化グラフを用いた場合の圧縮率予測精度を上げるために、これら3気体の減圧と温度を以下のように再定義することが必要である。

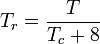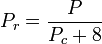
$T_r = \frac{T}{T_c + 8}$ and $P_r = \frac{P}{P_c + 8}$

where the temperature is in degrees Kelvin and the pressure is in atmospheres.

混合気体の一般化圧縮率グラフ

純粋気体の一般化圧縮率グラフ（図2やNelson-Obertグラフなど）は、W. B. Kayが1936年に提案したKayの法則を用いて混合気体にも用いることができる。この法則は、擬臨界温度Tpcと擬臨界圧力Ppcで定義される減温減圧時の混合気体の圧縮率を求めることにより、混合気体のP-V-T挙動を予測するもので、次のように定義される：

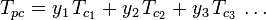
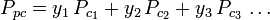
$T_{pc} = y_1,T_{c_1} + y_2,T_{c_2} + y_3} ,T_{c_3} ,\dots$ $P_{pc} = y_1,P_{c_1}. + y_2,P_{c_2} + y_3 },P_{c_3} ,\dots$

ここで。
Tpc	= 混合ガスの擬臨界温度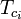
$T_{c_i}$	=混合ガス成分の臨界温度
Ppc	=仮臨界温度混合ガスの圧力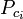
$P_{c_i}$	=ガスの成分の臨界温度
yi	=ガスの成分のモル（または容量）率

擬制温度.とする, 純ガスの一般化圧縮率グラフで使用するTprと擬似圧力Pprは次のようになります。

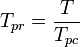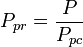
$T_{pr} = \frac{T}{T_{pc}}$ and $P_{pr} = \frac{P}{P_{pc}}$

天然ガス（炭化水素と他のガスの混合ガス）については、インターネット上で仮導入温度と圧力を用いた圧縮率グラフが公開されています。

The van der Waals equation

The van der Waals equationは1873年に開発され、次のように表されます：

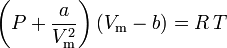
$P + \frac{a}{V_mathrm{m}^2}right)\left(V_mathrm{m} - bright) = R$

ここで。

aは気体分子間の引力の強さの尺度である bは気体分子によって占められる体積を説明し、利用可能な開放体積を減少させる

ファンデルワールス方程式は以下のように再整理することができる。

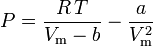
$P = \frac{R,T}{V_mathrm{m} - b} - \frac {a}{V_mathrm{m}^2}$

そして圧縮率も次のように書くことができる。

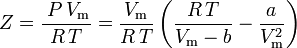
$Z = \frac{Thomas;P,V_mathrm{m}}{R,T} = \frac{V_mathrm{m}}{R,T}left(\frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2}right)$

ここでファンデルワールスのパラメータa、bを用いてZを求める式ができたことになります。

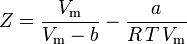
$Z = \frac{V_Cachemathrm}}{V_Cachemathrm} - b} - \frac{a}{R,T,V_Cachemathrm}}$

a、bは「ファンデルワールス定数」と呼ばれるが、気体によって異なるので真の定数ではなく、P、V、Tには無関係である。つまり、対象となる気体に対して一定である。ある気体の臨界温度と圧力が与えられたとき、その気体についてaとbは次の式から求めることができる：

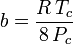
$a = \frac{27, R^2, T_c^2}{64, P_c}$ and $b = \frac{R, T_c}{8, P_c}$

例えば、エタンの臨界圧力を4としたとき.884MPa、臨界温度は305.43K(32.3˚C)である。気体定数Rを8.3145 Pa m3 K-1 mol-1とすると、a = 0.557 m6 Pa mol-2、b = 6.500×10-5 m3 mol-1が得られる。

van der Waals方程式の修正版

van der Waals状態方程式を用いて圧縮率を求めることは、一般化圧縮率表を用いるよりも改善された方法である。しかし、van der Waalsの状態方程式を改良して、さらに改良したものもある。石油精製、石油化学、天然ガス処理、低温蒸留などの技術者が最もよく使う状態方程式は、1949年に開発されたRedlich-Kwong方程式、1972年に開発されたSoave-Redlich-Kwong方程式、1976年開発のPeng-Robinson方程式であろう。この3つの方程式は、基本的にファンデルワールス方程式を修正したものである。比較のための方程式は

Redlich-Kwong

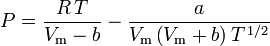
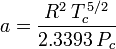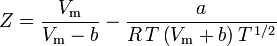
$P = \frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}left(V_mathrm {m} + bright)T^{,1/2}}$ $a = \frac{R^2 ◇, T_c^{}{2.5/2}}{2.3393, P_c}$ and $b = \frac{R}, T_c}{11.5420, P_c}$ $Z = \frac{V_myatrm{m}}{V_myatrm{m} - b} - \frac{a}{Renta, Tentaleft(V_myatrm {m} + bentaright)T^{},1/2}$

Soave-Redlich-Kwong

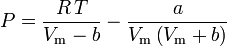
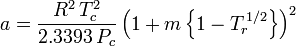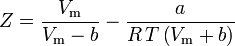
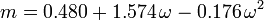
$P = \frac{R,T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}left(V_mathrm {m} + bright)}$ $a = \frac{R^2,T_c^2}{2.3393,P_c}, \Big(1 + m}, \Big{1 - T_r^{C},1/2} ³)^2$ and $b = \frac{R³,T_c}{11.5420, P_c}$ $Z = \frac{V_arettemathrm{m}}{V_arettemathrm{m} - b} - \frac{a}{R, Taretteleft(V_arettemathrm {m} + baretteright)}$ $m = 0.480 + 1.574, \omega - 0.176, \omega^2$

Soave-Redlich-Kwong, Peng-Robinson equationsのパラメータとして用いられるacentric factor、ωは1955年にPitzerらによって初めて導入された。これは次のように表される：

mega = \log_{10} \ここでPvpは 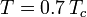$T = 0.7</span>、T_c$ の温度における気体の飽和蒸気圧を表す。

Peng-Robinson

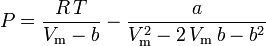
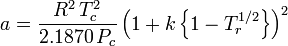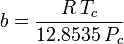$P = \frac{R},T}{V_mathrm{m} - b} - \frac{a}{V_mathrm{m}^2 - 2\,V_mathrm{m}, b - b^2}$ $a = ⒜frac{R^2,T_c^2}{2.1870,P_c}, \Big(1 + k}, \Big{1 - T_r^{1/2} \Big})^2$ and $b = \frac{R, T_c}{12.8535}, P_c}$ Z = \frac{V_mathrm}{V_mathrm} – b} – \frac{a}{R,T,V_mathrm{m} } {R,T, V_mathrm{m}} {V, T, V_mathrm{m}} – b} B = \frac{V_mathrm{m}} {V, T, V_mathrm{m} {V, T, V_mathrm{m} } {V, T, V_mathrm{m}} – b} Z = \frac{V, T + 2,Rgeant,Tgeant,b – \left(Rgeant,Tgeant, b^2/V_mathrm{m}) }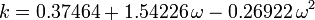 $k = 0.37464 + 1.54226, \omega - 0.26922, \omega^2$

Virial equation of state

The most fundamental equation of state , which has most sound theoretical found that is Virial equation of state:

◇Phrac{P},V_mathrm{m}}{R},T} = Z = 1 + ◇V_mathrm{m}} ◇Phrac{B}{V_mathrm{m}} ◇Phrac{B}{V_mathrm{m}}{R} = Z = 0 + 0 + \frac{C}{V_mathrm{m}^2} + \frac{D}{V_mathrm{m}^3}. + 1885年にThiesenが経験則に基づいて提案し、1901年にKamerlingh-Onnesがさらに発展させたものです。 Bの統計力学的な式はOrnsteinが博士論文で初めて導出した。その後、1927年にH.D.Ursellによって、分子間力の統計力学的（クラスター）分析から導かれた理論に基づいて、この式が再定義された。この係数は気体によって、また対象とする気体の温度によって変化するので、定数ではない。また、温度の関数であることを示すために、B(T)、C(T)、D(T)と表記することもある。係数の数値は実験的に決定する必要がある。

気体の非理想的な振る舞いの補正は、2番目のビリアル係数が最も大きな部分を占めます。そのため、ビリアル方程式は2番目の係数を含む項の後で切り捨てられることがある。しかし、3番目の係数がある場合は、3番目の係数を含む項で切り捨てるのが一般的である。 3632>

以前はテキサス A&M 大学、カレッジステーション、テキサス州にあり、現在はコロラド州ボルダーの国立標準技術研究所 (NIST) にある熱力学研究センターのビリアル係数データベースから、純ガスおよび混合ガスに対するビリアル係数の幅広い編集が作成されました。その最新版は2003年に出版された。 NISTはまた、NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) というソフトウェアも販売しており、第2、第3ビリアル係数や他の多くの熱力学的特性も収録している。おそらく最もよく知られているのは、1929年に開発されたBeattie-Bridgeman方程式と1940年に開発されたBenedict-Rubin-Webb方程式であろう。一般に、これらの式は上で述べた式よりも複雑である。

気体定数の表記

この記事で用いる気体定数は、あらゆる気体に適用される普遍気体定数Rである。また、気体定数にはRsと表記できる比気体定数があり、Rs=R/M(Mは分子量)で定義される。

残念なことに、技術文献の多くの著者は、Rを比気体定数と表記せず、また比気体定数であることを明記せずに使っていることがあります。これは混乱を招きかねない。

1.0 1.1 1.2 1.3 1.4 McQuarrie, Donald A. and Simon, John D. (1999). 分子熱力学(Molecular Thermodynamics). ユニバーシティ・サイエンス・ブックス. ISBN 1-891389-05-x.
2.0 2.1 2.2 2.3 2.4 Yunus A. Çengal and Robert H. Turner (2004).分子熱力学. 熱流体科学の基礎、第2版。 McGraw-Hill Professional. ISBN 0-07-245426-1.
3.0 3.1 3.2 3.3 3.4 Smith, J.M.他 (2005). 化学工学熱力学入門、第7版。 McGraw Hill. ISBN 0-07-310445-0.
4.0 4.1 4.2 4.3 4.4 4.5 4.6 Y.V.C. Rao (1997). 化学工学熱力学. Universities Press (インド). ISBN 81-7371-048-1.
5.0 5.1 気体の法則（カナダ・クイーンズ大学 M.J. Mombourquette 教授による講義）
Hong Wei Xiang (2005). 対応状態原理とその実践。流体の熱力学、輸送、表面物性。 Elsevier. ISBN 0-444-52062-7.
IUPAC Goldbook
Gouq-Jen Su (1946年). “対応する状態の修正された法則”。工業 & 工学化学 38 (8): 803-806. issn 0096-4484.
9.0 9.1 状態方程式（カナダ・コンコルディア大学 Lyes Kadem 教授）
10.0 10.1 状態方程式（米国・ウィスコンシン大学 Sanford Klein 教授使用講義資料）
Richard W. Miller（1996). 流量計測工学ハンドブック第3版. マグロウヒル社。 ISBN 0-07-042366-0. (G.145ページの図G-1参照)
Kai-Fui Vincent Wong (2000). エンジニアのための熱力学、第1版。 CRCプレス. ISBN 0-8493-0232-3。 (図 A-2, 278 ページ参照）
Nelson-Obert Generalized Compressibility Charts (Charts available on the Internet, from the website of San Diego State University, U.S.)
W.B.Kay (1936). 「高温高圧下の気体・蒸気-炭化水素の密度”. 経営工学 & 化学 28:1014. ISSN 0096-4484.
Yunus A. Çengal and Michael A. Bowes (2005). 熱力学: An Engineering Approach, 5th Edition. McGraw-Hill. ISBN 0-07-2884959.
Real Gases (Professor R.M. Price at Christian Brothers University, U.S.A.)
Properties of Natural Gases (Professor Jon Steiner Gudmandsson, Norwegian University of Science and Technology)
Robert C. Weast (Editor) (1975). 化学と物理のハンドブック第56版. CRC Press. ISBN 0-87819-455-x.
19.0 19.1 19.2 Chapter 3: Equations of State (pages 6-8 of 65 pdf pages) (Part of the PhDsis by Ji Lin Wang, 2002, Swinbourne University of Technology, Australia)
20.0 20.1 20.2 ジャン・ヴィダル(2003). 熱力学: 熱力学：化学工学と石油産業における応用. Editions Technip. ISBN 2-7108-0800-5.
Zakia Nasri and Housam Binous (2007). “Mathematicaを用いたSoave-Redlich-Kwong状態方程式の応用”. 化学工学論文集 40 (6): 534-538. ここから取得。
K.S. Pitzer et al (1955). “The Volumetric and Thermodynamic Properties of Fluids”（流体の体積および熱力学的特性）。アメリカ化学会誌 77: 3427-3440.
フランシス・S・マニング、リチャード・E・トンプソン(1991). 石油の油田処理. ペン・ウェル・ブックス. ISBN 0-87814-343-2.
Acentric Factor Definition (Physical Property Sources Index, PPSI, of the Swiss Federal Institute of Technology Zurich)
Max F.. Thiesen (1885)。 “Investigations of the Equation of State”. Annalen der Physik und Chemie (24): 467-492.
Heike Kamerlingh-Onnes (1901)。「気体および液体の状態方程式の直列による表現”. Commun. Phys. Lab. Leiden (71).
S. L. Ornstein (1908) Toepassing der statistische mechanica van Gibbs op molekulair-theoretische vraagstukken (Application of the statistical mechanics of Gibbs on molecular-theoretische issues), Leiden
H. D. Ursell (1927)． “不完全気体に対するGibbsの相積分の評価” (23): 685.
J.D. Dymond and R.C. Wilhoit (Authors), K.N. Marsch and M. Fenkel (Editors) (2003). 純粋気体および混合気体のビリアル係数、第1版。 Springer. ISBN 3-540-44340-1.
NIST Standard Reference Database 23
J.A. Beattie and O.C. Bridgeman (1929).の項参照。 “A New Equation of State for Fluids”（流体の新しい状態方程式）。 Proc. Amer. Acad. Arts Sci. (63): 229-305.
M. Benedict, G.B. Webb and L.C. Rubin (1940). 「軽質炭化水素とその混合物の熱力学的性質に関する経験式”(An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures). J. Chem. Phys. 8: 334-335.

このページの内容の一部は、以前に Citizendium.

“http://knowino.org/wiki/Compressibility_factor_(gases)”

カテゴリーから取得したものです。物理学

目次