混同行列の用語の簡単なガイド

by

混同行列は、真値がわかっているテストデータの集合に対する分類モデル（または「分類器」）の性能を説明するためによく使用される表です。 混同行列自体は比較的簡単に理解できますが、関連する用語は混乱することがあります。

私が混同行列用語の「クイック リファレンス ガイド」を作成したいと思ったのは、既存のリソースで、表示がコンパクトで、任意の変数ではなく数値を使用し、数式と文章の両方で説明するという私の要求に合うものが見つからなかったからです。

まず、2 値分類器の混同行列の例から始めましょう (ただし、2 つ以上のクラスがある場合に簡単に拡張できます):

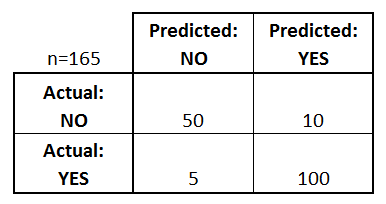
Example confusion matrix for a binary classifier

この行列から何がわかるか？

  • There are two possible predicted classes: “yes “と “no “です。 例えば病気の有無を予測する場合、「はい」はその病気を持っていることを意味し、「いいえ」はその病気を持っていないことを意味します。
  • 分類器は合計165の予測を行いました（例．
  • その165件のうち、分類器は110回「はい」と予測し、55回「いいえ」と予測しました。
  • 実際には、サンプルの105人の患者がその病気を持っており、60人の患者が持っていません。

ここで、最も基本的な用語を定義しましょう。

  • 真陰性（TN）：私たちが「はい（病気を持っている）」と予測し、実際に病気を持っているケースです。 偽陽性(FP)：「いいえ」と予測したが、実際には病気ではなかった場合。 Yesと予測したが、実際には発症していない。 (「タイプIエラー」とも呼ばれる)
  • 偽陰性(FN): 私たちは「いいえ」と予測したが、実際には病気を持っていた。 (「II型エラー」とも呼ばれる)

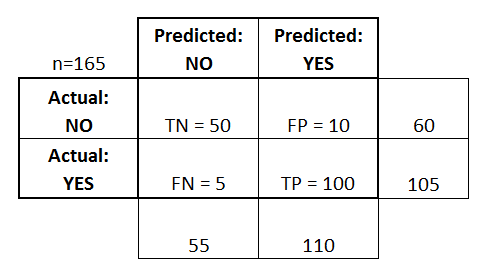
    • これらの用語を混同行列に追加し、行と列の合計も追加しました：

    Example confusion matrix for a binary classifier

    This is a list of rate that are often computed from a confusion matrix for a binary classifier:

    • Accuracy.This は、2つの分類器の混乱行列から計算することができる率のリストです。 全体として、分類器はどれくらいの頻度で正しいか？
      • (TP+TN)/total = (100+50)/165 = 0.91
    • 誤判定率：分類器の誤判定率。
      • (FP+FN)/total = (10+5)/165 = 0.09
      • 1マイナス精度
      • 別名「エラー率」
    • True Positive Rate（真陽性率）：全体としてどれくらいの頻度で間違っているのか。
      • TP/actual yes = 100/105 = 0.95
      • またの名を「感度」または「再現率」
    • False Positive Rate（誤検出率）：実際にYesの場合、何回Yesを予測するか。
      • FP/actual no = 10/60 = 0.17
    • True Negative Rate（偽陽性率）：実際にノーだった場合、どれくらいの確率でイエスを予測できるのか？ 7270>
    • TN/actual no = 50/60 = 0.83
    • 1マイナスFalse Positive Rateに相当
    • 別名：Specificity
  • Precision。 7270>
  • TP/predicted yes = 100/110 = 0.91
  • Prevalence（有病率）：Yesと予測したとき、どれくらいの確率で正しいか。
    • actual yes/total = 105/165 = 0.64

    他のいくつかの用語も言及する価値があります：

    • Null Error Rate（ヌルエラー率）。 これは、常に多数派クラスを予測した場合に、どれくらいの確率で間違うかを示しています。 (この例では、常に「はい」と予測した場合、60件の「いいえ」に対してのみ間違うので、ヌルエラーレートは 60/165=0.36 となる)。 これは、分類器を比較するためのベースライン指標として有用です。
    • Cohen’s Kappa: これは本質的に，分類器が偶然にどれだけよく機能したかと比較して，どれだけよく機能したかを示す尺度である． 言い換えれば，精度とヌル誤り率の間に大きな差がある場合，モデルは高いカッパ・スコアを持つことになる． (コーエンのカッパの詳細。)
    • F スコア。 真陽性率(recall)と精度の加重平均値です。 (Fスコアの詳細)
    • ROC曲線(ROC Curve)。 これは一般的に使用されるグラフで、すべての可能な閾値における分類器の性能を要約したものです。 これは，与えられたクラスにオブザベーションを割り当てるためのしきい値を変化させながら，偽陽性率（x軸）に対する真陽性率（y軸）をプロットすることによって生成される． (ROC カーブの詳細)

    そして最後に、ベイズ統計学の世界の人のために、Applied Predictive Modeling からこれらの用語を簡単にまとめます：

    ベイズ統計学に関連して、感度と特異度は条件付き確率、優勢は事前、陽性/陰性の予測値は事後確率となります。

    もっと学びたい？

    35 分の新しいビデオ「Making sense of the confusion matrix」では、これらの概念をより深く説明し、より高度なトピックを取り上げています。

    • 多クラス問題の精度とリコールの計算方法
    • 10クラスの混同行列の分析方法
    • 問題に適した評価メトリックの選択方法
    • なぜ精度がしばしば誤解を招くメトリックであるか

    ご質問があれば教えてください!

    • コメントする